C
calculate
To find an answer using math operations (addition, subtraction, multiplication or division).
page 369
capacity
The volume of the inside of a container.
Cartesian coordinate system
A method of locating points on a flat surface by means of numbers. This method is named after its originator, René Descartes.
(See also coordinates.)
pages 324–326, 340
centimeter (cm)
A unit of measure in the metric system. A centimeter is 
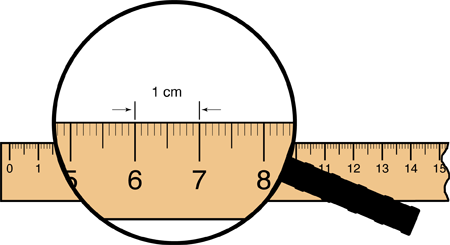
pages 100, 111–112, 121, 129–130, 340
certain event
Something you know will definitely happen.
page 11
clock face
The part of the clock that shows the numbers for the hours and the minutes.
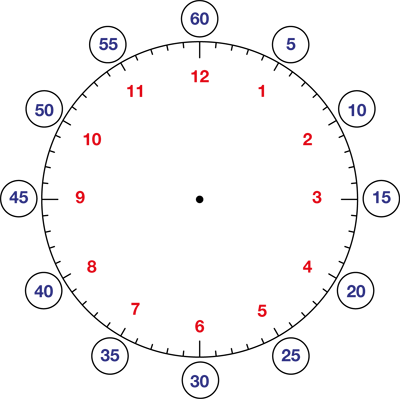
pages 55, 96–98, 150–152, 195, 300–301
column
In an array, the objects lined up vertically (up-down).

pages 34, 38, 39, 43, 44, 129, 138, 142, 161, 354
common fraction
Any fraction that is written with a numerator and denominator that are whole numbers. For example, 

(See also fraction and decimal fraction.)
commutative property
(of addition) Changing the addends does not change the sum. For example, 3 + 5 = 5 + 3.
(of multiplication) Changing the order of the factors does not change the product. For example, 3 × 5 = 5 × 3.
This is also known as the Order Property.
compact method
A method of problem solving by calculating one column at a time, starting on the right, and making trades.

pages 142–145
cone
Shapes with a base and all points on the base connect to a top vertex or apex. The base may be any shape. Using this definition, all pyramids are special cones. A circular cone has a base in the shape of a circle.

pages 318, 321, 322
congruent
Shapes with the same shape and size. Shapes are congruent if you can place one shape so it fits on top of the other and they match exactly.

pages 308, 318, 321, 322
constant
Always the same.
pages 196–198, 232–233, 284–286
constant hopper
A mathhopper that always makes the same size hops on a number line.
(See also mathhoppers.)

pages 196–198, 232–233, 284–286
convenient number
A number used in computation that is close enough to give a good estimate but is also easy to compute mentally (e.g., 25 and 30 are convenient numbers for 27).
(See also benchmark numbers and friendly numbers.)
pages 243, 351, 352
coordinates
An ordered pair of numbers that indicate the position of a point on a flat surface by giving distances from a pair of coordinate axes. For example, if a point has coordinates (8, 3) it is 8 units from the vertical axis and 3 units from the horizontal axis.
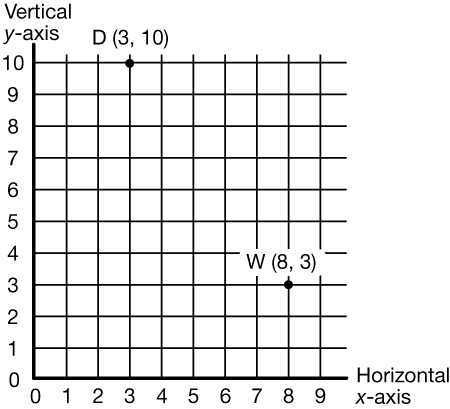
pages 324–326, 340
counting back
A subtraction strategy in which students start from a larger number and then count down the smaller number until they reach the difference. For example, to solve 8 − 3, begin with 8 and count down three: 7, 6, 5. Another example:
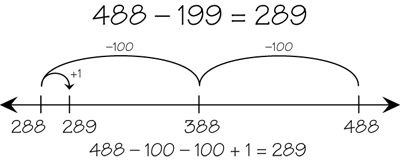
page 152
counting down
(See counting back.)
counting on
An addition strategy in which students start at one number and count forward the value of the second number to find the total.
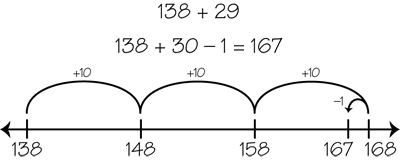
page 166
counting up
A subtraction strategy in which students start at the lower number and count on to the higher number. For example, to solve 8 − 5, start at 5 and count up three: 6, 7, 8. So 8 − 5 = 3. Another example:
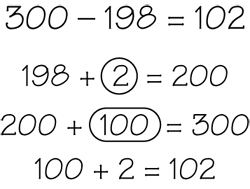
cube
A three-dimensional shape with six congruent square faces.

pages 314, 319–320
cubic centimeter (cc)
The volume of a cube that is one centimeter on each edge.
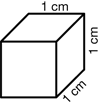
pages 401, 402–404, 409, 411–412
cup
A unit of volume equal to 8 fluid ounces; one-half pint.
page 283
cylinder
A three-dimensional shape with two congruent and parallel faces. Lines joining the corresponding points on the two bases are always parallel. All prisms are special kinds of cylinders. A circular cylinder has two congruent and parallel circles as bases.
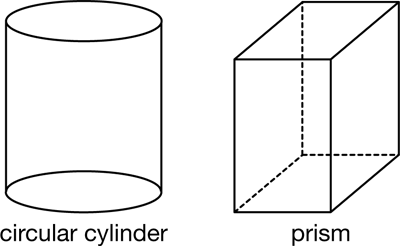
pages 315, 318










