Use Question 11 to summarize the lesson. In this question, students compare additive growth to the growth of a square. In Questions 11A and 11B, students compare the new growth (G) to the size of
the turtle (S). For each data point (except the first one), the size is greater than the new growth. In Question 11C students explore “by how much?”
Begin a discussion by asking:
- Which quantity grows more quickly—the new growth in squares (G) or the size in squares (S)? (The size in squares (S) grows more quickly.)
- How can you tell? (Possible response: The difference between S and G keeps getting larger; the growth (G) increases by the same number, 2 squares for each year, whereas the size S increases by larger numbers of squares each year.)
- How can you use your graphs to show which quantity grows more quickly? (The straight line has the same steepness all the time, but the curve starts out almost flat and then gets very steep quickly. That shows that Size grows more and more rapidly each year.)
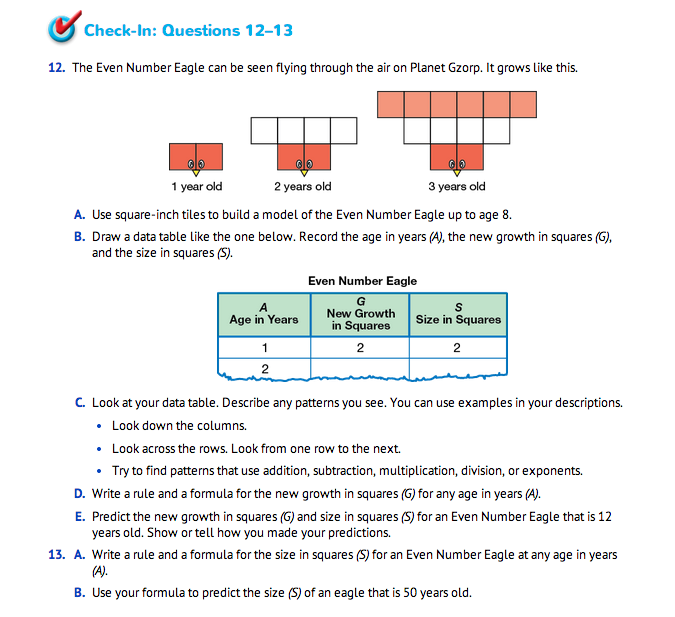
Assign Check-In: Questions 12–13 for students to complete independently.
Use students' responses to Check-In: Questions 12–13 on the Square Number Patterns page in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to identify and describe number patterns [E3]; use variables in formulas to represent number patterns and make predictions [E4]; represent number patterns using words, tables, and graphs [E8]; and make predictions and generalizations using data tables and graphs [E9].
For Question 13, students write a rule in words and a formula for finding the size in squares (S) at any age in (A) for the Even Number Eagle.
Have students propose different rules and post these on a display. Then have other students test the rules.
- How did you use the different operations to look for a formula? addition? subtraction? multiplication? division?
- How did you use exponents to look for a formula?