Classify Numbers

Review Terms. Number Bingo is a game that requires students to classify numbers as odd, even, prime, composite, square, cubic, or as a multiple of 3. It also provides a context for discussing solution strategies. Analyzing the game boards that are most likely to win gives students an opportunity to apply what they have learned about categorizing numbers.

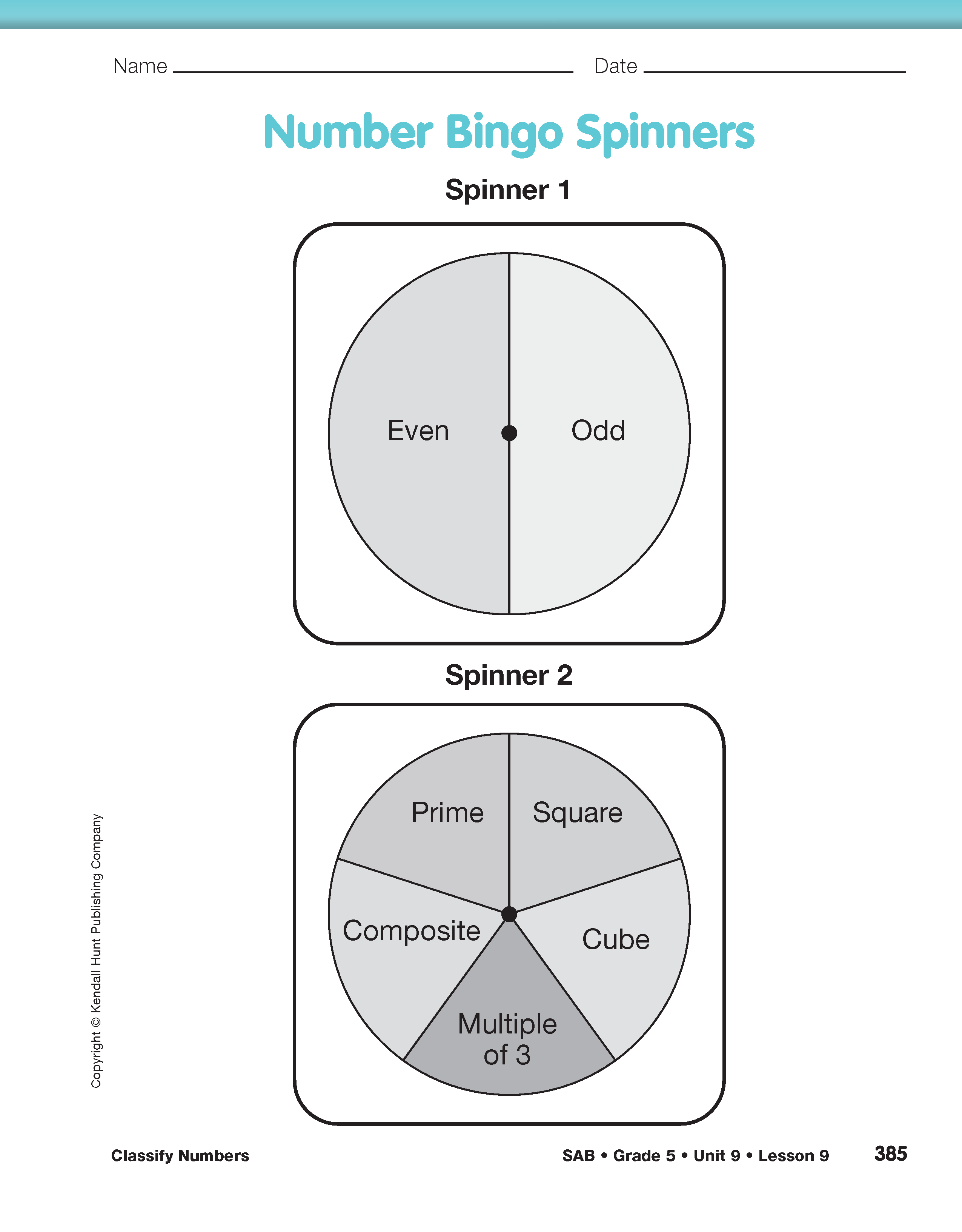
There are two spinners for this game on the Number Bingo Spinners page in the Student Activity Book. Before playing the game, it may be helpful to review each of the terms that appear on Spinner 2.

Play Number Bingo. Begin by discussing the rules for Number Bingo on the Classify Numbers pages in the Student Guide.

• Each group of five students selects a Caller who will spin the spinners and call out the categories.
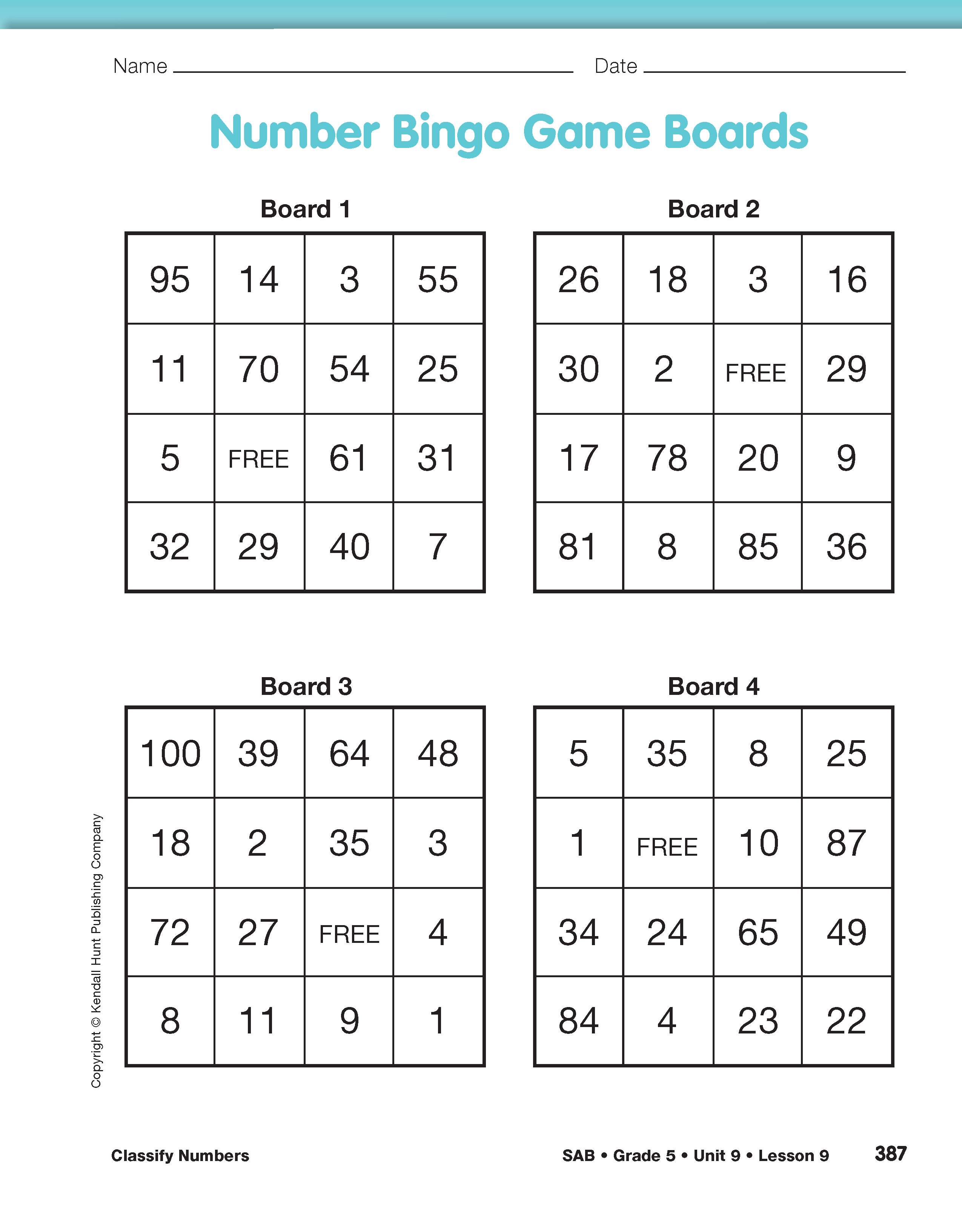
• The four remaining students choose a game board on the Number Bingo Game Boards page in the Student Activity Book. Each player must select a different game board.
• Players place a marker on the space marked “FREE” on the game board.
• Each player tries to find a number that matches both categories spun by the Caller.
• If a player finds any numbers that match, the player places a marker on one of those numbers. Players mark only one number for each spin, even if more than one number on the board matches the spin.
• The Caller keeps a list of the categories spun for each turn.
• The first player to get four markers in a row (horizontally, vertically, or diagonally) or a marker in each corner is the winner.
• The Caller checks to make sure that each of the winner's numbers matches one of the turns recorded on the record sheet.

Ask students to play Number Bingo for 20 minutes. If they finish a game before that time, they may start another game with a different student acting as the Caller and the players selecting a board other than the one they played in the previous game. Ask the Caller to record which game board won in each game.

The questions in the Student Guide help guide a discussion of the number categories and game strategies. Students answer the questions by comparing all four boards.

Overall, Board 3 is the best board because it has the most numbers that fit into more than one category. For example, 64 is a square number (8²), a cube (4³), and a composite number. The number 27 is a cube, a composite number, and a multiple of 3. Of the 15 numbers on Board 3, all but three of them (2, 11, and 35) fit into more than one category on Spinner 2.

Board 1, on the other hand, is the weakest board because the majority of its numbers fit into only a single category (either prime or composite, but no others) of Spinner 2. Boards 2 and 4 contain a mix of single-category and multiple-category numbers.

Give students a few minutes to discuss Questions 1–6 in small groups. Pay attention to the discussions of students in their small groups.

Then ask students to pool the results of which boards won and display the class totals on a display. It would be expected that the results would show that the answer to Question 1 is Board 3 and the answer to Question 2 is Board 1. Because the outcome is based on probability, however, this outcome is likely, but not certain. An outcome that does not match what is expected can launch a rich discussion in the classroom about the uncertainty of outcomes.

For Questions 5 and 6 students consider which numbers will be spun most often and least often, respectively.