Throughout the unit, students find factors and multiples of numbers. Finding factors and multiples helps them classify a number as prime or composite, make generalizations about a number, and find rules for describing numerical patterns.

The factorization of a number places the number into one of two fundamental categories of numbers: prime and composite. Composite numbers have more than two distinct factors (e.g., 6 is a composite number, since it has four distinct factors: 1, 2, 3, and 6). Prime numbers, on the other hand, have exactly two distinct factors: 1 and the number itself.

The prime numbers are the building blocks of all the counting numbers, since all counting numbers are either prime or can be expressed as a product of prime numbers. Such a product is called the prime factorization of the number. For example, the prime factorization of 28 is 2 × 2 × 7 or, with exponents, 2² × 7. In this unit, students investigate how to find and identify prime numbers. They decompose numbers down to the building blocks of their prime factors and look for patterns in prime numbers.

In Lesson 9, students explore a basic system of classifying numbers. The idea of classification in mathematics has already been addressed with regard to geometric shapes in Unit 6. In this unit, students classify numbers based on number properties such as divisibility, number of factors, and whether numbers are squares, cubes, even, odd, prime, or composite. Students use diagrams to organize numbers into these categories (and combinations of these categories) based on their properties.

The investigations in Lessons 3 and 4 build on the early algebra strand that develops throughout the Math Trailblazers curriculum. In these lessons, students investigate patterns of numerical growth. They identify patterns and describe the numerical relationships using words and formulas.

This focus on early algebraic thinking is developed throughout Math Trailblazers. Following recommendations of researchers, activities that give students concepts and skills needed to make a natural transition from learning and doing arithmetic to learning and doing algebra are integrated throughout all grades (Carpenter et al., 2003; Carraher and Schliemann, 2007; Kaput, 2008; Kilpatrick and Izsak, 2008; Schliemann et al., 2007). Students extend and connect their concepts of number, geometry, measurement, and data to develop tools for algebraic reasoning. These tools enable them to “do algebra,” that is, to identify, describe, and visualize patterns and relationships. They learn to make generalizations about numbers that are collected in data sets, organized in tables, and pictured in graphs.

Many of the number patterns students have studied in Math Trailblazers came from data measured in laboratory investigations. In this unit, students study patterns in sequences of whole numbers rather than relationships between measured variables. Students examine these patterns to look for a rule that describes them, using tables and graphs as tools. Figure 1 shows an example of such a pattern for the growth of an imaginary animal modeled with square tiles.

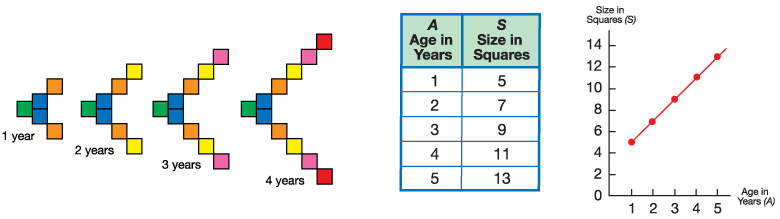
Figure 1: A constant growth pattern represented by tiles, a table, and a graph

When investigating sequences of numbers such as that shown in the table in Figure 1, there are several patterns to notice. Looking down the columns, one notices that the Age in Years (A) and the Size in Squares (S) both increase consistently for each successive row, by one year in the first column and by two squares in the second. Looking across the rows, the relationship between the numbers may be more challenging to find. In this case, the size (S) is always double the value of the age (A) plus 3, or written as a formula:

S = 2 × A + 3

Students will investigate the patterns found in these relationships and draw connections between their various representations: pictures, tables, rules, formulas, and graphs. The ability to model a situation mathematically not only allows students to make predictions about values of variables, it also builds the habits of mind needed to solve increasingly complex mathematical problems that occur in the real world. Students will use mathematical models to make generalizations and predictions about the patterns they discover.

A particularly important property of a numerical pattern is found in the way that a pattern grows. Some patterns grow at a constant rate; others do not. In constant growth patterns, such as the one shown in Figure 1, the growth is the same over each unit of time (e.g., two squares are added for every year of growth). In Lesson 4, students investigate a pattern that is based on the square numbers. Such a pattern does not demonstrate constant growth because the same number of squares are not added for each unit of time. In this case, the number of squares added increases each year. See Figure 2. Students will compare these different types of growth by comparing the models they use to represent them.

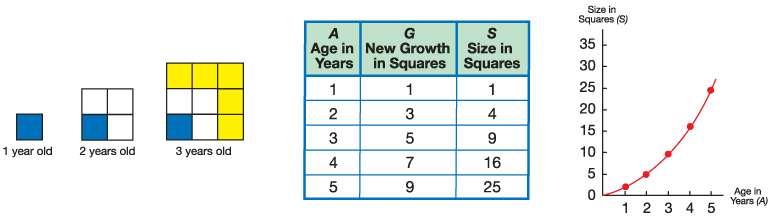
Figure 2: A square growth pattern represented by tiles, a table, and a graph

Resources

• Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically. Heinemann, Portsmouth, NH, 2003.
• Carraher, David W., and Analucia D. Schliemann. “Early Algebra.” In Second Research Handbook on Mathematics Teaching and Learning, pp. 669–706. Frank K. Lester, Jr., ed. National Council of Teachers of Mathematics, Reston, VA, 2007.
• Cuevas, G.J., and Karol Yeatts. Navigating Through Algebra in Grades 3–5. National Council of Teachers of Mathematics, Reston, VA, 2001.
• Eves, H. An Introduction to the History of Mathematics. Holt, Rinehart and Winston, New York, 1969.
• Greens, C.E. and R. Rubenstein, eds. Algebra and Algebraic Thinking in School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2008.
• Kaput, J.J. Algebra in the Early Grades. Lawrence Erlbaum Associates, New York, NY, 2008.
• Kilpatrick, J., and A. Izsak. “A History of Algebra In the School Curriculum.” Algebra and Algebraic Thinking in School Mathematics. C.E. Greens and R. Rubenstein, eds. National Council of Teachers of Mathematics, Reston, VA, 2008.
• Schliemann, A.D., D.W. Carraher, and B.M. Brizuela. Bringing Out the Algebraic Character of Arithmetic. Lawrence Erlbaum Associates, Mahwah, NJ, 2007.
• Serifina, R., E. Cann, D. Lavoie. “Prime Number Chart.” Teaching Children Mathematics, pp. 203–204, 1995.
• Sowder, J. “Estimation and Number Sense.” In Handbook of Research on Mathematics Teaching and Learning, pp. 371–389. D.A. Grouws, ed. Macmillan Publishing Company, New York, 1992.
• Tahan, M. (translated by L. Clark and A. Reid). The Man Who Counted. W.W. Norton & Company, Inc., New York, 1993.