Sink and Float

Est. Class Sessions: 3

Developing the Lesson

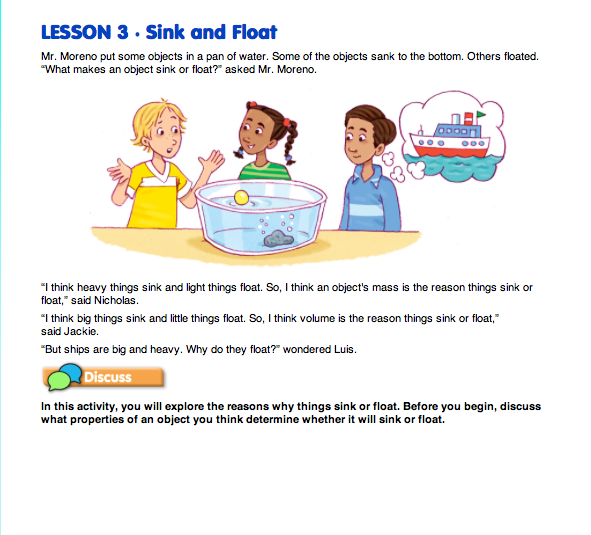
Reflect on the Properties of Objects that Sink and Float. Read together the opening vignette in the Sink and Float pages in the Student Guide.

Ask students these or similar questions:

What are some objects that float? (Possible responses: boats, surf boards, life preservers, apples, leaves, bath toys, feathers)
What are some objects that sink? (Possible responses: ship anchors, cement blocks, stones, marbles, coins, silverware)
Can you think of some instances where an object that usually floats would sink? (Possible responses: Fill a boat with water, put marbles in a paper cup, take the air out of an inner tube, or hold a piece of cardboard underwater until it's soaked.)
Can you think of some instances where an object that usually sinks would float? (Possible responses: Put a penny on a dry sponge, change a clay ball into a clay bowl, blow air into a plastic raft, or put a brick in a row boat.)
Why do you think things sink and float? What properties should we look at to determine what makes objects sink and float? (Possible responses: size, shape, weight, volume, and mass)

Tell students they will explore these properties by finding the mass and volume of objects and looking for patterns that predict whether the objects will sink or float.

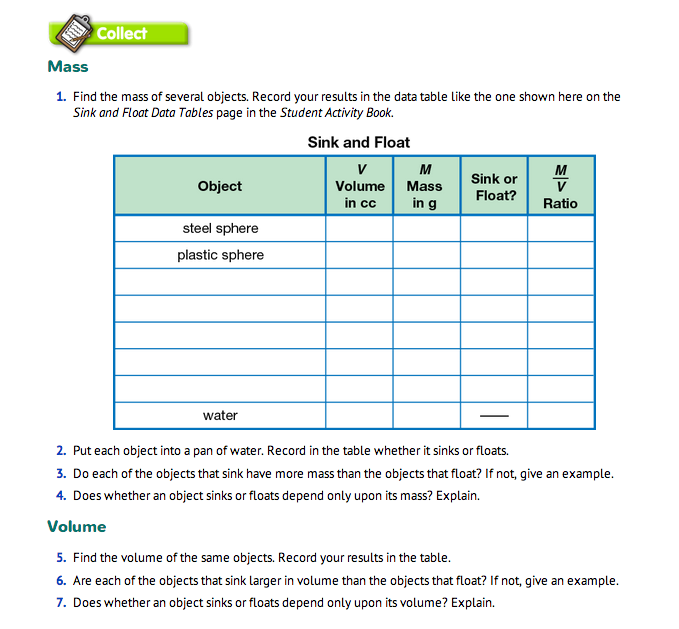
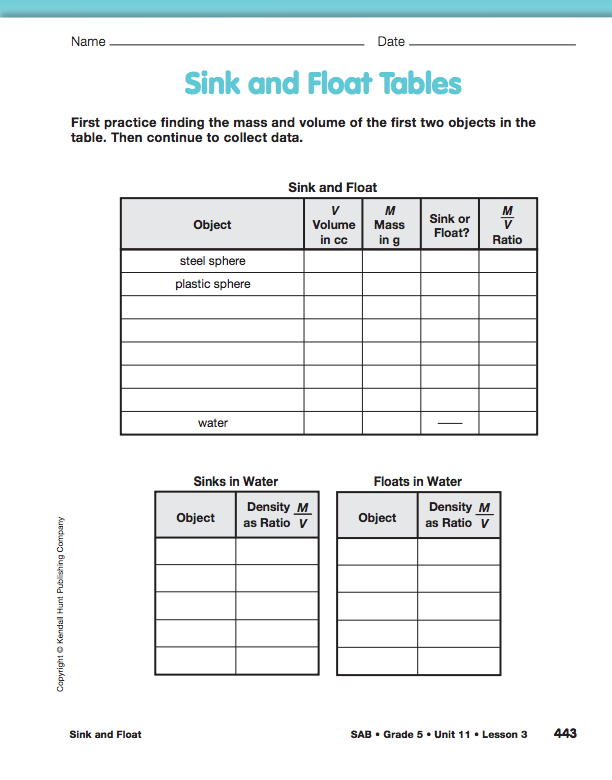
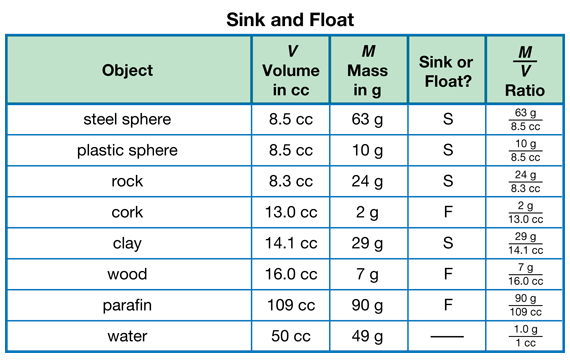
Observe Mass and Volume Measurement. Provide each student pair with a two-pan balance, gram masses, graduated cylinder, cup of water, towels, eyedropper, dishpan of water, and objects to investigate. See Materials Preparation. In order to find out what the students already know about finding mass and volume, observe them as they collect the mass and volume data for the first two objects only as presented in Question 1. Display and ask students to record their data on the Sink and Float Data Tables page in the Student Activity Book. Sample data are displayed in Figure 2.

Share Measurement Guidelines. After students have tried to find the mass and volume of the first 2 items, bring the class together. Create a list of reminders to keep posted throughout the investigation.

Ask students:

What do you have to remember to do to find the mass? (Possible responses: Use a piece of clay to zero the balance; leave the gram masses together and only take out the smaller ones; keep the table steady and try not to bump or shake it; double-check that the gram masses were counted correctly.)
How do you know which side of the scale has more mass? (Possible responses: It goes down. The side with more mass goes down.)
What do you have to remember when measuring volume by displacement? (See Figure 3.)
If an object floats, how do you get it below the surface? (Possible response: Use a pencil point to push the object down and hold it under water.)
How could you double-check the reasonableness of the volume measurement? (Possible response: Estimate the volume by making a model of the object with centimeter connecting cubes and count the cubes. Compare this volume measurement with the volume found through displacement.)

Terminology for Weight and Mass. Math Trailblazers encourages students to use familiar language when dealing with mass. For example, students may say that they are “weighing” objects instead of finding the mass. Traditionally, we use a two-pan balance to find the mass of an object and a spring scale (e.g., a bathroom scale) to weigh an object. Mass is the amount of matter in an object and weight is a measure of the pull of gravity on the object.

Provide Guidance on Measuring the Paraffin Block and Mass and Volume of Water. The paraffin block won't fit in the graduated cylinder, so its volume will have to be measured another way. One way is to measure the dimensions of the block and then compute its volume on a calculator by multiplying length × width × height. The block used in the sample data had dimensions 12.6 cm × 6.2 cm × 1.4 cm and a volume of approximately 109 cc. Students should measure the block's length, width, and height to the nearest tenth of a centimeter. Because of irregularities in the block and the fact that we are multiplying approximations (in length, width, and height), the final result for the volume of the block may not be very accurate.

Guide students to find the mass and volume of water by following these steps:

Find the mass of the empty graduated cylinder in grams and write it down.
Pour 50 cc of water into the graduated cylinder, using an eyedropper to put in the last few drops for accuracy. Check that the meniscus is right at the 50-cc mark.
Put the graduated cylinder filled with 50 cc of water on the scale and measure the mass.
Subtract the mass of the empty graduated cylinder to find the mass of the water.

If students need a more intensive review, display the Mass Review and Volume Review Masters in the Teacher Guide and go over the steps together.

Continue Mass and Volume Data Collections. Have student pairs continue to measure the mass and volume of the objects on their own and record their measurements on the Sink and Float data table. In Questions 1–4, students measure the mass of several objects and observe that mass alone does not determine whether an object will sink or float. In Questions 5–7, they measure the volume of the same objects and observe that volume alone does not determine whether an object will sink or float. Circulate the room to observe and support student investigation.

By collecting data, students will observe that sinking and floating do not depend only on mass or only on volume. After students have completed Questions 1–7, ask students again what properties they think determine whether an object will sink or float. In the discussion, they might suggest that sinking and floating have something to do with both mass and volume.

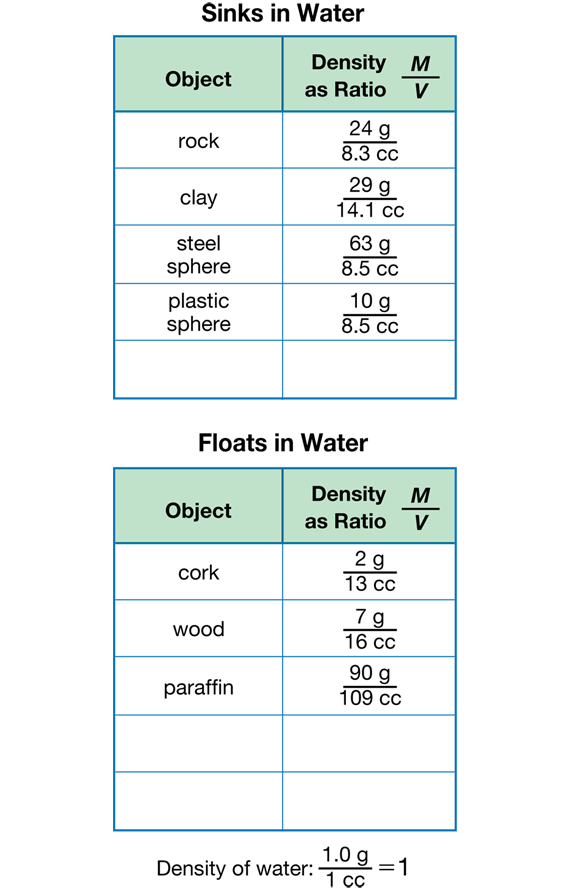
Density of Water. Students measure the volume and mass of water in Questions 1 and 5. When the metric system was developed, the gram was defined to be the mass of 1 cubic centimeter of water (at standard temperature and air pressure). So, by definition, the density of water is 1 gram per cubic centimeter, or 1 g/cc.

In the sample data, the mass of the water was 49 g and the volume was 50 cc. Thus, the density was 49 g/50 cc. This is close to one. The density of water is 1 g/1 cc but because of the limitation of the measuring equipment and impurities in the water, you should not be disappointed if your results are not exactly 1 g/1 cc. For example, in the sample data, 49 g ÷ 50 cc = 0.98/1 cc and round to the nearest tenth, 1.0 g/1 cc in the table.

Find Density as a Ratio. Sinking and floating depend not on mass or volume alone but on the ratio of mass to volume. This ratio is called density. Read together and discuss the Density section before Question 8. Students write the densities of the objects in their tables on the Sink and Float Data Tables page in the Student Activity Book for Question 8. To help them find a pattern, they organize their density information in a table of objects that sink and a separate table of objects that float as shown in Figure 4.

Find Patterns. After computing densities, students look for patterns in their tables to help them predict whether an object will sink or float in water (Question 9). These are some of the patterns they might notice:

If the mass of an object (in grams) is larger than its volume (in cubic centimeters), then it sinks; otherwise it floats.
If the density of an object is greater than 1 g/cc (the density of water), then it sinks; otherwise it floats.

Students apply their pattern in Question 10. They determine that the density of the object is M/V = 30 g/40 cc, which is less than 1 g/cc. Therefore, the object will float. To answer Question 11, they should reply that there isn't enough information to determine whether the object will sink or float. We need to know its volume as well as its mass.

In Question 12, students notice the M/V ratio for water is 1 or close to 1, while the ratios of the objects that sink or float are greater or less than one.

In Questions 13–14, students consider that an object sinks or floats in relation to the M/V ratio (density) of water 1 g/1 cc.

Use Ratios to Solve Problems. Discuss Question 15. Question 15A is an old riddle: Which is heavier, a pound of feathers or a pound of lead? This is a trick question, but if students aren't fooled, they will say, “neither, they both weigh the same amount—1 pound.” Question 15B is not a trick: Which is denser, a pound of feathers or a pound of lead? To compare the densities, we only have to look at the volumes, since the masses are the same. The volume of a pound of lead is much smaller than the volume of a pound of feathers, so the denominator in the density M/V is smaller for lead than feathers. Since the numerators are the same, the density of lead is greater than the density of feathers.

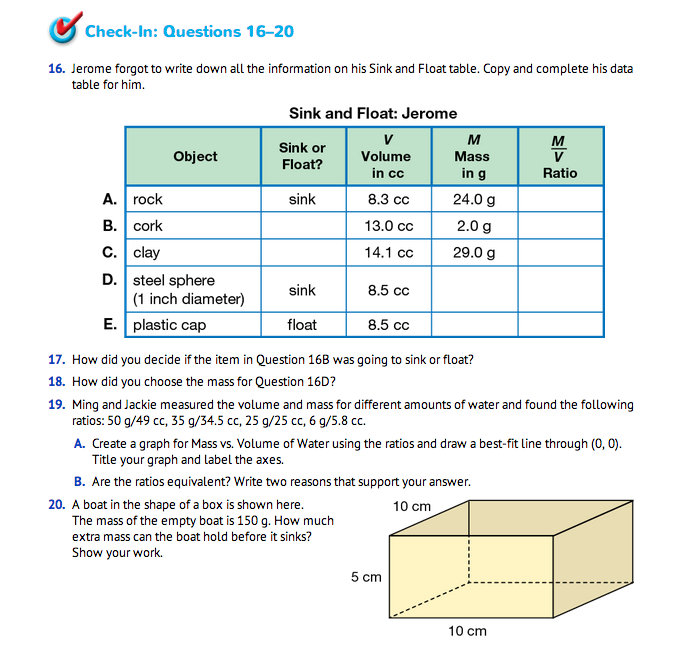
Assign Check-In: Questions 16–20 for students to complete independently. In Questions 16–18 students use what they have learned about the M/V ratios to complete Jerome's Sink and Float table. For Question 19, students use Centimeter Grid Paper to create a graph given the data collection ratios for Mass vs. Volume of Water and give reasons to support whether the ratios are equivalent or not. The collection data is close to one, so the ratios could be considered equivalent; however, because of the limitations of measuring equipment or water impurities, the ratios are not exact. Students could support either answer for equivalency depending on their reasons.

Use Check-In: Questions 16–20 in the Student Guide to assess students' abilities to represent the relationship between variables as a ratio [E2]; use ratios and proportions to solve problems [E4]; collect and organizing data into a table and line graph to represent the relationship between variables [E10]; make point graphs and drawing best-fit lines to represent ratios and proportional relationships [E11]; and use patterns in tables and line graphs to make predictions and solve problems [E12].

For Question 20, the mass of the empty boat is M = 150 g. Its volume is 10 cm × 10 cm × 5 cm = 500 cc. The density of the empty boat is 150 g/500 cc, so, of course, the empty boat will float. The numerator is less than the denominator (in other words, the ratio is less than 1 g/cc). Putting cargo in the boat will increase the mass (the numerator), but not the volume. As long as the extra mass is less than 350 g, the total mass will be less than 500 g. Then, the ratio M/V will be less than 500 g/500 cc = 1 g/cc, and the boat will float.