Lesson 5

Explore Circumference and Diameter

Est. Class Sessions: 4

Developing the Lesson

Part 1: Explore Circles

Introduce Circumference and Diameter. Read together the vignette of Nila and Jason talking about the Ferris wheel at Navy Pier in Chicago in the Explore Circumference and Diameter pages in the Student Guide. Display the circle diagram on this page for students as they read the definitions of the parts of the circle on the next page. This introduces students to the idea of measuring circles or circular-shaped objects and the corresponding terminology.

Ask students these or similar questions:

X
  • How could you show that every diameter has the same length? (Possible response: If I measured several times through the center point of the circle, the answer would be the same.)
  • How is the circumference of a circle like the perimeter of a rectangle? (Possible response: The circumference goes around the edge of the circle just like the perimeter goes around the edge of a rectangle.)
  • Nila knows how to measure the perimeter of a rectangle but not a circle. How do you think she measures the perimeter of a rectangle? (Possible responses: Measure the length of each of the four sides and add them together. Find the measurement for the length and the width and multiply by 2.)
  • What makes measuring the circumference of a circle different? (Possible answer: The curved edge can't be measured with a straight edge.)

If students have difficulty seeing that the circumference of a circle is a length, demonstrate the length with a trundle wheel or a piece of string.

X

Circles. In everyday language, a circle means a plane region bounded by a single curved line, every point of which is equally distant from the point at the center of the figure. It can also mean the boundary of such a figure. In mathematics, we use the latter meaning. It is a curve, not a region. The circumference of a circle can mean either the curve boundary of a circle (i.e., the circle itself) or the distance around the circle. A diameter of a circle is any line segment connecting two points on the circle and passing through the center. The diameter is the length of any diameter.

Discuss Ways to Measure Circumference. Have students discuss with a partner different ways that they could measure the circumference of a circle (Question 1A). Circulate and listen for student ideas such as laying string, yarn, ribbon, or wire around the circumference and then measuring its length, or using a sewing tape measure or other tape measure that bends. Select student pairs to share their ideas with the class. Have students discuss with a partner different ways that they could measure the diameter of a circle (Question 1B). Circulate and listen for student ideas such as using a ruler, measured string, and noting that the diameter measurement goes through the center point of the circle.

Students will use string in this activity to get a sense of the relationship between the circumference and the diameter of a circle. They will compare the length of string that measures the circumference to the length of the string that measures the diameter.

X

To develop an intuitive understanding of circles, choose a student to be the center. Choose 10 other students and tell them to stand 1 meter from the center. These 10 students will form (part of) a circle.

Encourage students to list the circles or circular-shaped objects that they see. Discuss the fact that the circular-shaped objects in the classroom are threedimensional, but that for this lesson students are examining two-dimensional circles. Make a list of the objects on the chalkboard. Some possibilities are:

  • a circular clock face
  • a circular rim of the trash can
  • a coffee can cylinder
  • circular lids to containers
  • a circular table
  • a circular opening of a pot for a plant
  • spools of thread
  • masking tape rolls
  • soup cans
  • wheels on a wheelchair or cart

Choose one of the objects and hold it so that the class can see it. Discuss the appropriate place to measure the circumference and the diameter of the object. If a can has grooves or dents, for example, these are not good places to measure the circumference.

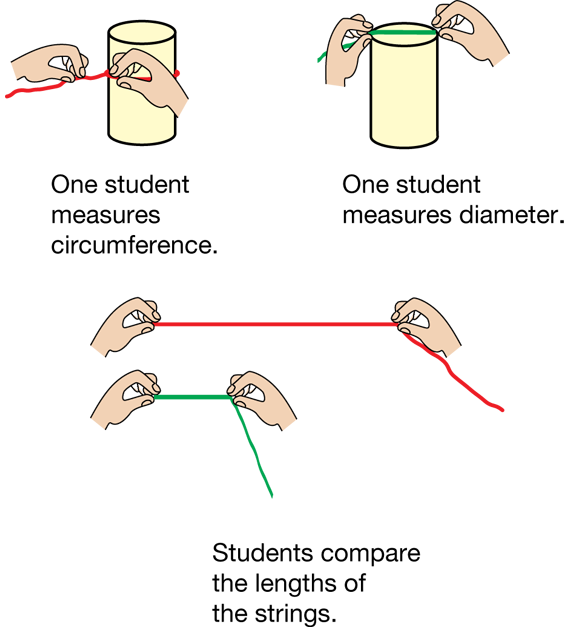
Measure Circular Objects. Assign pairs of students several circular objects to measure. Try to vary the size of the objects. Give each pair of students two lengths of string. Ask pairs to measure and explore the circumference and diameter of their circles with the string (Question 2).

X

Use string that does not stretch or it will make it more difficult for students to recognize the relationship between the circumference and the diameter.

One student should measure the diameter, while the other measures the circumference. If students have difficulty measuring the circumference, have one partner hold the end of the string on the object, while the other wraps it around. Measurements for the diameter should go through the widest part of the circle. Pairs should then hold up their lengths of string and compare them as shown in Figure 1 (Question 3).

Have students cut off the extra string to show the lengths. They can then lay these lengths down and compare them side by side. Students may need to fold the length of the circumference into thirds to verify that the circumference is indeed about three times the diameter.

X

Tack students' lengths for the circumference and the diameter for a variety of circles on a bulletin board. Label the strings appropriately as circumference or diameter. This will further reinforce students' understanding that the circumference of a circle is always about three times the diameter regardless of the size of the circle.

Discuss Relationship between Circumference and Diameter. After students have measured and made their estimates, discuss the relationship between the two lengths of string. With all the information from the class, students should see that the circumference is about three times longer than the diameter. The relationship between the circumference and the diameter does not change, no matter how large or small the circle. There are always about three diameters in the circumference.

Once student pairs have explored a variety of circles and have discovered the relationship, encourage them to answer Question 4. They can estimate that the circumference of the Ferris wheel is 3 × 150 feet or 450 feet.

Explain to students that the relationship they explored is only an approximation. Discuss with students whether the actual relationship is more or less than three.

Student Guide: 551 552
Answers
X
SG_Mini
+
X
SG_Mini
+
Student Activity Book:
Master:
Finding the relationship between the circumference and diameter of a circle
X
+