C
Cartesian Coordinates
A method of locating points on a flat surface by means of numbers. This method is named after its originator, René Descartes. (See also coordinates.)
pages 249–251
categorical variable
Variables with values that are not numbers, e.g., eye color, favorite food, ice cream flavors. (See also variable and value.)
pages 4, 16, 36, 40, 44, 46, 48, 51
centimeter
A unit of length in the metric system. A centimeter is 
of a meter.
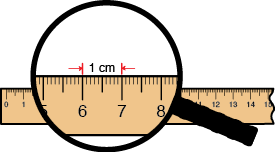
pages 186, 188, 189–194, 236–237, 271–273, 275, 360–361, 381, 415, 554, 555–558
circle
A two-dimensional (2-D) shape that is curved. Every point of the curve is the same distance from the center.
pages 58–63, 366, 551–559
circumference
The length of the distance around a circle or another round object.
pages 551–559
cluster
A group of data that are close together.
page 338
column
In an array, the objects lined up vertically.
pages 3, 166, 181–185, 217, 252, 353, 376, 382, 386, 422, 439, 441, 449, 507, 530, 555
column method
A division method.
pages 299–300, 304–305
combination method
A method of using more than one strategy for solving a problem, e.g., all-partials and compact.
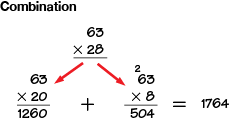
pages 183, 185
common denominator
A denominator that is shared by two or more fractions. A common denominator is a common multiple of the denominators of the fractions. 15 is a common denominator of 
and 
since 15 is divisible by both 3 and 5. = 
and = 
.
pages 94, 98, 105, 111, 389, 458–459, 460–465, 470, 472–473, 475, 477, 504, 515
common fraction
Any fraction that is written with a numerator and denominator that are whole numbers. For example, 
and 
are both common fractions.
(See also decimal fraction.)
pages 368, 381–382, 386
commutative property of multiplication
Also known as the Order Property of Multiplication. Changing the order of the factors does not change the product. For example, 3 × 5 = 5 × 3 = 15. Using variables, n × m = m × n. (See also turn-around facts and turn-around rule.)
page 137
compact method
A method of problem solving by calculating one column at a time, starting on the right, and making trades.
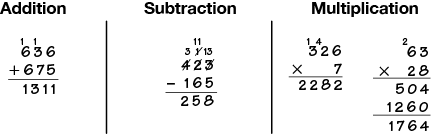
pages 181–185, 200, 307, 309
comparison division
Comparison division occurs when two set sizes are being compared. For example, how many times more apples are in Basket A as in Basket B?
compensation strategy
In compensation strategies, students adjust the numbers to make calculations easier. See the multiplication examples.
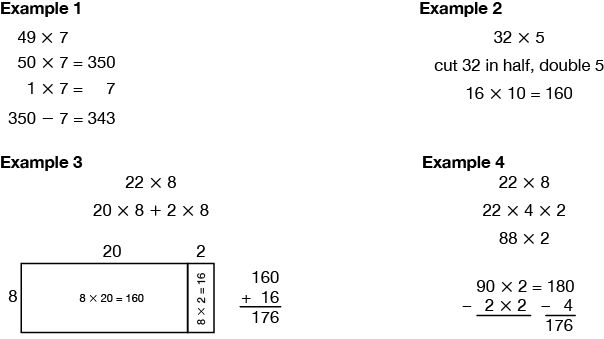
composite number
A number that has more than two distinct factors. For example, 9 has three factors (1, 3, 9) so it is a composite number. (See also prime number.)
pages 424–428, 431, 449, 454
congruent shapes
Congruent shapes have the same size and shape. Shapes are congruent if you can place one shape so it fits on top of the other and they match exactly.
pages 279, 285, 289, 290–292
consecutive
Following continuously.
page 429
convenient number
A number used in computation that is close enough to give a good estimate but is easy to compute mentally; e.g., 25 and 30 are convenient numbers for 27.
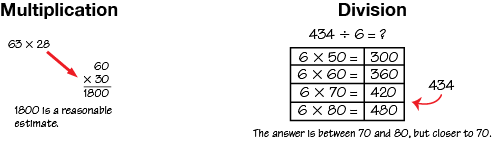
pages 136–143, 376, 418
convert
To change into a different form, system, or method.
pages 225, 229
coordinates
An ordered pair of numbers that indicate the position of a point on a flat surface by giving distances from a pair of coordinate axes. For example, if a point has coordinates (8, 3) it is 8 units from the vertical axis and 3 units from the horizontal axis.
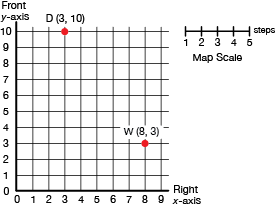
pages 249–270, 271–273, 274–275, 276–281, 531
cryptography
The study of secret codes.
page 430
cube
A three-dimensional shape with six congruent square faces.
pages 195–199
cubic centimeter (cc)
The volume of a cube that is one centimeter long on each edge.
pages 195–199, 205, 207–208, 340, 538–542, 543–550
cubic number
A number that is the result of multiplying a whole number by itself and by itself again. For example, 8 is a cubic number since 2 × 2 × 2 = 8.