B
bar graph
A graph that uses bars to show data.
pages 4, 6, 10, 11, 17, 42–43, 46
base (of an exponent)
When exponents are used, the number being multiplied is the base. In 34 = 3 × 3 × 3 × 3 = 81, 3 is the base and the 4 is the exponent.
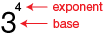
page 94
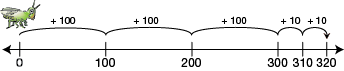
base-ten hoppers
A hopper that can make hops with distances of one, ten, one hundred, and one thousand on number lines. Base-ten hoppers can go forward or backward.
pages 116–122, 123, 227, 482
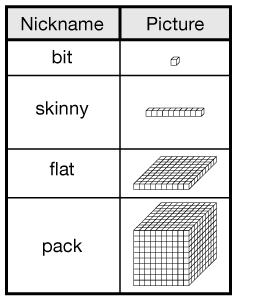
base-ten pieces
A set of blocks used to model our number system. Note that a skinny is made of 10 bits, a flat is made of 100 bits, and a pack is made of 1000 bits.
pages 108, 111–113, 115, 128–131, 133–134, 137–139, 143, 227–231, 264, 266, 284–285, 459–461, 467–472
base-ten recording sheet
A tool used to help organize base-ten pieces when they are used to represent numbers. In the example, the number 236 is represented.
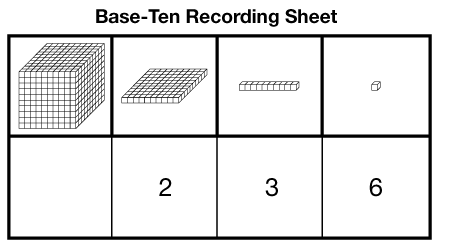
pages 108, 113, 128, 131, 135, 137
base-ten shorthand
A picture drawn to represent the base-ten pieces.
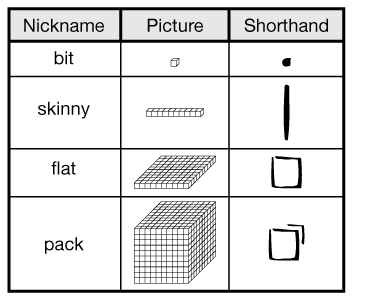
pages 112–115, 128–129, 135, 139, 227, 459–461, 469–470, 472–473
benchmark
Numbers convenient for comparing and ordering numbers;
e.g., 0, 
, and 1 are convenient benchmarks for comparing and ordering fractions.
pages 147–148, 232, 238–240, 317–319
best-fit line
The line that comes closest to the points on a point graph.
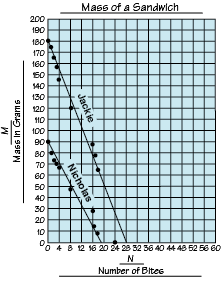
pages 29, 167, 188, 190, 195, 225, 248–249, 476, 563, 565, 574, 576
binning data
Placing data from a data set with a large number of values or large range into intervals in order to more easily see patterns in the data.
bit
The smallest of the base-ten pieces that is often used to represent 1. (See also base-ten pieces.)
pages 108, 112, 115, 228–230, 470
break-apart products
Breaking a number in a multiplication problem into smaller numbers to create easier numbers to multiply by, then adding the parts together to find the total of the original problem.
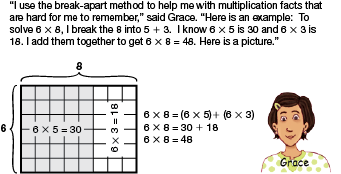
pages 86–87, 103–105