C
carry
A reminder of the amount to move forward to the next column if the answer is larger than the place value.

pages 287, 501, 505
categorical variable
Variables with values that are not numbers; e.g., eye color, favorite food, ice cream flavors. (See also variable and value.)
pages 8, 10, 38, 43, 46, 186, 478
centimeter
A unit of length in the metric system. A centimeter is 
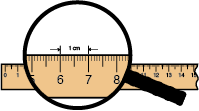
pages 19, 36–37, 61, 178, 180–181, 184, 422, 450, 452
circumference
The length of the distance around a circle or another round object.

pages 177–182
classify
To sort into formal categories. For example, angles can be sorted, or classified, based on their size.
pages 370, 422–424
column
In an array, the objects lined up vertically.
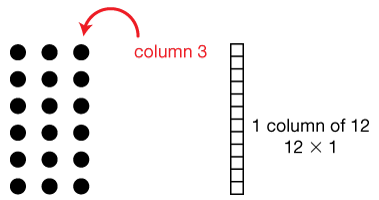
pages 30, 36, 39, 57–58, 69, 103, 159, 225, 258, 287–288, 502, 504–506, 562–564, 574–575
column method
A division method.
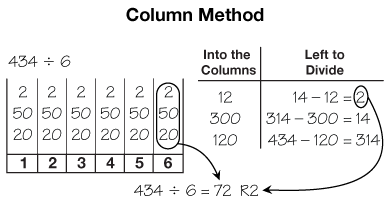
pages 536–537, 540, 544
combination method
A method of using more than one strategy for solving a problem; e.g., all-partials and compact.
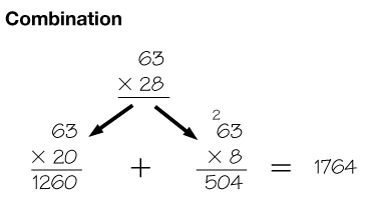
pages 502, 504, 506
common fraction
Any fraction that is written with a numerator and denominator that are whole numbers. For example, 

pages 454–456, 459–462, 463–464, 466–473
commutative property
Changing the order of the factors or addends does not change the product or sum.
| 3 × 5 = 5 × 3 = 15 |
| 4 + 5 = 5 + 4 |
| 2 × 3 × 4 = 3 × 4 × 2 |
| 10 × 8 = 8 × 10 |
page 265
compact method
A method of problem solving by calculating one column at a time, starting on the right, and making trades.

pages 138, 159–160, 281, 287–289, 501–507, 547–549
comparison division
Comparison division occurs when two set sizes are being compared. For example, how many times more apples are in Basket A as in Basket B?
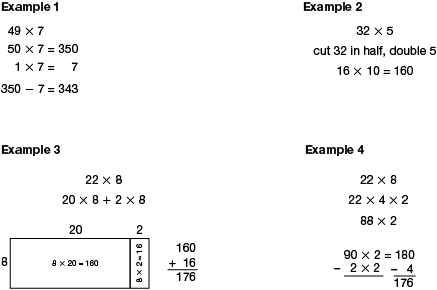
compensation strategy
In compensation strategies, students adjust the numbers to make calculations easier. See the multiplication examples below.
composite number
A number that has more than two distinct factors. For example, 9 has three factors (1, 3, 9) so it is a composite number.
concave
A shape is concave if any of the line segments connecting any two points in the interior of the shape are not completely in the interior of the shape.

congruent shapes
Congruent shapes have the same size and shape. Shapes are congruent if you can place one shape so it fits on top of the other and they match exactly.

pages 416–417
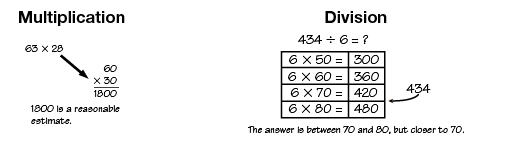
convenient numbers
A number used in computation that is close enough to give a good estimate but is easy to compute mentally; e.g., 25 and 30 are convenient numbers for 27.
pages 149, 238, 241, 271–274, 276–277
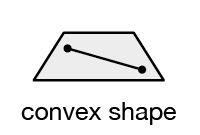
convex
A shape is convex if all the line segments connecting any two points in the interior of the shape are completely in the interior of the shape.
coordinates
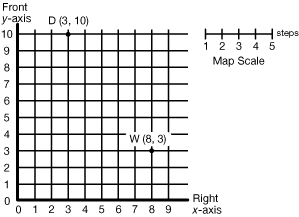
An ordered pair of numbers that indicate the position of a point on a flat surface by giving distances from a pair of coordinate axes. For example, if a point has coordinates (8, 3) it is 8 units from the vertical axis and 3 units from the horizontal axis.
core square
A square-shaped pattern used as the primary image in a quilt. The core square can be slid, turned, or flipped to create different designs.

pages 412–414, 418
counting back
A subtraction strategy in which students start from a larger number and then count down the smaller number until the difference is reached. For example, to solve 8 − 3, begin with 8 and count down three: 7, 6, 5.
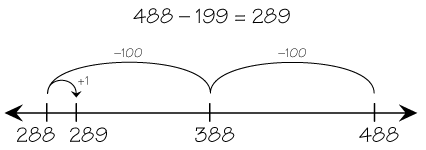
page 143
counting on
An addition strategy where the student starts with one number and counts forward the value of the second number to find the total.
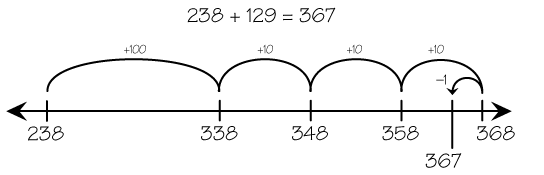
counting up
A subtraction strategy where the student starts at the lower number and counts on to the higher number. For example, to solve 8 − 5, the student starts at 5 and counts up three: 6, 7, 8. So 8 − 5 = 3.
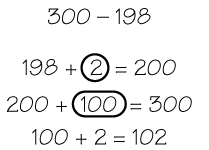
page 143
cubic centimeter(s) cc
The volume of a cube that is one centimeter long on each edge.
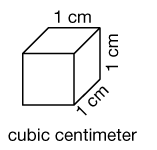
pages 554, 566–568
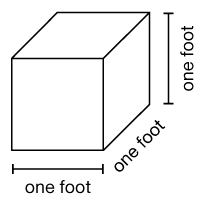
cubic foot
The volume of a cube that is one foot long on each edge.
cubic unit
A cube whose sides measure one unit.
page 554
cups
A unit of volume equal to 8 fluid ounces; one-half pint.
pages 294, 300, 310, 316, 334–336, 348, 355, 361, 535–537, 570










