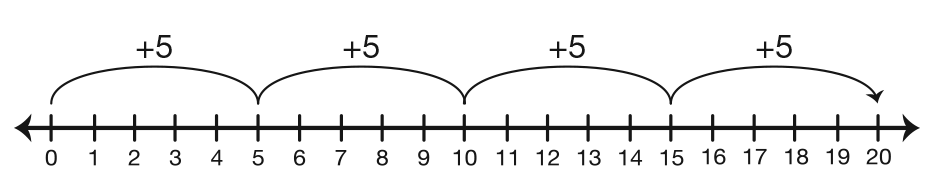Working with Groups

Est. Class Sessions: 2

Developing the Lesson

Part 1: Making Equal Groups

Repeated Addition. Introduce the lesson by distributing tiles to student pairs. Explain that students will work with equal rows of tiles. Ask students to make 6 rows of 2.

Begin by placing 2 tiles in a row and say:

This is one row of two. Continue until you have 6 rows of two.
How many tiles are there altogether? (12 tiles)
What is an addition sentence that describes these rows? (2 + 2 + 2 + 2 + 2 + 2 = 12 tiles)

Point to the tiles that each number relates to in the number sentence.

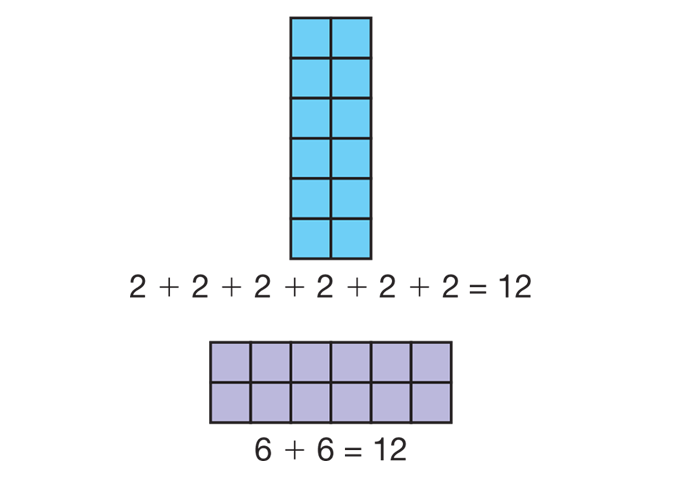
When you say 6 rows of 2, what do the numbers 6 and 2 represent? (The 6 is the number of rows and the 2 is how many tiles are in each row.)

Ask students to leave their 6 rows of 2 tiles on the side of their desks. Next ask students to make 2 rows of 6.

Ask:

How many tiles are there altogether? (12 tiles)
What is an addition sentence that describes these rows? (6 + 6 = 12 tiles)
Compare the 6 rows of 2 and the 2 rows of 6. How are they alike? (Possible response: They both have 12 tiles.)
How are they different? (Possible response: 6 rows of 2 is taller and 2 rows of 6 is wider.)

Demonstrate how to rotate the 6 rows of 2 tiles to show 2 rows of 6 tiles. See Figure 1.

Ask:

If I turn the 6 rows of 2, does it look like the 2 rows of 6? (yes)
Do 6 rows of 2 equal 2 rows of 6? How do you know? (yes; Possible response: When I count 6 rows of 2 tiles I get 12 and when I count 2 rows of 6 tiles I get 12.)
Is 2 + 2 + 2 + 2 + 2 + 2 = 6 + 6 a true statement? How do you know? (Yes, both sides of the equal sign show 12.)

Next ask students to make the following groups:

3 rows of 4 and 4 rows of 3
4 rows of 2 and 2 rows of 4
5 rows of 5

With each grouping, have students write repeated addition number sentences, show how the groupings relate to the number sentences, and compare the related groups of tiles (e.g., 3 rows of 4 and 4 rows of 3).

Ask:

For 5 rows of 5, is it possible to turn it so that I have a different number sentence? (No, it’s still 5 rows of 5 if you turn it.)

Have student pairs work to complete the How Many Tiles pages in the Student Activity Book using tiles as needed.

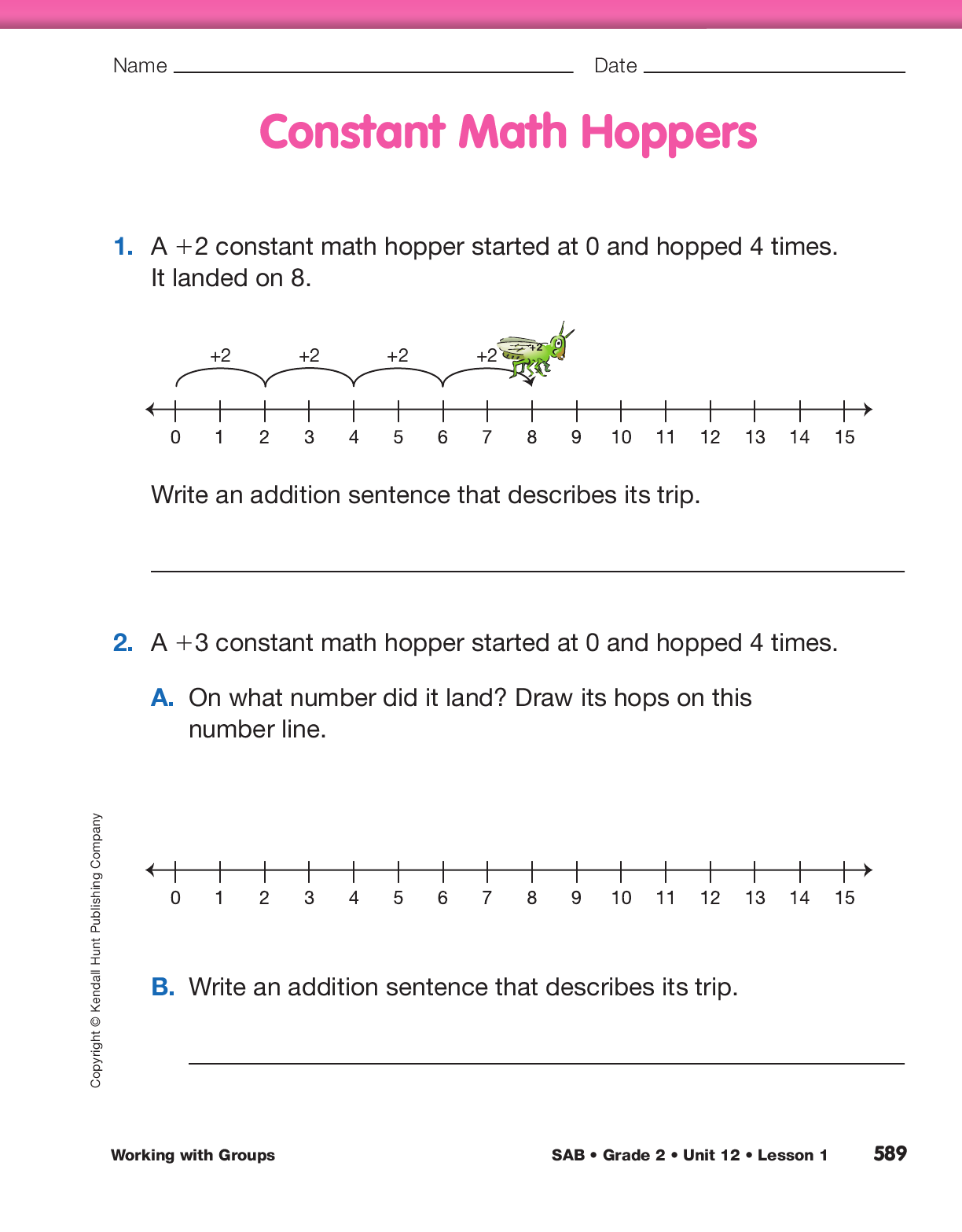
Constant Math Hoppers. Remind students that they have solved problems about math hoppers in previous units. Base-ten hoppers can hop in distances of one, ten, and hundred. Explain that students will investigate constant hoppers, which are math hoppers that always hop a constant amount. Explain that constant means unchanging. For a constant math hopper, the distance it jumps on each hop does not change.

Use the display of the Constant Math Hopper Number Lines Assessment Master to introduce constant hoppers. Choose a number and demonstrate how a hopper jumps if it can only make jumps of that length.

Present a problem such as the following:

Here is a +5 (“plus five”) hopper. It always hops 5 units to the right.
If it starts at 0 and hops 4 times, where will it land? (20)

Demonstrate on a number line. See Figure 2. Ask:

Tell an addition sentence that describes its trip.
(5 + 5 + 5 + 5 = 20)
Describe how each number in the number sentence connects to the constant math hopper’s trip. (The five is for how far it goes on each hop. It hopped four times. The 20 is where it stops.)
Why are there four 5s? (because it hopped four times)

Have students use tiles to show how the math hopper hopped.

Ask:

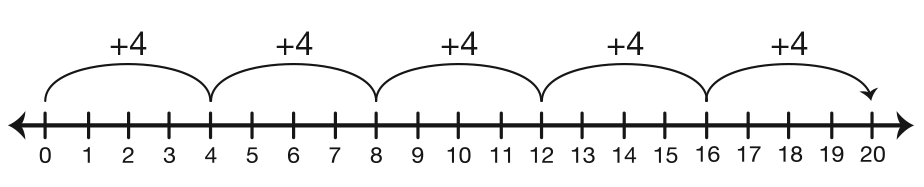
Explain how your tiles are arranged to show how the math hopper hopped on the number line. (Possible response: I made 5 rows of 4 and that equals 20.)

Next present a +4 hopper.

Say:

Here is a +4 (“plus four”) hopper. It always hops 4 units to the right.
If it starts at 0 and hops 5 times, where will it
land? (20)

Demonstrate on a number line. See Figure 3. Ask:

Tell an addition sentence that describes its trip.
(4 + 4 + 4 + 4 + 4 = 20)
Describe how each number in the number sentence connects to the constant math hopper’s trip. (The four is how far it goes on each hop. It hopped 5 hops. The 20 is where it stops.)
How are 4 hops of 5 and 5 hops of 4 alike? (Both land on 20.)
How do you know that 5 + 5 + 5 + 5 = 4 + 4 + 4 + 4
+ 4? (Both equal 20.)
How could you use math tiles to show
5 + 5 + 5 + 5 = 4 + 4 + 4 + 4 + 4? (I could make 4 rows of 5 tiles and turn it to make 5 rows of 4 tiles. They both have 20 tiles.)

Make up a few more problems about constant math hoppers that start at 0 and hop to the right. Ask students to demonstrate how the hopper moves on a number line. The number of hops and the size of each hop determine where the math hopper stops. Have students write repeated addition number sentences and explain how each number in the number sentences connects to the constant math hopper’s trip. Each time, turn the numbers around and demonstrate how the number sentences result in the same answer.

You can introduce constant math hoppers by making a large number line on the classroom floor, playground, or sidewalk with chalk. Students can pretend to be the constant math hoppers and act out the math problems.

Students can use a green pattern block as a hopper on their desk number lines, pointing a corner of the triangle where it lands.

Once students are familiar with constant math hoppers, have them work in pairs to complete the Constant Math Hoppers pages in the Student Activity Book using their desk number lines or tiles as needed. For each problem, students determine where the math hopper lands, the number of hops, or the size of each hop.

Point out to students that the arrows on the hops should point to the right since the constant hopper is moving from zero to larger numbers. Remind them to label the hops with the number of units (e.g., +5, as in Figure 2 or +4 as in Figure 3).

As students finish, ask them to explain how they found their answers for Question 5 and Question 6. These questions may have presented a challenge for some students since they were not told what kind of a constant math hopper was involved. They had to solve the problem in some way other than making hops on their number lines. Ask students to check their answers by showing the hops on their number lines.

ADVENTURE BOOK: