Grouping and Sharing
The concepts of multiplication and division are important content for Second-Grade students. There is strong evidence that these students are … read more
The concepts of multiplication and division are important content for Second-Grade students. There is strong evidence that these students are able to solve multiplication and division problems when the problems relate to familiar situations and when the emphasis is on representing problems with manipulatives and pictures.
This unit incorporates the following key features concerning multiplication and division:
- Children’s knowledge of multiplication and division emerges from engaging and interesting problems.
- Everyday situations and language for the operations are emphasized.
- Thinking strategies for solving problems are encouraged.
- Computational skills, such as memorization of facts and calculation with multidigit numbers, are not a focus.
Both multiplication and division are presented in this unit since these operations are closely related. The thinking processes children use to solve multiplication and division problems are often closely related as well.
In this unit, students approach multiplication primarily as repeated addition. For example, if 3 monkeys are each fed 4 bananas, how many bananas are eaten in all? Number sentences for this problem are 4 + 4 + 4 = 12 and 3 x 4 = 12. In Third and Fourth Grades, we will introduce other ways for students to think of multiplication.
The division problems that students solve fall into two basic categories. Usually these are called partitive division (division by sharing) and measurement division. It is not important for students to distinguish between the two types of division situations, but rather to have experience with both.
Partitive Division
Partitive division (division by sharing) includes … read more
Partitive Division
Partitive division (division by sharing) includes problems such as: There are 8 bananas to be shared by 4 monkeys. How many bananas will each monkey get? In other words, if 8 bananas are divided into 4 groups (or partitions), how many bananas are in each group? The number of groups is known but the number of objects in each group is not.
Measurement Division
Measurement division includes problems … read more
Measurement Division
Measurement division includes problems such as: There are 12 bananas. Each monkey needs 2 bananas. How many monkeys can be fed? In other words, if 12 bananas are divided (measured out) into groups of 2 bananas each, how many groups are there? The measure, or size, of each group is known but the number of groups is not. In both situations, students know how many in all and want to find out about equal groups.
Students solve the multiplication and division problems
by considering the real situations and using
strategies, tools, and cubes or other manipulatives to
model them. They are able to solve the problems
not because they have been shown an algorithm or
procedure, but because they can understand the context.
It makes sense to them. See Figure 1.
Similarly, students use their understanding of real
situations to address the issue of what to do with
leftovers in a division problem. They make their
decisions based on their understanding of the contexts.
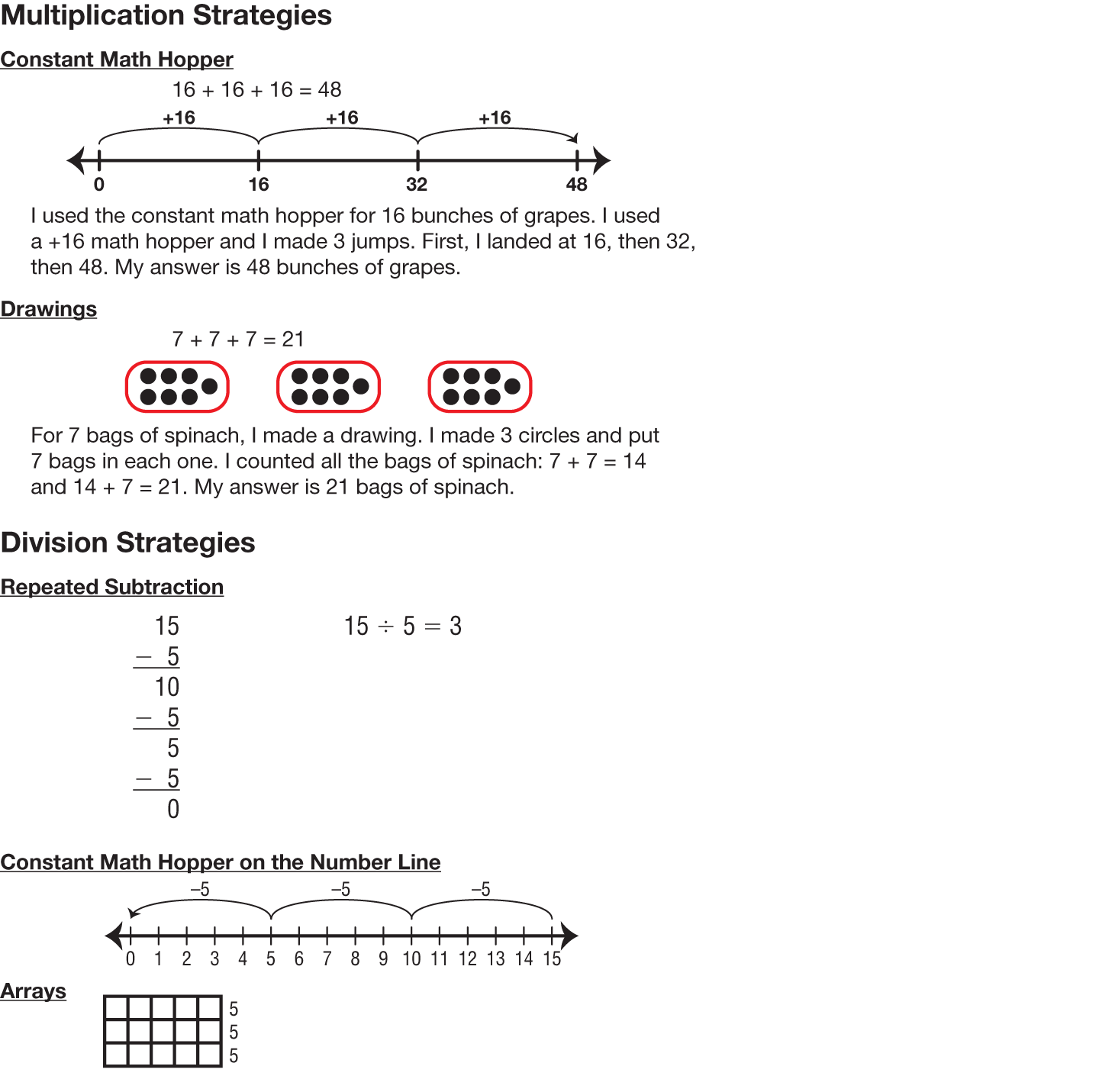
Figure 1: Sample strategies for solving multiplication and division problems
NOTES on PROBLEM SOLVING APPROACHES

As students write and solve problems, the primary emphasis should be on encouraging them to think of various ways to solve problems and on having them … read more
As students write and solve problems, the primary emphasis should be on encouraging them to think of various ways to solve problems and on having them share their problem solving strategies with their classmates. Encouraging students to invent and use a variety of strategies and representations allows students to access the problem in ways that make sense to them. Students build deeper conceptual understanding by connecting their strategy to their classmates’ strategy. One useful way to categorize problem solving approaches is to group them into three types: concrete, visual, and symbolic. To illustrate each of these approaches, we will use the following problem: Three monkeys were each fed 17 peanuts. How many peanuts were eaten altogether?
Students who rely on a concrete approach use peanuts (or connecting cubes that represent peanuts). Among these students, there are a variety of strategies for finding the total number of peanuts. For instance, some students may first count the tens and then group the peanuts into three groups of seven and count them by ones or regroup them in order to count them by fives or tens.
Students using a visual approach may draw pictures to represent the problem situation. Students are encouraged to draw pictures to solve problems for the following reasons: (1) a drawing provides them with a permanent record of their thinking, (2) paper and pencil is a readily available tool (while manipulatives may not be), and (3) overemphasis on symbolic and rote procedures can inhibit their understanding.
Resources
- Burns, M. “Introducing Division through Problem-Solving Experiences.” In The Arithmetic Teacher: Mathematics Education through the Middle Grades. National Council of Teachers of Mathematics, Reston, VA, 1991.
- Carpenter, T.P., E. Ansell, M.L. Franke, E. Fennema, and L. Weisbeck. “Models of Problem Solving: A Study of Kindergarten Children’s Problem-Solving Processes.” In Journal for Research in Mathematics Education, 24 (5), pp. 427–440, 1993.
- Carpenter, T.P., D. Carey, and V.L. Kouba. “A Problem-Solving Approach to the Operations.” In
Mathematics for the Young Child,
pp. 111–131, J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990. - Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children’s Mathematics: Cognitively Guided Instruction. Heinemann, Westport, CT, 1999.
- Fosnot, C.T., and Dolk, M. Mathematicians at Work: Constructing Multiplication and Division. Heinemann, Portmouth, NH, 2001.
- Post, T.R. Teaching Mathematics in Grades K through 8: Research-Based Methods. Allyn and Bacon, Needham Heights, MA, 1992.
- Van de Walle, J.A. Elementary and Middle School Mathematics: Teaching Developmentally, 6th Ed. Pearson, Boston, New York, San Francisco, 2007.












