Introduce Arrays.
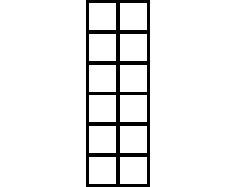
Display six rows of two tiles as
shown in Figure 1. Explain that the tiles are arranged
in an array, an arrangement of objects in rows and
columns. As you point to the rows and columns,
explain that a row runs horizontally, or across, and a
column runs vertically, or up and down.
-
Have you ever seen anything arranged in arrays? (Possible responses: stamps, stickers, desks, eggs, seats in an auditorium)
- How many tiles are in each row? (2)
- How many tiles are in each column? (6)
- What are some ways you can find how many total
tiles there are? (Possible responses: counting
each tile, skip counting by twos, doubling six,
adding
2 + 2 + 2 + 2 + 2 + 2 = 12 or 6 + 6 = 12)
Students may suggest counting the tiles by ones.
Encourage them to find more efficient ways of finding
the total. Having students think of number sentences
also encourages skip counting and repeated
addition rather than counting by ones.
- Is there a faster way to find the total without counting each tile? (Possible response: skip counting, repeated addition)
- What is a number sentence for this arrangement of tiles? (2 + 2 + 2 + 2 + 2 + 2 = 12, 6 + 6 = 12,
6 × 2 = 12, 2 × 6 = 12)
- What do the numbers in each multiplication number sentence represent? (The 2 stands for the
number of tiles in each row, the 6 stands for the number of rows, and the 12 represents the total number of tiles.)
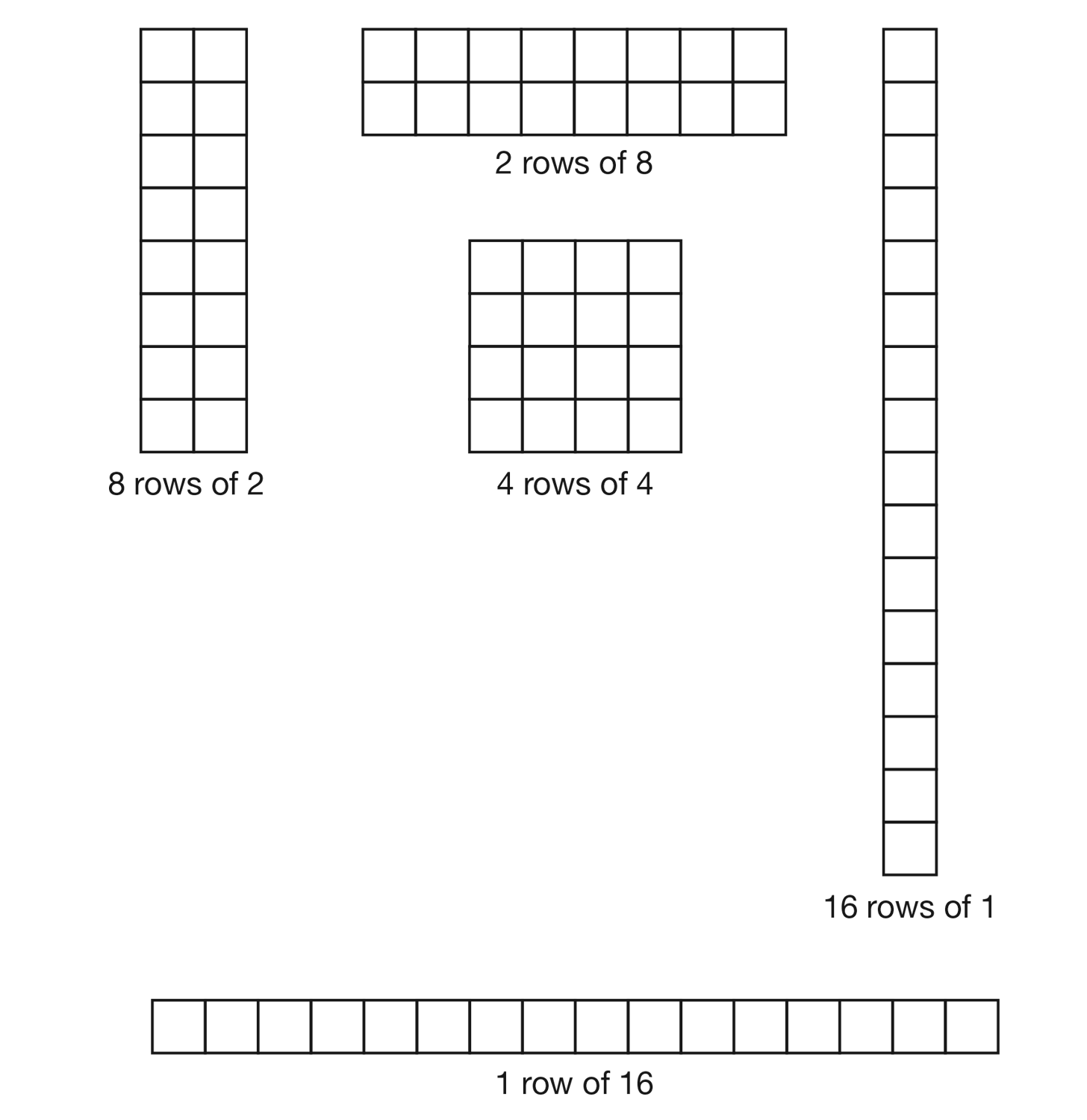
Tell student pairs to take 16 tiles and arrange them in rectangular arrays with each row having the same number of tiles. See Figure 2 for sample arrays.
- How did you arrange your 16 tiles? (Possible responses: 2 rows of 8, 8 rows of 2, 4 rows of 4, 1 row of 16, 16 rows of 1)
- How did you find the total number of tiles? (Possible response: I skip counted by 2s: 2, 4, 6, 8, 10, 12, 14, 16.)
- If you look at the tiles by row, what is a number
sentence for this array? (Possible response:
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 16)
- If you look at the tiles by column, what is a number
sentence for this array? (Possible number sentence:
8 + 8 = 16)
- Is 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 8 + 8? (yes)
- What is a multiplication number sentence for this arrangement? (2 × 8 = 16 or 8 × 2 = 16)
- What do the numbers in each multiplication number sentence represent? (The 2 represents how
many tiles in each row, the 8 stands for the number of rows, and the 16 represents the total number of tiles.)
- Is 2 × 8 = 8 × 2? How do you know? (yes; Possible response: If I look at the array, I can
describe it by row or by column: 2 rows of 8 or 8 columns of 2. They both equal 16.)
Repeat this activity a few more times using 10, 18, and 20 tiles.
Solve Array Problems. After discussing a few
arrays, have students complete the Zoo Stickers
pages in the Student Activity Book. Ask students to
write an addition and multiplication number sentence
to describe each set of stickers. Use a display
of the Zoo Stickers pages to record and discuss
students’ solutions and number sentences.
- Look at Michael’s stickers by row. What is an addition number sentence for his array?
(6 + 6 + 6 + 6 = 24)
- If you look at his stickers by column, what is an addition number sentence?
(4 + 4 + 4 + 4 + 4 + 4 = 24)
- What are two multiplication number sentences for
Michael’s stickers? (4 × 6 = 24 and 6 × 4 = 24)
- What do the numbers in the multiplication sentence mean? (4 rows, 6 columns, 24 total stickers)
- Is 4 × 6 = 6 × 4 a true number sentence? How do you know? (yes; Possible response: You have the
same number of stickers if you have 4 rows of 6 stickers or 6 rows of 4 stickers.)
- Is 6 + 6 + 6 + 6 = 4 × 6 a true sentence? How do you know? (Yes, because 6 + 6 + 6 + 6 is the same as
4 sixes.)
Repeat the discussion with Jacob’s and Linda’s stickers. Continue to ask students to identify what the numbers mean by
referring to the arrays of stickers.