Mr. Moreno overheard their conversation. He said to the class, “Felicia and Roberto have a good question. How accurate can the measurements of an irregular shape be? How close is close enough?”
He gave each student a copy of an irregular shape that was traced on Centimeter Grid Paper. He asked each student to find the area of the shape in square centimeters. Felicia, Roberto, and the three other students in their group estimated the area of Shape A. Felicia's and Roberto's work is shown below.
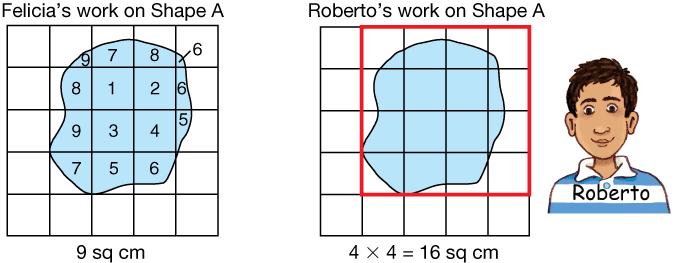
Roberto said, “I think Felicia's estimate is a closer estimate than mine. I counted every partial square as if it was a full square, even if it only had a little bit of the shape in it.”
Mr. Moreno said, “I agree that Felicia's estimate is closer to the actual area because of how she counted. But I can think of one way that your estimate could be helpful to us, Roberto. Do you think someone could make a larger estimate for the area of Shape A than you did?”
“Well, they could, but it sure wouldn't make much sense. There are only 16 squares that have any of the shape in them.”
Mr. Moreno answered, “That's right, Roberto. I'd say your estimate is the upper limit for a possible estimate. Could we say there is a lower limit for a possible estimate?”
“I think 4 square centimeters,” said Felicia, “because that is the number of totally full squares. So an estimate of 3 square centimeters wouldn't make any sense. Neither would an estimate of 17 square centimeters.”
“I agree with you, Felicia. Four and 16 square centimeters are our outer limits. But neither of these estimates are very close to the actual area, are they? Neither one takes into account the partial squares. How can we decide which estimates are close enough to the actual area to be useful to us? Which ones can we call good estimates?”












