Display the blue rhombus, trapezoid, triangle, and hexagon
pattern blocks.
- Which shape is a hexagon? How can you tell?
(It has six sides and six corners.)
Use a display of The First Grade Times page in the
Student Activity Book to introduce using other pattern blocks
to create hexagons. Tell students they can use a strategy called
trial and error to work on this problem. Some combinations will
work; others will not. Come to an agreement that one hexagon is
not a solution.
Divide the students into pairs to explore possible combinations.
Students can record their solutions on the First Grade
Times page, using crayons or markers. Demonstrate how to fill
in one solution. Point out that the dotted lines are guides and
they do not mean that triangles are always used. As students
work, they should outline and color the shapes they use with the
color of blocks they represent.
Each student pair should have a generous supply of pattern
blocks since some will want to find many ways before recording
their work.
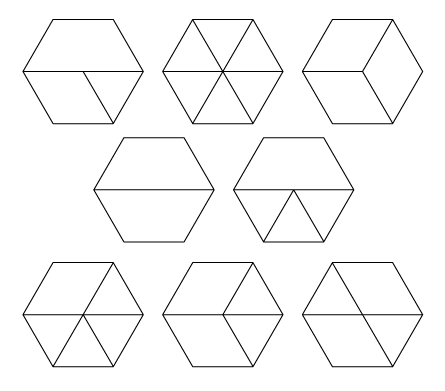
Encourage students to find as many different arrangements
as they can. Facilitate discussions about whether arrangements
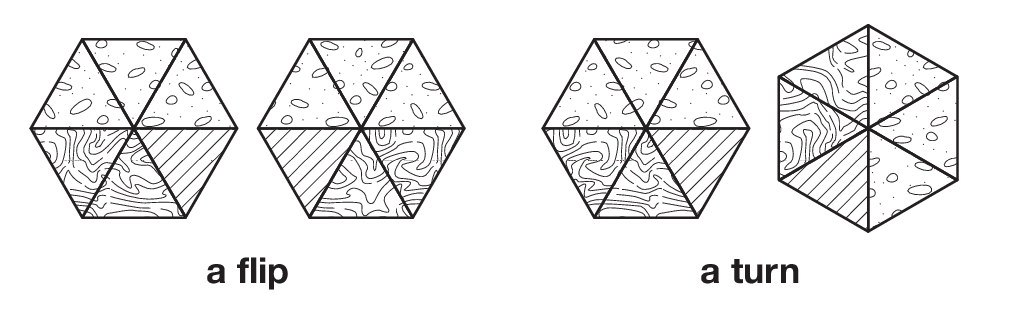
should be counted as alike or different. If they consider
arrangements that differ by a flip or a turn to be the same (see
Figure 1), then there are eight possible arrangements as shown in
Figure 2.
As they work together in pairs, ask questions that
encourage students to identify and name the shapes, focus on the
properties of the shapes, or probe their understanding of alike
and different.
- What shape did you just make? (hexagon)
- Describe how you made it. What shapes did you
use to make the hexagon? (Possible response: triangles and
rhombuses)
- How many of each shape did you use? (Possible
response: two triangles and two rhombuses)
- What shapes can you put together to make a
rhombus? (2 triangles)
- What shapes can you put together to make a
trapezoid? (3 triangles or a triangle and a rhombus)
- Can you find a side on the rhombus that matches
a side of a triangle? (yes)
- How can knowing what shapes you can put
together to make a rhombus and trapezoid help you find ways
to make a hexagon? (Possible response: It gives more ways
that I didn't think of, like when I used the rhombus I could
use two triangles instead.)
Tell students you will not answer an individual's question
unless he or she first discusses the question with his or her
partner. If both partners agree that they cannot answer the
question, then both students should raise their hands.
If you see a student pair that has two solutions
that are alike, ask:
- Look at these two solutions. Are they alike or
different? (Answers will vary.)
Some students may not understand that two hexagons both
showing six triangles are the same. Others will not be able to
discriminate between solutions that are merely rotations of one
another.
- What shapes did you use to make the two
hexagons? Did you use the same number of each shape in both?
- If you turn (rotate) this solution, does it
look the same as the other?
To help students communicate their thinking and
justify their solutions, ask:
- How is this arrangement different from this
one? (Possible response: They use different shapes. This one
uses all triangles and this one uses triangles and rhombuses.)
Observe students as they work to find partitions of the
hexagon on the First Grade Times page with the Feedback Box to
assess students' abilities to identify and name two-dimensional
shapes [E1]; compose and decompose two-dimensional shapes [E4];
justify their reasoning [E5]; and communicate their solutions
with words and pictures [MPE5]. Give students time to complete a
few solutions, then circulate through the classroom and have
students explain their thinking by asking questions such as:
- What shapes did you use to make this hexagon?
- How many of each shape did you use?
- How did you know which shapes to use?
- Are there pattern blocks you could put together
to make other shapes?
- Were there any pattern block shapes that did not
work? Why?