Mathematics in this Unit Print

Exploring Shapes

"Given children's affinity toward, knowledge of, and ability to gain geometric knowledge, it is important that this domain of mathematics not be neglected. Instruction in geometry needs to complement the study of number and operation in grades pre-K to 8" (National Research Council, 2001). Math Trailblazers echoes this expectation by emphasizing the importance of geometry in the mathematics curriculum.

This unit capitalizes on students' awareness of shapes from everyday experiences. Its approach to geometry involves identifying, describing, analyzing, comparing, contrasting, classifying, and copying shapes. They investigate the results of combining shapes (composing) and breaking them into smaller parts (decomposing). There are also activities that develop spatial and visual relationships.

This unit emphasizes the following:

  • linking shapes to the student's world and environment;

  • using both informal and conventional language to describe shape properties;

  • recognizing relationships among shapes;

  • visualizing shapes.

Students' work with pattern blocks will help develop their abilities to recognize relationships and visualize shapes. For instance, students learn that the trapezoid can be formed with one rhombus and one triangle or with three triangles as shown in Figure 1. They can use this observation in making substitutions when filling in a shape outline. Students use their spatial sense to find multiple ways to fill in the same space, as in Figure 2.


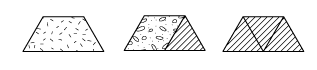Figure 1: Making a trapezoid with pattern blocks

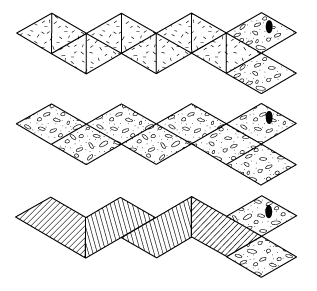Figure 2: Three of the many ways to fill in the outline of a snake

As students combine, construct, and visualize shapes, they will acquire a deeper understanding of geometric shapes and their properties. This, in turn, helps students develop their sense of relationships in space.

van HIELE LEVELS of GEOMETRIC DEVELOPMENT

Much of the approach to geometry found in the Math Trailblazers curriculum … read more

X

Much of the approach to geometry found in the Math Trailblazers curriculum is grounded in the insights of Dutch educators Pierre van Hiele and Dina van Hiele-Geldof. Ongoing research in mathematics education continues to confirm the five levels of geometric development first described by the van Hieles in the 1950s (Burger and Shaughnessy, 1986). The five levels are:

  • Level 0: Visualization. Students judge geometric objects by their appearance but not by attributes. For example, a square that is rotated becomes a diamond or kite and is no longer considered a square by a student operating at this level of thinking.

  • Level 1: Analysis. Students begin to describe the properties of objects. A figure is no longer judged because it "looks like one," but rather because it has certain properties. For example, all rectangles have the same properties. Each rectangle has four sides and four square corners or angles. Students begin to generalize about classes of shapes. For example, all four sides of a square are equal in length. Students can list properties of classes of shapes, but at this level they do not yet see class inclusion. That is, these students are unable to recognize that a square is a rectangle.

  • Level 2: Informal Deduction. Students logically order the properties of figures and are able to deduce that one property precedes or follows from another property. They see relationships among figures. For example, a square has all the properties of a rectangle; therefore, a square is a rectangle. Students may also be able to define a square based on its properties.

  • Level 3: Deduction. Students write formal proofs based in an axiomatic system. A rigorous high school geometry course is taught at Level 3.

  • Level 4: Rigor. Students can work with different axiomatic systems. This level corresponds to college work in geometry (Crowley, 1987; van Hiele, 1999).

The van Hieles found that each level, while not age specific, builds on the previous level. Students proceed from level to level sequentially and no level can be omitted. Advancement depends on content and method of instruction (Crowley, 1987; van Hiele, 1999). Moreover, a student's experiences with lower-level reasoning at the elementary school level are critical to success with geometry in later schooling. Students who are at Level 0 or 1 when entering high school geometry have a poor chance of success. Students who begin high school geometry at Level 2 have at least a 50% chance at succeeding (Senk, 1989). Unfortunately, many upper elementary students are still at Level 0. This is not surprising, as researchers have found that most geometry questions asked in standard elementary math textbooks were answerable with Level 0 understanding (Fuys, Geddes, and Tischler, 1988).

Five Phases of Geometric Thought

According to the van Hieles, the five phases leading to higher levels of geometric … read more

X

Five Phases of Geometric Thought

According to the van Hieles, the five phases leading to higher levels of geometric thought are as follows:

  • Information. Students get acquainted with examples and non-examples.
  • Guided orientation. Students participate in activities.
  • Explication. Students express relations in words.
  • Free orientation. Students learn by doing complex tasks.
  • Integration. Students summarize what they have learned.

Importance of Language

It is important to have students develop level-appropriate language around … read more

X

Importance of Language

It is important to have students develop level-appropriate language around the geometry they are exploring. At the same time, it is important for teachers to identify and use the appropriate language for the students' level of thinking or the student may not understand the teacher's explanations, questions, or comments.

As students describe their shapes, the teacher can help refine ideas they already have and introduce useful vocabulary as appropriate. For example, students may use the word "corner" when the teacher uses the word "angle." It is important to connect the two words so that students understand the ideas the teacher is addressing.

Solidifying Students' Geometric Thinking

It is important to have students develop level-appropriate language around … read more

X

Solidifying Students' Geometric Thinking

Students' geometric experiences add to their geometric thinking. Some students in Grades K–2, with appropriate experiences, can reach Level 1 of the van Hiele model. It is a goal of K–2 education that teachers offer geometric activities to help solidify students' Level 0 thinking and prepare them for thinking at Level 1. Some of these activities are described in the table in Figure 3. Many of these activities span both primary levels (Level 0 and Level 1). The level of the activity depends on how questions are asked and which shapes are involved. For example, in Unit 2 Lesson 5, students identify the familiar shapes that make up a "mystery shape." An activity that would address higher levels of geometric thought might be a more complicated mystery shape, or one that asks students to create a particular figure given a specific number of shapes. In general, the goals for geometry at the primary level are to refine and focus students' understanding of shapes, gradually develop a mathematical vocabulary, recognize and name parts or properties of two- and three-dimensional shapes, and focus on the attributes of various classes of shapes.


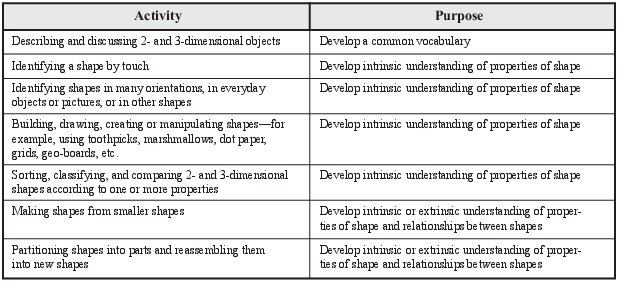Figure 3: Geometric experiences

Geometry offers students an aspect of mathematical thinking that is different from, but connected to, the world of numbers. As students become familiar with shape, structure, location, and transformations and as they develop spatial reasoning, they lay the foundation for understanding not only their spatial world but also other topics in mathematics and in art, science, and social studies. Some students' capabilities with geometric and spatial concepts exceed their numerical skills. Building on these strengths fosters enthusiasm for mathematics and provides a context in which to develop number and other mathematical concepts (Razel and Eylon, 1991).

From the National Council of Teachers of Mathematics Principles and Standards for School Mathematics, 2000.

Resources … read more
X

Resources

  • Burger, W.F., and J.M. Shaughnessy. “Characterizing the van Hiele Levels of Development in Geometry.” Journal for Research in Mathematics Education 17 (1), pp. 31–48, 1986.
  • Clements, D.H., and J.A. Sarama. Learning and Teaching Early Math: The Learning Trajectories Approach. Routledge, New York, 2009.
  • Crowley, M.L. “The van Hiele Model of the Development of Geometric Thought.” In Learning and Teaching Geometry, K–12. 1987 Yearbook, 1–16. Mary Montgomery Lindquist, ed. National Council of Teachers of Mathematics, Reston, VA, 1987.
  • Fuys, D., D. Geddes, and R. Tischler. “The van Hiele Model of Thinking in Geometry among Adolescents.” Journal for Research in Mathematics Education, Monograph Number 3, 1988.
  • National Research Council. “Developing Mathematical Proficiency beyond Number.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
  • Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
  • Senk, S.L. “van Hiele Levels and Achievement in Writing Geometry Proofs.” Journal for Research in Mathematics Education, 20 (3), pp. 309–321, 1989.
  • Van De Walle, J.A., K.S. Karp, and J.M. Bay-Williams, “Developing Early Number Concepts and Number Sense.” Elementary and Middle School Mathematics: Teaching Developmentally Eighth Edition. Pearson Education, Inc. Upper Saddle River, NJ, 2013.
  • van Hiele, Pierre M. “Developing Geometric Thinking through Activities That Begin with Play.“ In Teaching Children Mathematics, 5 (6), pp. 310–316, 1999.
  • Wilson, P.R., and A. Osborne. “Foundational Ideas in Teaching about Measure. ” Teaching Mathematics in Grades K–8, Research-Based Methods. T.R. Post, ed. Allyn and Bacon, Inc., Boston, 1988.