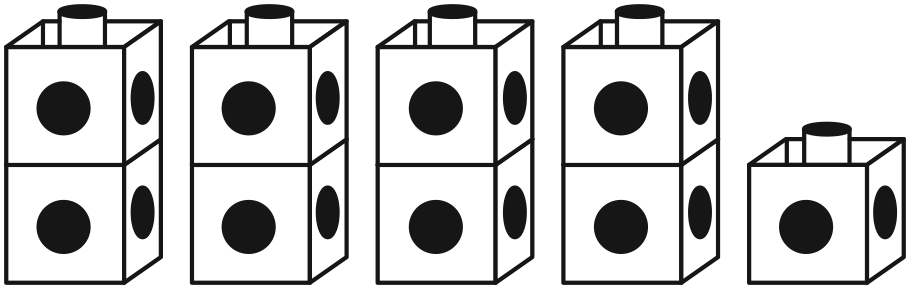
Make Pairs of Cubes. Ask students to use both
hands to scoop connecting cubes from a large container. Then ask students to stack the cubes in as
many pairs as possible and count their cubes. See
Figure 2. Tell them to count how many cubes they
have.
- Who was able to make pairs with all of their cubes?
- Who had leftovers after they made pairs with all of their cubes?
- Show your neighbor how you count your cubes. What strategy did you use? (Possible responses: I skip counted by 2 and then added the leftover; I did not have any leftovers, I just counted by 2.)
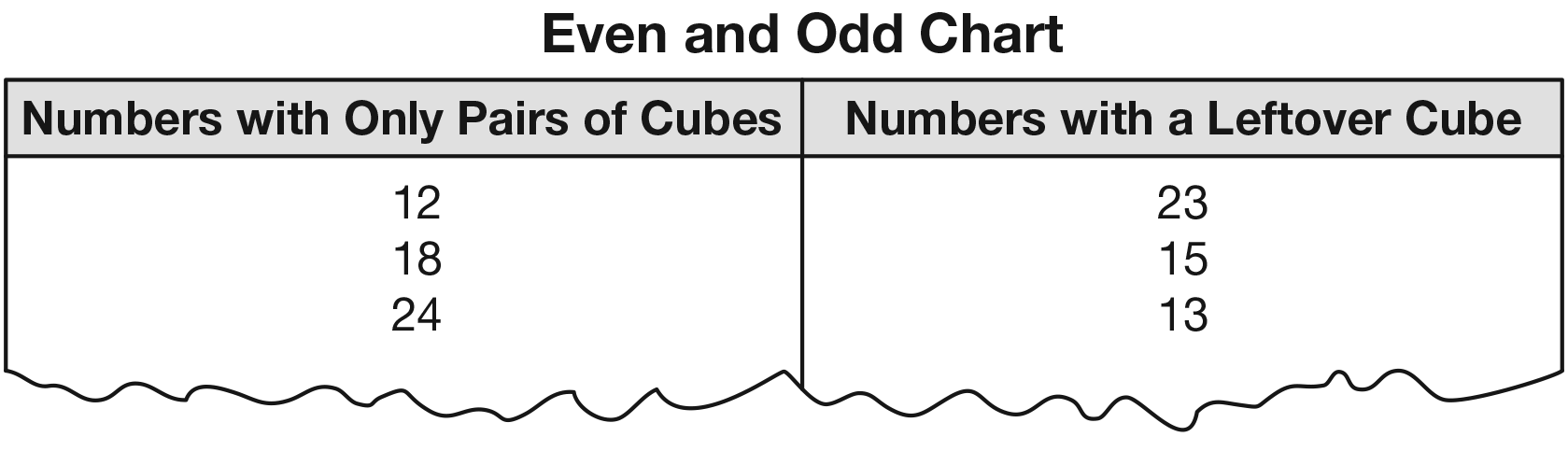
Refer students to the Even and Odd Chart you have
prepared and displayed.
Ask each student the following:
- How many cubes do you have in all?
- Where should I place your number? Did you have pairs for all your cubes? Or did you have a leftover cube?
Record each student's number in the appropriate column.
As students report their counts, occasionally ask:
- Do you agree with [student name]'s column choice?
- Why or why not?
The numbers in the table will likely be greater than
ten. Tell students to choose a number of cubes that is
ten or less and make pairs with cubes as before. Ask
students to tell you where to place each number on
the chart and why. Then record the numbers on the
chart.
Discuss Even and Odd Patterns. Tell students that
mathematicians have special names for the numbers
in each column of the data table. The numbers in one
column are called odd numbers and the numbers in
the other column are called even numbers.
- Which column do you think has the even numbers
and which column do you think has the odd numbers?
Ask students to discuss this question with a partner
and then discuss it as a class. See the Sample Dialog
for a sample class discussion.
Use the following
questions to guide the discussion:
- Think about how we use the words "even" and
"odd" in everyday language. How might this help
us decide?
- Why do you think [four] is an even number?
- Show us what you mean by pairs.
- What do you think makes a number odd?
- Why do you think [11] is an odd number?
After completing a similar discussion, write Even
Numbers and Odd Numbers above the appropriate
columns in the table.

Teacher: Think about how we use the words "even" and
"odd" in our everyday language and see if you can figure out which column has even numbers and which column has odd numbers. Who wants to share their ideas
with the class?
Luis: I think four is even.
Teacher: Why do you think four is an even number?
Luis: Four makes pairs.
Teacher: We used four cubes to represent the number four
and we can build two pairs. Why do you think two pairs
of cubes is an even number of cubes?
Grace: When we say even, it's the same. We made pairs that
are the same.
Teacher: So…the pairs for four are the same, each pair has
two cubes. Grace and Luis say that if we can make
pairs, the number is even. Would someone else like to
share an idea?
Nila: I think Grace is right.
Teacher: If they are even, then what would make other numbers odd?
Jerome: Are they weird?
Teacher: That is one way we use the word odd, but there is
some way that odd numbers are different from even
numbers. Look at the numbers your classmates have
built. What do you notice?
John: Some of the numbers don't have pairs.
Teacher: Some of the numbers cannot be built with pairs of
cubes. They always have one left over that is not in a
pair. Look at our table to see where these numbers are.
These are the odd numbers. I will write Odd Numbers in
the column that says Numbers with a Leftover Cube,
and I will write Even Numbers in the column that says
Numbers with Only Pairs of Cubes.
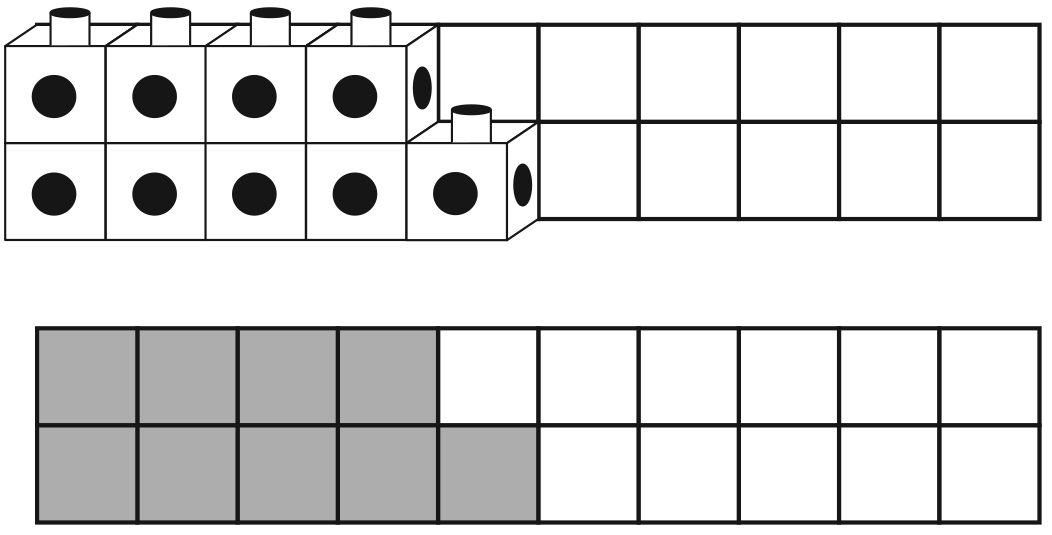
Representing Numbers with Models.
Display nine connecting cubes randomly and ask:
- Is there an even number or an odd number of
cubes showing? How did you decide?
Rearrange the nine cubes on one of the grid strips
from the Strips Master. See Figure 4.
- Is there an even number or an odd number of
cubes showing? How did you decide?
- Are all the cubes in pairs? Why or why not?
Now display 8 connecting cubes (4 in each row) and ask:
- Is there an even number or an odd number of
cubes showing? How did you decide?
- Are all the cubes in pairs? Why or why not?
With a different grid strip from the Strips Master,
color in 11 squares (5 in one row and six in the
other).
- Is there an even number or an odd number of
cubes showing? How did you decide?
Repeat with other numbers.
Assign each student a different number by distributing the self-adhesive notes you prepared to each person in the classroom. Give each student one grid
strip from the Strips Master if their assigned number
is less than 20 and two if their assigned number is
greater than 20. Tell each of them to write their number on the back of their grid strips and represent their
numbers by coloring in pairs of boxes following the
examples you already demonstrated.
After students
have had a chance to complete the task, ask partners
to check each other's work:
- Does the number of cubes match the assigned number?
- Is the strip colored to show the leftovers?
Even or Odd Bubble Sort. Students previously performed a Bubble Sort in Unit 1 Lesson 5. As a
reminder, review the concept of a bubble sort.
Ask students to come to the front of the room with
their strips and their self-adhesive note and conduct
a Bubble Sort. Ask students with numbers 1–10 to
line up near the left side of the room. Students with
numbers over 10 should line up near the right side of
the room.
When you say, "compare," adjacent students compare their numbers and make adjustments. If the student pair is already in order, they stay in place.
Remind students they are just comparing and switching with the student next to them until the teacher
says "compare" again. Repeat until no more
switches need to be made. Students will have placed
themselves in order according to their assigned number.
- Now that you are in order, let's say our numbers out loud beginning with one.
- Look at your number. Do you have an even or an odd number? How do you know?
- If you have an even number step forward. Who has the first even number?
- What do you notice about the even numbers? (Every other number, starting with two, is even.)
- What do you notice about the odd numbers? (Every other number, starting with one, is odd.)
Focus students' attention on the class number line.
Ask students to identify the even and then the odd
numbers on the number line. Students should notice
the alternating pattern.
Focus students' attention on the Even and Odd Chart on display.
- If we start with one and place the numbers in the
appropriate columns in the chart in order, what will
happen? (The numbers will be placed in alternate
columns starting with odd numbers.)
Ask students to place their grid strips and their self-adhesive note representing their assigned number on
the Even and Odd Chart. Students should notice that
they will alternate between the even and odd
columns. See Figure 5.
For students who have numbers greater than 20, tape
two strips together end to end.
Even or Odd. Since we have based our definition of an odd
number on whether there are any leftovers after pairing,
children might question whether one is odd or even since
there are no pairs at all. Point out that, with or without a
pair, there is still one left over. Along the same lines, they
may question whether zero is odd or even. Zero is even,
since there are none left over.