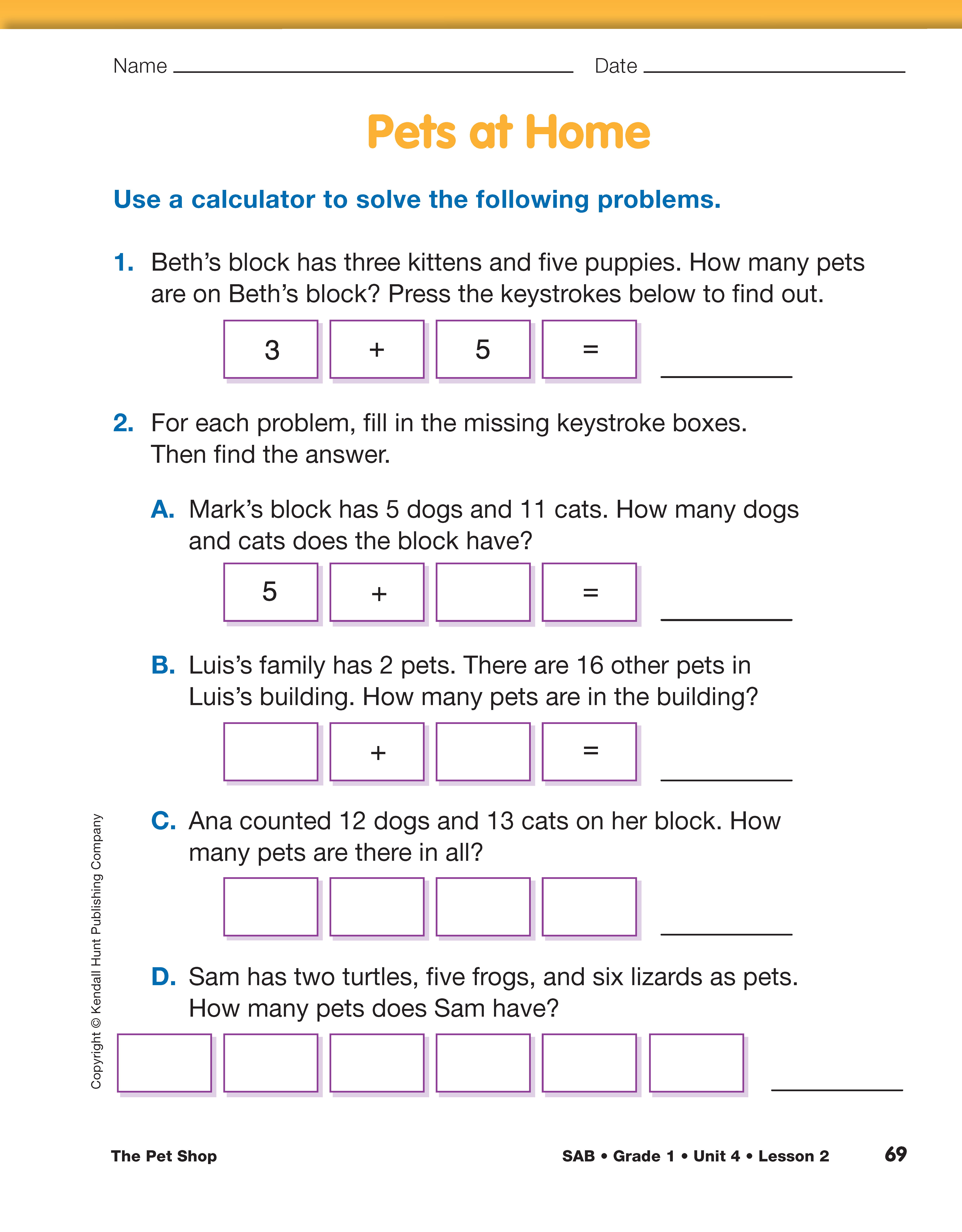
The Pet Shop

Est. Class Sessions: 2

Developing the Lesson

Part 2: Using Calculators

Introduce the Calculator. Display the Math Practices page from the Student Activity Book Reference section. Remind students that it is important to choose good tools for solving problems [MPE2]. Explain that calculators are tools that can help with mathematics. They are tools that students can use to check their calculations and to see if their answers to problems are reasonable. Remind students that these are also important Math Practices [MPE4, MPE3]. Refer again to the story problem where Mark wants to buy four bunnies, three lizards, and six kittens. Display the following keystrokes:

Explain that to solve this problem, students could press these keystrokes on the calculator. Help students connect the keystrokes pressed to the numbers they represent in the story.

Ask:

Does the list of keystrokes look like a number sentence? Explain. (Yes, there are numbers and symbols that show what we need to add together to find the total number of pets Mark wants to buy.)
What does the 4 stand for? (4 bunnies)
What does the 3 stand for? (3 lizards)
What does the 6 stand for? (6 kittens)
What other keystrokes are shown? (the plus sign and the equal sign)
Why do we need to press those keys? (The plus tells the calculator to add and the equal sign tells the calculator it is time to find the total.)
Could we press the keys in a different order and get the same answer? (You could start with a 3 or a 6, but you must put a plus sign in between numbers you are adding together.)
What key must be pressed last? (equal sign)

Emphasize to students that the calculator will compute the total and display a number that makes the number sentence true. Both sides of the equal sign in the equation will result in the same amount. Some calculators have an equal sign that locks in the constant meaning each time the equal key is pressed, the calculator will perform the last operation. Therefore, it is important to emphasize that students should hit the equal key only once. If they happen to press the following keys:

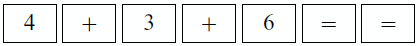
then the calculator will give them the wrong answer. If students list the correct keystrokes and the answer is incorrect, they might have pressed the equal key more than once. Students may ask what to do if they press a wrong button. For now, tell students to clear the calculator or turn it off and on again to start over.

Use Calculators to Solve Problems. Distribute calculators and ask students to turn them on. Display problem 13 + 6 =.

Ask:

Do you predict the answer will be more than 10? Less than 10? About the same as 10? (Possible response: I think it should be more than 10 because when I look at my number line, 13 is already more than 10.)
Is there a key on the calculator with a 13 on it? (No)
How can we enter these keystrokes? (Press the 1 key and the 3 key to make a 13, then the plus key, then the 6 key, and then the equal key.)

Have students use the calculator to solve the problem. Complete the problems on the Pets at Home page together by assisting students in reading the problems. The intention is to give students the experience of reading keystrokes and then pressing them. Help them write the keystrokes in the boxes on the page as needed. As students become more comfortable with the calculator, encourage them to independently write the keystrokes used to find each sum.

Challenge students to use the calculator to find the total number of pets in the picture on the Animals in the Pet Shop page and to list their keystrokes.

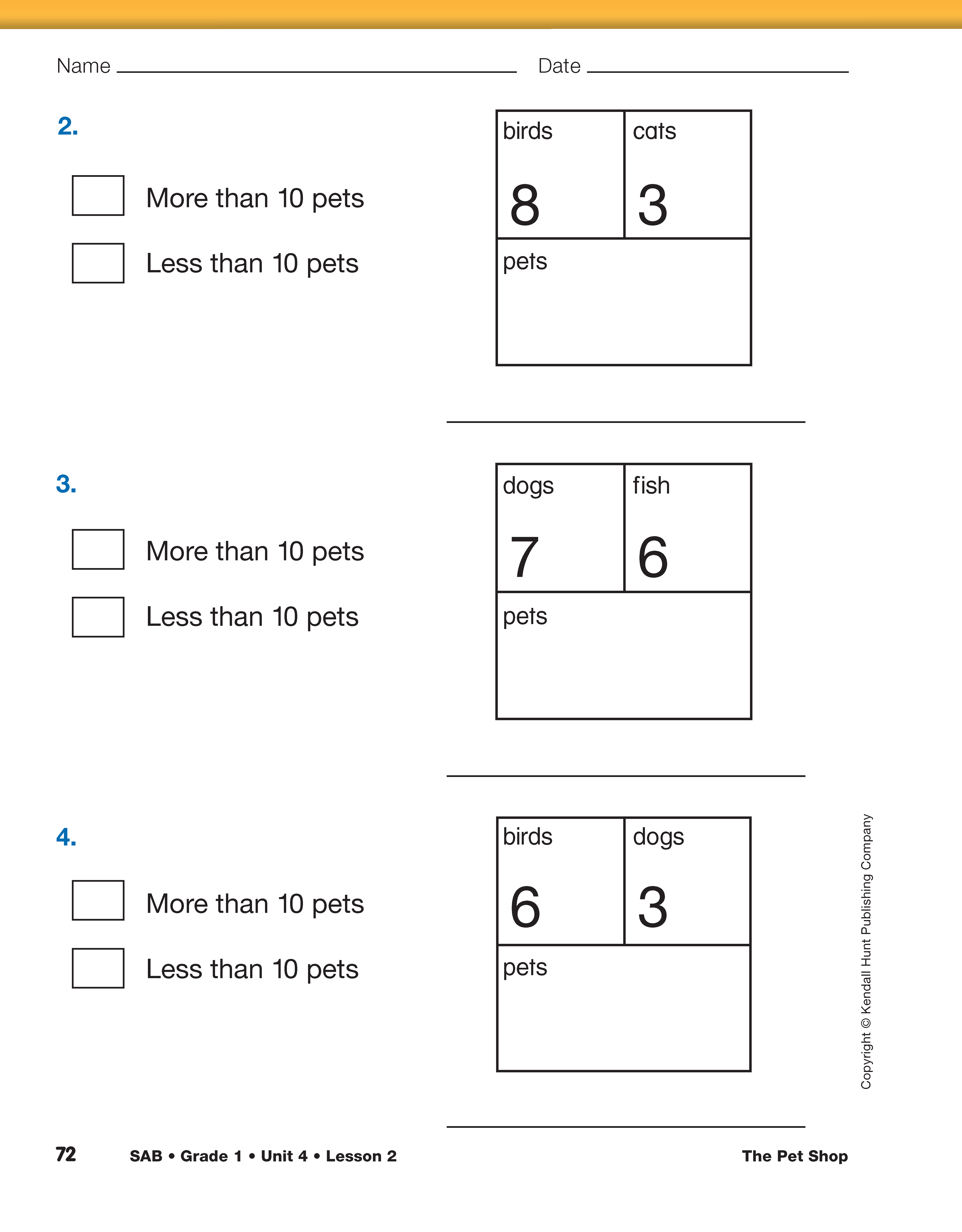
Estimate Sums.

Ask:

There were 5 dogs and 3 cats in the pet parade. Were there more than 10 or less than 10 pets in the parade?
Show or tell how you decided on this estimate.
Solve the problem and then use your estimate to help you decide if your answer is reasonable.

Have students share their estimation and solution strategies. If someone doesn't suggest it, encourage students to think about a ten frame when estimating. Show students how 5 dogs would fill the top row and 3 cats would fill only part of the second row, so the total is less than 10. Other students may reason that 5 plus 5 makes ten, and since 3 is less than 5, the answer will be less than 10. Students should decide whether their answers are reasonable based on their estimation of a sum greater than or less than ten. See Content Note.

Determining the Reasonableness of a Solution. In this lesson, students begin to use calculators as computational tools, and at the same time, to consider if their answers make sense. "Estimating is… a practical skill. It can guide students' use of calculators, especially in identifying implausible answers, and is a valuable part of the mathematics used in everyday life" (National Research Council, 2001).

A good practice is for students to make an estimate before solving the problem and then to look back to see if the answer makes sense after solving the problem. "The accurate and efficient use of an algorithm rests on having a sense of the magnitude of the result. Estimation techniques enable students not only to check whether they are performing an operation correctly but also to decide whether that operation makes sense for the problem they are solving" (National Research Council, 2001).

These habits of mind will take time to develop. It is important to encourage and reward students' early steps toward developing these habits and let students find for themselves the most productive way to think about the reasonableness of their solutions. Students should not see these steps as extra tasks imposed by the teacher but as an intrinsically useful part of the problem-solving process. The questions of when and how they think about the size of their answers are not as important as that they do it. "Children must learn to trust their own abilities to make sense of mathematics" (NCTM, 2000).

As a gentle introduction to determining the reasonableness of a solution, at this point we simply ask students to consider whether the answer to an addition problem should be more than or less than ten. For example, a student may reason that 9 + 5 must be more than 10, since 9 is only one away from 10 on the number line and 5 more would make it go past 10.

Direct students' attention to the Pet Problems pages. The pages feature a part-whole diagram. Complete the first problem together, then assign the remaining problems to student pairs. Partners decide if the answers should be more than ten or less than ten. Then one partner solves the problem choosing any of the available tools, except a calculator, including connecting cubes, number line, ten frames, and counters, and writes a number sentence. The other partner solves the problem using a calculator. Partners compare answers and agree on a correct solution. Finally, students should look back at their estimate and decide if their answer is reasonable. Partners should take turns using the calculator and solving the problems.