Parts and Wholes

Use Two Parts to Make a Whole. Read the book 12 Ways to Get to 11 by Eve Merriam aloud to the class. It presents varied addition situations for the number 11, ranging from simple to complex. The book provides a starting point for partitioning a whole into parts and for understanding a whole as the sum of its parts. As you read the book, ask students to explain how the "parts" on each page can be combined to make the "whole," 11. Encourage students to use a counting-on strategy when discussing the addition situations on each page.

After reading the book, distribute eleven connecting cubes to each student. Display the Two Parts and the Whole Master and post the Ways to Make 11 chart you prepared prior to the lesson. See Materials Preparation.

Use cubes or counters to demonstrate how to represent this problem with the part-whole diagram on the display of the Two Parts and the Whole Master.

Move the cubes from both "parts" into the "whole" section. Do not show cubes for both the parts and the wholes at the same time on the diagram. Some students may become confused and add everything together showing a total of 22 cubes. The point is to show the equivalence between the parts and the whole, that 9 + 2 is equivalent to 11, and that nine and two are parts of eleven, not separate entities.

Write words to describe the addition situation on the Ways to Make 11 chart: "Pick up nine pinecones and two acorns. I have eleven things from the forest." Write the number sentence 9 + 2 = 11 near it so students can connect the different representations of the numbers. See Figure 2.

Tell students that you are going to write the number sentence a different way. See Content Note. Write 11 = 9 + 2 on the chart.

Using the display of the Two Parts and the Whole Master, show students 11 cubes in the "whole" section. Then move 9 cubes into one "part" section, and 2 cubes into the other "part" section. See Figure 3. Have students use their cubes to perform the same process.

Add 11 = 9 + 2 to the Ways to Make 11 chart. Repeat this process with other examples of two-part partitions. From the book, 12 Ways to Get to 11, use the pages with six circus peanut shells and five popcorn pieces, and the pages with one sow and ten piglets. Have student volunteers demonstrate how to show the partitions on the display of the Two Parts and the Whole Master as other students work with their cubes at their desks. Continue to add words and number sentences to the chart.

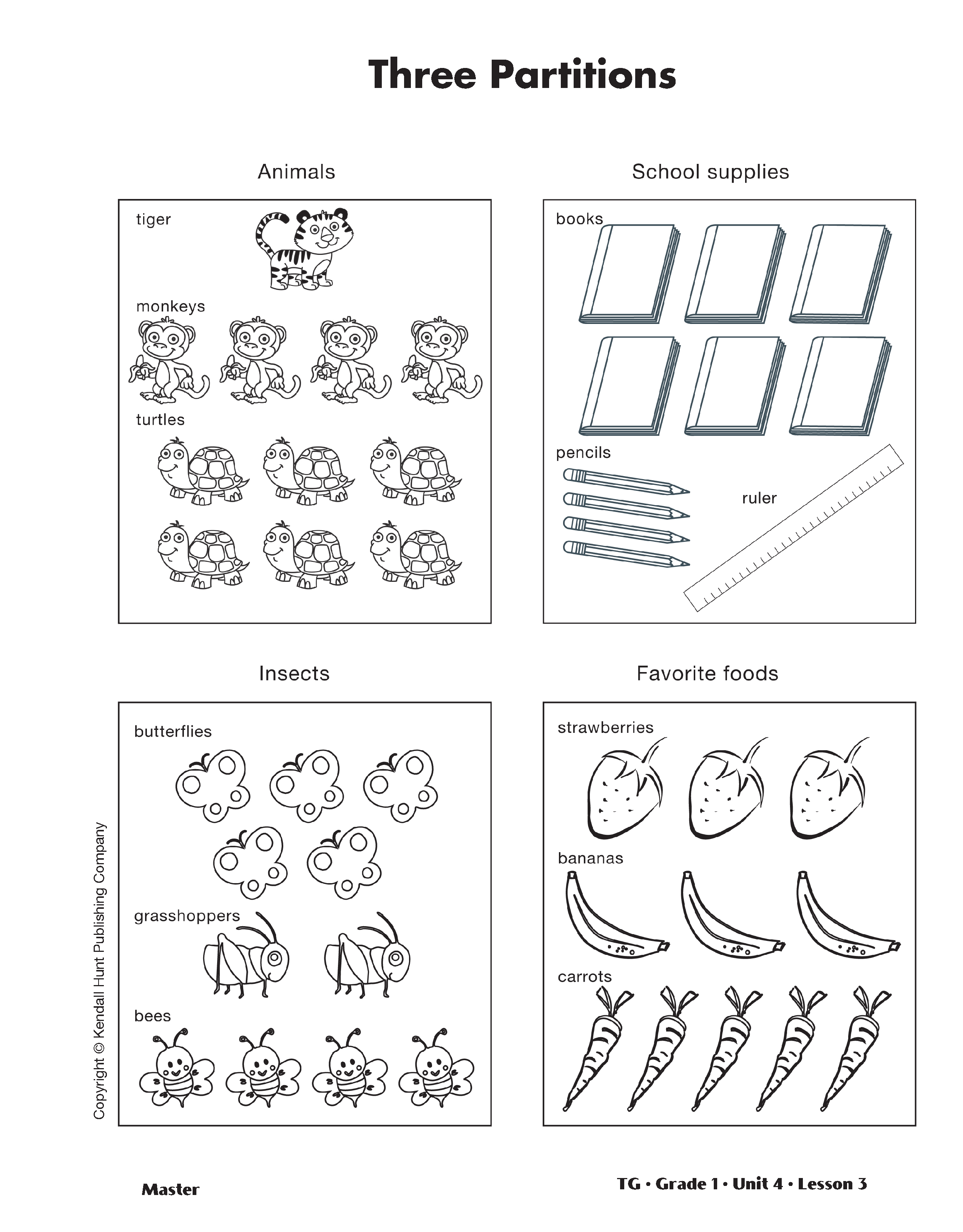
Use Three Parts to Make a Whole. Display the Three Partitions Master. Use one of the drawings to create an addition sentence with three addends. For example, write "I have 6 books, 4 pencils, and 1 ruler in my desk" on the Ways to Make 11 chart.

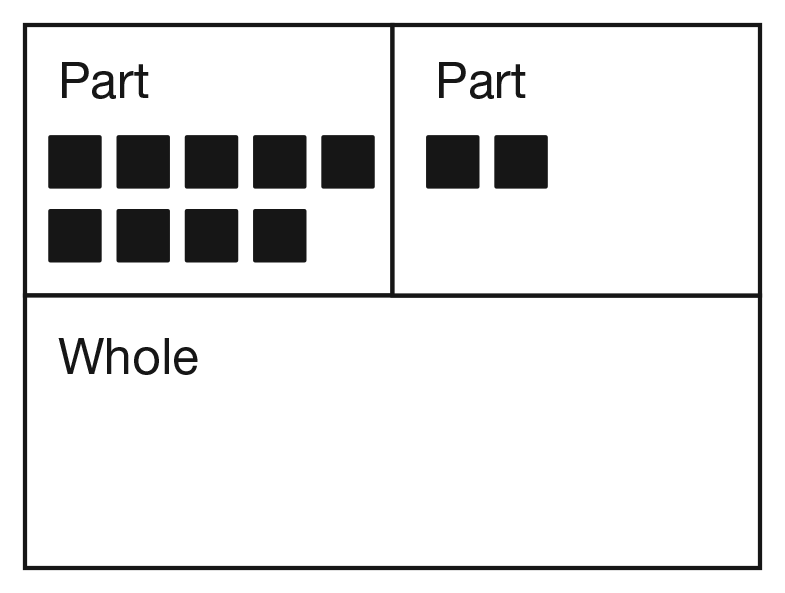
Use cubes to demonstrate how to represent this problem with the part-whole diagram on the Three Parts and the Whole Master.

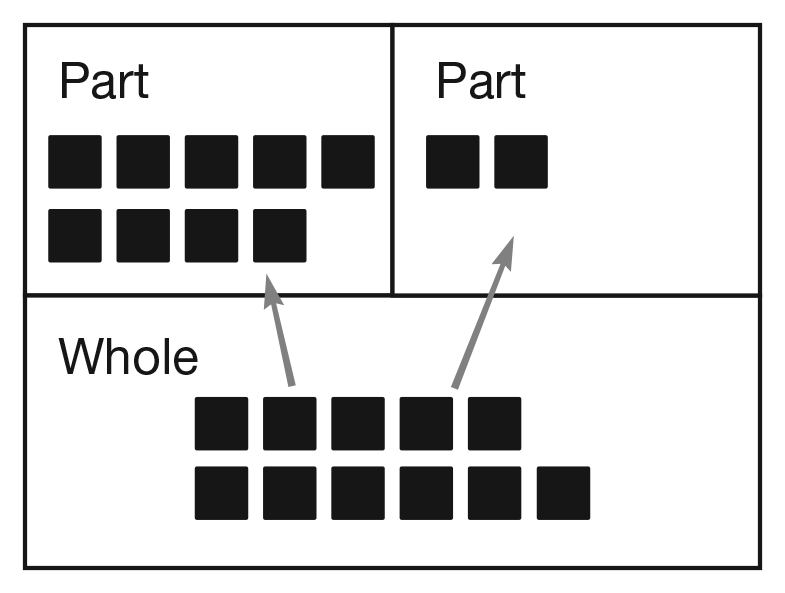
Move the cubes from the three "parts" sections into the "whole" section. Write the numerals 6, 4, and 1 where the cubes were as shown in Figure 4.

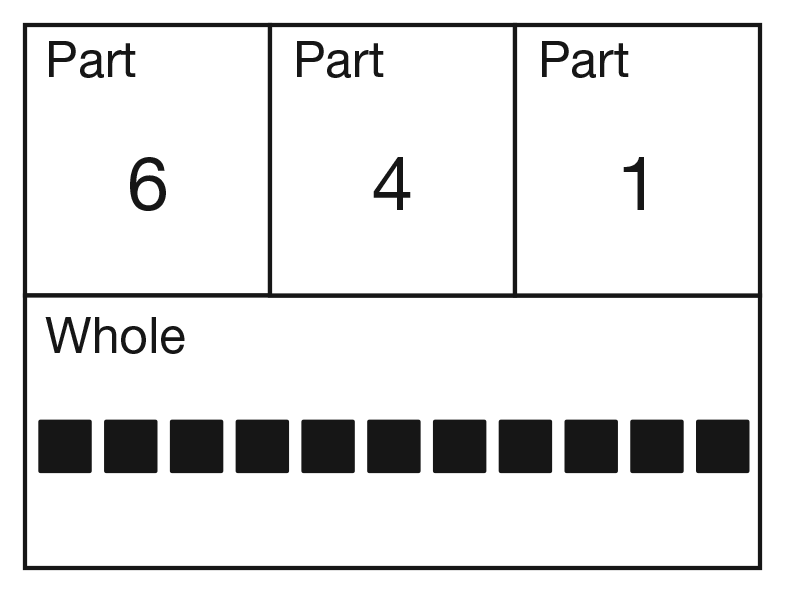
Remove the 11 cubes from the "whole" section and write the numeral 11 in their place. Write 6 + 4 + 1 = 11 and 11 = 6 + 4 + 1 on the Ways to Make 11 chart. See Figure 5. Explain to students that sometimes there are three groups of things to put together, or three parts combining to make the whole. Remind students that in the book, the author even has groups of 4 and 5 different things that she puts together.

Student pairs can refer to a display of the Three Partitions Master as they create another addition situation that shows a three-part partition of 11. They should continue to use their connecting cubes and write number sentences to match the word sentences. Add students' word and number sentences to the Ways to Make 11 chart. Remember to write the number sentences both ways.

Partition 12. Direct students' attention to the Parts and Wholes pages in the Student Activity Book. Have students write "12" at the top of the page. Each student pair should have 12 cubes or counters to work with. Students put their cubes in two or three piles and record how many are in each pile by writing numbers in the diagrams on the page. Students describe the parts and the whole by writing a number sentence. See Figure 6.

Post the Ways to Make 12 chart. When students have finished the page, have them cut along the dotted lines to separate each problem. Randomly distribute the sheets of paper to students and have them check the number sentences on the page using a number line, connecting cubes, a calculator, or counters. If the number sentences on the papers are correct, have students tape or glue them to the chart.