Adding to Solve Problems
Part-Whole Model for Addition
This unit focuses on the connection between real-world situations and addition. It emphasizes … read more
Part-Whole Model for Addition
This unit focuses on the connection between real-world situations and addition. It emphasizes writing number sentences for problems and developing the everyday and mathematical language associated with addition. This helps children solve problems by relating word problems to appropriate operations. One important aspect of identifying addition situations is interpreting a situation in terms of "parts" and "wholes." That is, we add when the parts are known and the whole amount is unknown.
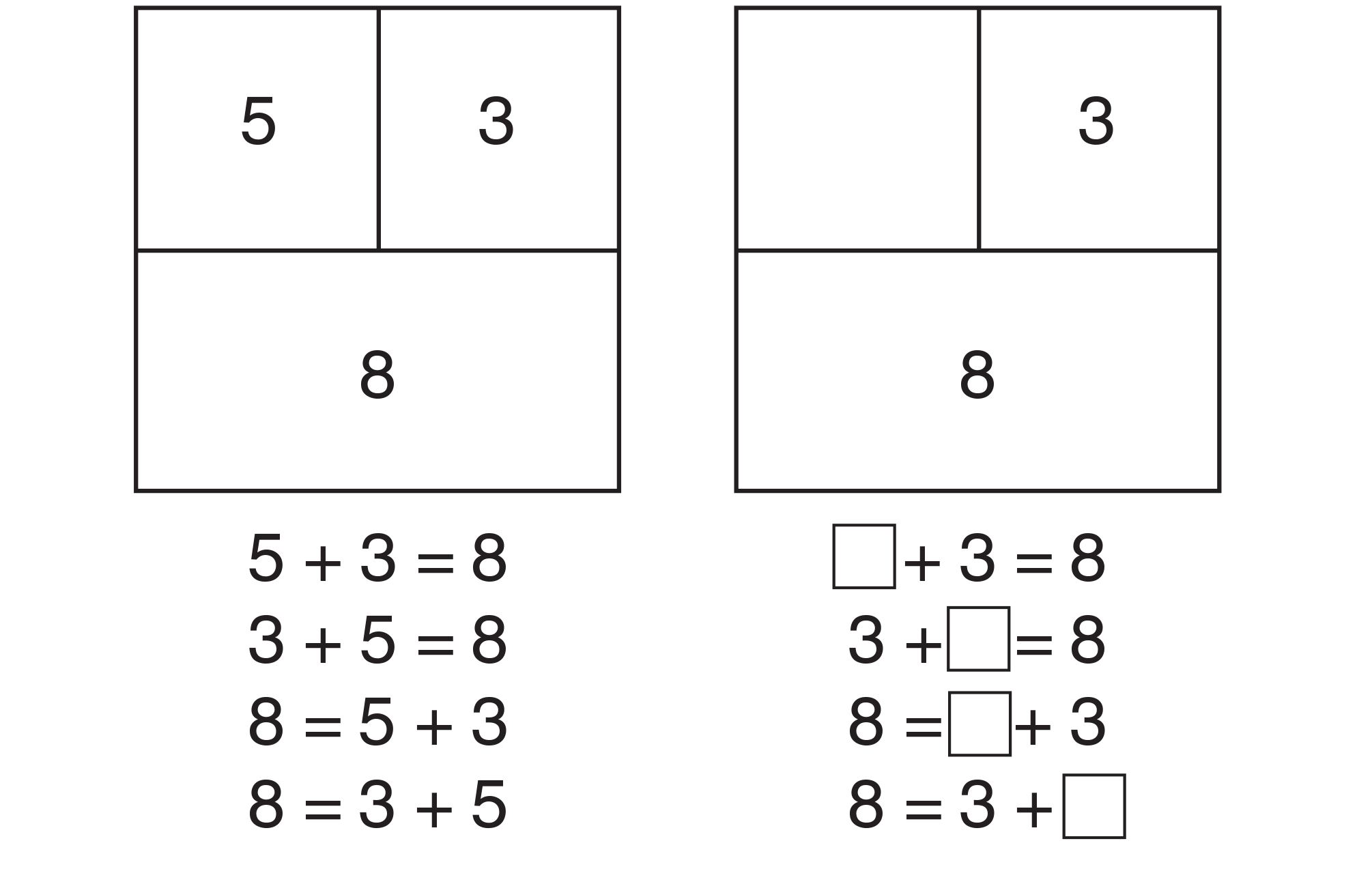
Figure 1: Part-whole diagrams and corresponding
addition sentences
The part-whole model, introduced in Unit 3, is a visual model showing that two partitions of the whole can be represented by various number sentences. Questions such as "If I have 5 pennies in my shirt pocket and 3 pennies in my pants pocket, how many pennies do I have in my pockets?" can be written as 5 + 3 = 8, or as its turn-around sentence 3 + 5 = 8. See the first diagram in Figure 1.
It is also important for students to see number sentences in which the total comes first (8 = 5 + 3, 8 = 3 + 5). In this way students are more likely to develop strong concepts of equality instead of acquiring the notion that the equal sign means that "the answer comes next."
Missing Addend Problems
In this unit, "missing addend" problems are also introduced. For example, "I have 8 pennies … read more
Estimation and Number Sense
In this unit, "missing addend" problems are also introduced. For example, "I have 8 pennies in my pockets; there are 3 pennies in my pants pocket; how many pennies are in my shirt pocket?" can be written as + 3 = 8 and represented in a diagram as shown in the second diagram in Figure 1. Some students will see this as an addition problem and will do some form of counting on to solve it. Others will see it as a subtraction problem (8 − 3 = 5). Either approach is correct and should be accepted. In later units, students will come back to this same visual model and conceptual framework as they formally study subtraction.
Counting On
The unit revisits the counting-on strategy to find a sum. Figure 2 shows several different way … read more
Counting On
The unit revisits the counting-on strategy to find a sum. Figure 2 shows several different ways to model the counting-on strategy for 5 + 3 = 8. Some students will need extended time and multiple opportunities to use counting on before it is natural for them.
Counting on is one of several strategies that help students learn addition facts and develop more mature ways of thinking. Throughout this unit, counting on is emphasized so that students will learn to use it as a legitimate strategy for finding sums. This strategy is promoted by hiding one group of objects from view and by using other situations in which it is more natural to use counting on than to count each individual object. For many students, it is just as efficient to count from one to solve the problem 4 + 2 as it is to use counting on. However, it would be cumbersome to count from one to add 26 + 2.
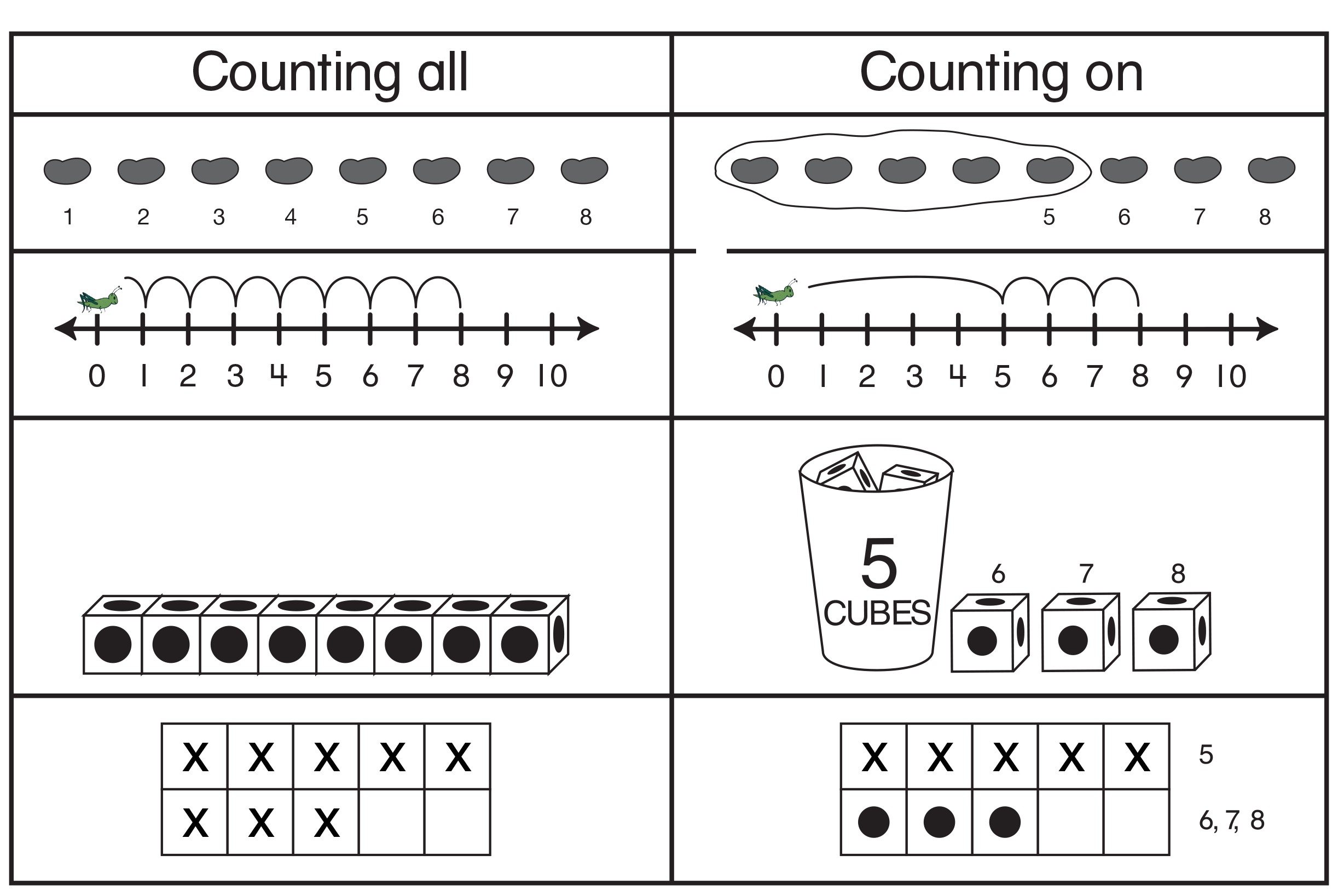
Figure 2: The difference between counting all and counting on to solve 5 + 3 = 8 as shown by several models
“Encouraging children to use efficient strategies to derive unknown facts before drill is better than 'premature drill' … and doing so increases both initial learning and retention.”
C.A. Thornton, "Strategies for the Basic Facts," Mathematics for the Young Child, NCTM, 1990.
Developing Strategies for Addition Facts
Generally, students move through three development stages when acquiring operational understanding … read more
Developing Strategies for Addition Facts
Generally, students move through three development stages when acquiring operational understanding and fluency with the math facts.
- Direct modeling in which students re-create the action;
- Counting strategies such as counting on and counting back; and
- Reasoning from known facts in which students work from facts they already know. For example, if a student knows that 6 + 4 = 10, then he or she has a quick way to access 6 + 3 = 9 (Carpenter, 1999, National Research Council, 2001).
Students need sufficient time to experience direct models and invent their own strategies for thinking about and solving problems involving math facts. In Math Trailblazers we emphasize the use of strategies and de-emphasize drill. Throughout the curriculum, students are encouraged to share their thinking when adding and subtracting. This emphasis on developing different ways of thinking about addition and subtraction before stressing rapid recall of facts is important.
Notes on Calculators
The calculator is introduced in this unit. This tool encourages students to explore number ideas and … read more
Notes on Calculators
The calculator is introduced in this unit. This tool encourages students to explore number ideas and relationships, enables them to solve more complex problems, and provides opportunities for exploring mathematics on their own. In subsequent units, we assume calculators will be available for solving problems.
In this unit, students connect keystrokes to the numbers in word problems. While solving problems with a calculator, they begin to develop the habit of deciding what kind of answer makes sense so they can decide if the answer they found with the calculator is reasonable.
Although most students have access to calculators at home, we recognize that some teachers and parents have concerns about allowing young students to use them in school. There is strong evidence that the thoughtful and purposeful use of calculators is a valuable educational tool for all students.
Discuss with parents why you are using calculators and how you plan to use them. Three important points to make:
- The calculator is a tool for doing mathematics—similar to pencils, counters, and manipulatives—and it is used to enhance and promote learning.
- The calculator will not be used to replace students' command of the basic facts or other ways of computing.
- When students use a calculator to solve problems, they should stop and consider whether their answers make sense.
“Instructional programs from prekindergarten through Grade 2 should enable all students to compute fluently and make reasonable estimates. … All students should use a variety of methods and tools to compute, including objects, mental computation, estimation, paper and pencil, and calculators.
“In the mathematics classroom envisioned in the Principles and Standards for School Mathematics, every student has access to technology to facilitate his or her mathematics learning under the guidance of a skillful teacher. … Technology can help students learn mathematics. For example, with calculators and computers students can examine more examples or representational forms than are feasible by hand, so they can make and explore conjectures easily.”
From the National Council of Teachers of Mathematics, Principles and Standards for School Mathematics, 2000.
Resources
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH. 1999.
- Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically: Integrating Arthmetic and Algebra in Elementary School. Heinemann, Portsmouth. NH, 2003.
- Falkner, K.P., L. Levi, and T.P. Carpenter. "Children's Understanding of Equality: A Foundation for Algebra." Teaching Children Mathematics, 6(4), p. 232, 1999.
- National Research Council. "Developing Proficiency with Whole Numbers." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Payne, Joseph N. Mathematics for the Young Child. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Professional Standards for Teaching Mathematics. National Council of Teachers of Mathematics, Reston, VA, 1989.
- Van de Walle, J.A., K.S. Karp, and J.M. Bay-Williams. Elementary and Middle Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc. Upper Saddle River, NJ, 2013.












