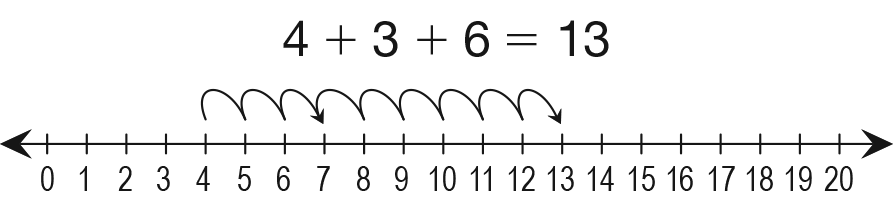Identify Quantities of Pets.
Students create and
solve problems based on the picture on the Animals
in the Pet Shop page. They should have connecting
cubes, counters, desk number lines, and copies of the
Ten Frames Master readily available so they can
choose from these tools to solve the problems. As
you distribute them, tell students that the Math
Practices page reminds us that mathematicians
choose good tools and strategies to help them solve
problems [MPE2].
Display the Animals in the Pet Shop page in the
Adventure Book, and direct students' attention to the
same page in the Student Activity Book.
- Describe what you see in this picture. Try to use
numbers in your descriptions. (Possible response:
I see four puppies in a box.)
As students make statements, write them on chart
paper using full sentences, as in "There are four puppies in a box" or "There are three puppies on the
counter." See Figure 1.
Write and Solve Addition Stories.
Use the statements to generate problems such as:
- How many puppies are there altogether? (7)
- Give a number sentence that shows the numbers
you put together to solve the problem.
(4 + 3 = 7 puppies)
- What does the 4 represent in this number sentence? (the number of puppies in the box)
- What does the 3 represent? (the number of puppies on the counter)
- What does the 7 represent? (the total number of
puppies in the shop, or all of the puppies in the
shop)
- Is this an even or an odd number? How do you
know? (odd; If I pair the puppies up, there will be
one puppy left over without a partner.)
- What does the + symbol mean? (add or put
together)
- What does the = symbol mean? (the same as; See
Content Note.)

Equal Sign. A common misconception is to think the equal
sign means "the answer is." Many students think the equal
sign means that they should solve the problem that comes
before it in the number sentence, and that the number after it
is the answer to the problem. Students at this level generally
do not see the equal sign as a symbol that means "is the
same as." The values on both sides of the equal sign are the
same. Thinking of a seesaw may help. In order for the seesaw
to be perfectly balanced, the weight on one side of the seesaw
must be the same as the weight on the other side of the seesaw. In order for a number sentence to be true, the amount on
one side of the equal sign must be the same as the amount on
the other side.
Students' understanding of the symbols in the number sentence will likely vary.
Allow time for discussion so that students can begin to develop an
understanding that the equal sign means "is the same
as" in a number sentence.
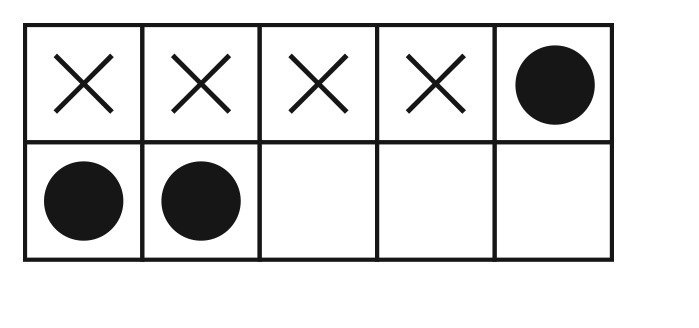
- How did you solve this problem? (Possible
response: I used a ten frame. I put in four Xs to
show the puppies in the box and then I put in
three dots for the puppies on the counter to make
7. I saw five on top and then 6, 7 on the next row.
See Figure 2.)
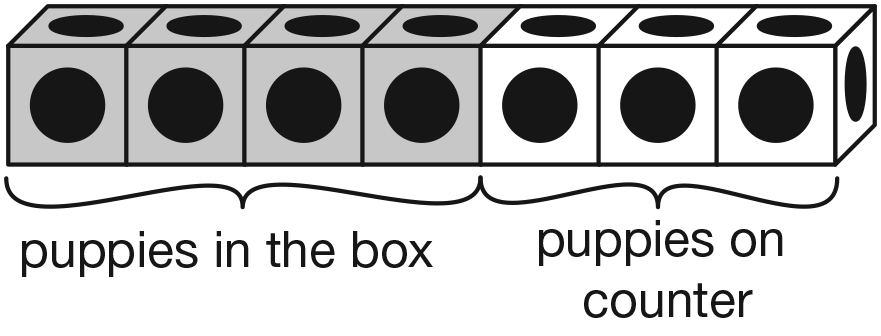
- Did anyone solve the problem a different way?
(Possible response: I used connecting cubes. I
made a train of 4 cubes to show the four puppies
in the box. Then I added 3 more cubes to show
the puppies on the counter. I started at 4 and
counted on 5, 6, 7. See Figure 3.)
As students report their answers and share their
strategies, write sentences in words that match the
number sentences, such as "Four puppies and
three more are seven puppies." See Figure 4.
To encourage students to listen to one another's stories, ask
one student to use the picture to make up an addition story.
Write sentences in words that match the story. Then ask a
second student to write a number sentence that matches the
story under your sentence as shown below.
I see four fish and one snail in the water.
There are five animals in water.
4 fish + 1 snail = 5 animals
Emphasize the Part-Whole Relationship.
Point to the four puppies in the box and indicate that they are
only part of all the puppies in the shop. Repeat this
as you point to the three puppies on the counter.
Then point to all seven puppies and indicate that
these are all of the puppies, or the whole group of
puppies. Note that there are other ways to say the
problem:
- Four and three more is seven.
- Four plus three is seven.
- Four and three makes seven.
- Seven equals four plus three.
Emphasize the parts and the whole in each problem.
If a student says, "I see five birds" (whole), encourage him or her to look for how many birds are in
each cage (parts).
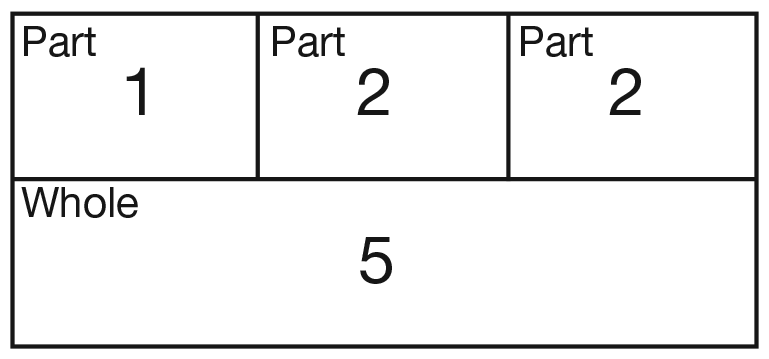
- How many birds are in each cage in the picture?
(There is one bird in one cage, and two birds
each in two more cages.)
- How many parts do you need to put together to
find the whole group of birds? (3 parts)
- How many birds are there in all? (5)
- How did you solve this problem? (Possible
response: I counted on. I started at 1 and counted
on 2, 3 and then 4, 5.)
- Give a number sentence that shows the numbers
you put together to solve the problem.
(1 + 2 + 2 = 5 birds)
- Why are there 3 numbers to add in this problem?
(There are birds in three different cages. There
are 3 parts in the whole.)
Use a part-whole diagram similar to those in Unit 3
to illustrate the problem. See Figure 5 for a diagram
that represents the total number of birds in cages.
Continue having students use the picture to generate
other addition stories about the animals. Record their
stories in words and write a number sentence for
each story on the chart paper. Ask students to share
their strategies. Make connections between the different representations of numbers.
Use Labels.
Take this time to informally introduce
the importance of using labels when solving problems. Display and refer students to the Math
Practices page in the Student Activity Book
Reference section. Tell students that mathematicians
use labels to show what numbers mean [MPE6]. In a
story where the animals added together are all the
same, labels are not as important. However, some
students may have written stories that combined different types of pets. For example, five birds and
seven puppies make twelve pets. Discuss labels such
as birds, puppies, and pets for these types of problems.
- Mark wants to buy four bunnies, three lizards, and
six kittens. How many pets does he want to buy?
Talk with a partner about how to solve this problem.
- How did you solve this problem? (Possible
response: We used counters. We counted out 4
for the bunnies, 3 for the lizards, and 6 for the
kittens. We put 4 and 3 together because we
knew 4 + 3 was 7 and then we counted on with
the other counters 8, 9, 10, 11, 12, 13.)
- Is this a reasonable solution? Does it make sense?
(Possible response: Yes. I thought about a ten
frame. 6 kittens would fill the first row with 5
and 1 more would go into a box on the second
row. 4 bunnies would fill that row for 10 pets
total so I know the answer has to be more than
10. If I add the 3 lizards on, it is 13.)
- How could we check the answer? (Possible
response: We could use the number line. Start at
4 and move forward 3 to 7. Then from 7 move
forward 6 to 13. See Figure 6.)
- Write a number sentence that matches the solution. (4 + 3 + 6 = 13)
- How can we clearly show what these numbers in
the number sentence mean? (Add the labels bunnies, lizards, kittens, and pets.)
Write "4 bunnies + 3 lizards + 6 kittens = 13 pets"
so that students can see how labels make solutions
clearer.
Assign the Animal Addition Stories Homework
Master after Part 1. Remind students to add labels to
show what the numbers in their number sentences
mean. They can use pictures or words as labels.