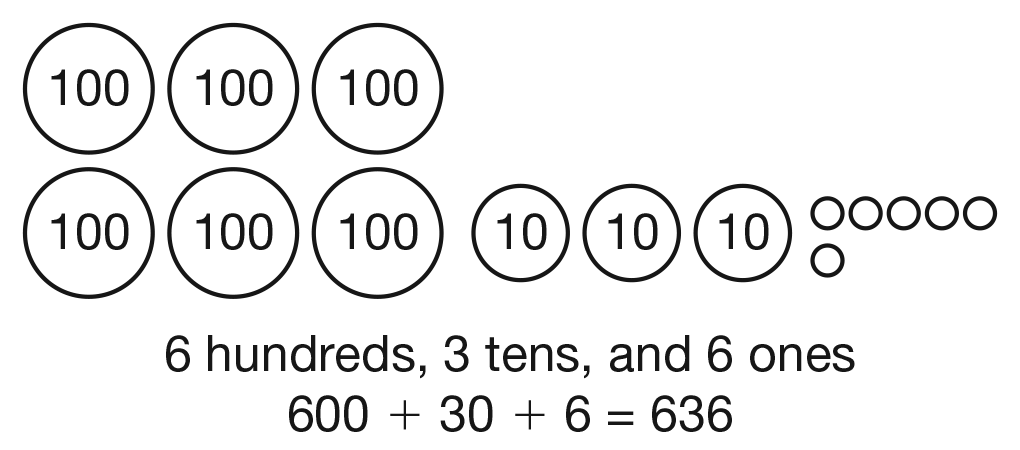Estimate the Total Number of Buttons.
Show students
the collection of about 1000 buttons in a clear
container. Give student pairs a minute or so to talk
with their partner about how to estimate the number
of buttons in the container. Remind them to refer to
the benchmark bags of 20, 50, and 80 buttons displayed
on the class number line. Have pairs write
their estimates on an index card or self-adhesive
note, along with their names. Have students put
these estimates in a safe place or collect them in one
place on the board.
-
During our first lesson with buttons, each group
estimated the number of buttons in their bags.
How did you make your estimate? (Possible
answer: We used the benchmark bags to help us
make an estimate.)
-
Look at the total number of buttons in this jar and
look at the benchmark bag of 80 buttons. Are there
more or less than 80 buttons in the jar?
-
What else could we use to make a good estimate?
(Possible response: When we estimated our small
bags on the first day, we had 74 buttons in our
bag. We can compare our bags to the class collection.
We know there is a lot more than that number.)
Group and Count Buttons. Ask students to think of
efficient ways to group and count the collection of
buttons. Students will likely decide that groups of
ten are easy to count. Model putting ten buttons in a
cup.
-
If I fill two cups, each with 10 buttons, how many buttons would I have? (20)
-
How many tens would that be? (2 tens)
-
How can I write that as a number sentence?
(10 + 10 = 20)
Hold up two cups of ten buttons and say:
- 1 ten, 2 tens. Ten, twenty.
- How many buttons in three cups? (30) How many tens? (3 tens)
- How can I write that as a number sentence?
(10 + 10 + 10 = 30)
Ask students to look at Question 1 on the Button Place Value page in the Student Activity Book.
Read the problem and ask:
- Why did John stack the cups of buttons? (To show ten groups of ten or 100 buttons.)
- How many groups of 100 does John have? (1 group of 100.)
- How many groups of 10? (1 group of ten)
- How many ones? (2 ones)
- Write a number sentence to show how John’s buttons are grouped. (100 + 10 + 2)
Divide the class into groups and distribute the buttons
and ten paper cups. Be sure all the buttons are
distributed. Direct students to group the buttons by
tens using the cups.
When the groups fill ten cups, ask:
-
How many buttons are in ten cups? (100)
-
How do you know? (Possible response: If we count by tens, we’ll get to 100.)
-
How can I write that as a number sentence?
(10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 100)
The size of the student groups will depend on the size of your
class. Some teachers prefer students work in groups of 2 or
3 students. Others have organized the class into 5 groups of
students and given each 15 of the collection of buttons. Be
sure each group is asked to group and count at least
100 buttons.
Have the rest of the class observe as you help the
first group pour the ten cups of ten buttons into a
plastic bag and rename the group 100. Have the students
count by tens with you as the cups are emptied.
-
How many buttons are in this bag? (100)
-
How many hundreds are in this bag? (1)
Distribute one bag to each group and ask them to
continue to group and count their buttons. Each bag
should hold 100 buttons and each cup 10 buttons.
Help students work cooperatively by encouraging them to
have each member of the group count 10 buttons per cup
and then take turns pouring the ten cups of buttons into the
plastic bag as group members count aloud by tens. Each
member of the group should record their group’s totals on
their Button Place Value page in the Student Activity Book
and check each other’s work. Group members can also
decide who will record the total number of buttons on the
chart paper and who will bring leftover ones and tens to the
front of the room when the class finds the total in the
collection.
When the cups are empty, students can use them to
make additional groups of ten. If a group has more
than 200 buttons, give them a second plastic bag.
Explain to students that when they finish grouping
all their buttons, they may have cups of ten left over
that do not make a hundred and single buttons left
over that do not make a ten. When all the buttons
have been placed into groups of hundreds, groups of
tens, and ones left over, ask students to complete
Question 2 on the Button Place Value page in the
Student Activity Book. Use the display of the Button
Place Value page to model how to draw a picture
and record their answer.
As you circulate, pay attention to how students are
recording their counts. Note that they should record
the number of hundreds, tens, and ones. If a student
records “100” for the groups of hundred, ask him or
her to show you how many hundreds he or she had.
Count each hundred (in the plastic bags) along with
the student. Guide students to recognize that 2 plastic
bags of buttons represent 2 groups of hundreds,
not 200 groups of hundreds, so the number 2 indicates
the number of hundreds, not 200. When all the
groups have recorded their totals on the Button Place
Value page, have each group write their total number
on chart paper.

Observe students as they complete Check-In: Questions 1–2
on the Button Place Value page in the Student Activity Book
to assess their abilities to represent and identify quantities
(e.g., greater than 100) using drawings, symbols, number
sentences, and words [E1]; use and apply place value
concepts to make connections among representations of
numbers [E2]; and use efficient grouping strategies to count
a collection of objects [E3].
Place the Scoop and Group Master and a container of
counters and a scoop in a learning center for students who
need additional practice with grouping, counting, and
representing larger quantities.
Combine Group Totals.
To find the total number of buttons in the class collection, ask:
-
How can we find the total number of buttons in the class? (Possible response: Combine all the leftover
buttons, and then find the total number of hundreds, tens, and ones.)
Have students bring their leftover ones to the front of the room.
-
We have this pile of leftover buttons. How many groups of ten are there? How can we find out? (We can group and count all the leftover buttons.)
-
What number sentence can you write to show the groups of ten and leftover ones? (Possible responses for the number 36: 30 + 6; 10 + 10 + 10 + 6)
Combine individual buttons to make additional cups
of ten. Have the class count them aloud with you.
Next have students bring their leftover cups of ten to
the front of the room.
-
We have [13] cups of ten. How many groups of ten do we have? (13 groups of ten)
-
What number sentence shows the groups of ten? (10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = 130 buttons)
- How many groups of a hundred do we have? (one group of a hundred)
- How can we find out? (Place ten cups of buttons in a plastic bag to make a group of a hundred.)
- What number sentence can you write to show the groups of one hundred and leftover tens? (Possible response for 130: 100 + 10 + 10 + 10; 100 + 30)
Combine ten cups of buttons to make additional
bags of 100, again ask the class to count along with
you. Ask students to draw a picture in Question 3 to
represent the tens and ones left over. See Figure 2
for a sample showing that there are 6 groups of 100,
3 groups of ten, and 6 leftover buttons.
Finally, have students bring their bags of 100 to the
front of the class. Have the class count them aloud
with you.
If there are more than ten bags of 100 in your class collection, ask:
- How many buttons are in 10 bags of 100? (ten hundred or 1000)
- How do you know? (Possible response: If we count by 100, we’ll get to 1000.)
Explain that ten hundred is the same as 1000.
When counting groups of hundreds, tens, and ones left over,
it is important for students to first see the groups as bundled,
such as 12 groups of ten, rather than immediately re-bundling
and recording it as 1 group of one hundred and 2 groups of
ten. Students need to see the groupings in various partitions
to help them develop the concept of the hundreds, tens, and
ones as separate units in our base-ten system. This facilitates
not only an understanding of base-ten units but also helps
develop a conceptual mental image of large quantities.
Ask students how many groups of hundreds, tens,
and ones are in the class collection. Have students
draw the groups of 100 and write a number sentence
to match the number of hundreds, tens, and ones.
Ask questions similar to the following:
- How many hundreds do we have? Tens? Ones?
- What number sentence can you write to show the groups of a hundred, ten, and one? (Possible
responses for 768 buttons: 700 + 60 + 8 = 768; 100 + 100 + 100 + 100 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 8 = 768)
Have students record the groups of hundreds, tens,
and ones, and the number sentence for the total in
the class collection on the Button Place Value page.
Compare Buttons to Estimate. Next have students
compare their estimates with the actual number of
buttons. Ask them to think about whether their estimates
were close to the actual number, stressing that
good estimates are not expected to match the actual
quantity. Also emphasize that estimation skills
improve with practice and experience.
Compare Quantities of Buttons. Direct students’
attention to the group totals on the chart paper. Use
the display of the 200 Chart to help students compare
quantities of buttons less than 200. As groups
report their total number of buttons, have them find
the numbers on the 200 Chart and write comparison
statements.
Ask questions similar to the following:
- Group 1 has 136 buttons and Group 2 has 194 buttons.
Does Group 1 have more or less buttons than Group 2?
- How do you know? (Possible response: Group 2 has more because 194 comes after 136 on the number line.)
- What other tools can you use to show your thinking?
(Possible response: The 200 Chart can be
used the same way as the number line; I simply
compared the values. They both have one group
of 100, but 194 is 9 groups of ten not 3 groups of
ten. That makes it larger.)
- How can you write that using the symbols
> and <? (194 > 136 or 136 < 194)
- How are those statements read? (194 is greater
than 136 and 136 is less than 194.)
- Group 3 has 204 buttons. Group 4 has 196 buttons. Which group has more? (Group 3 has more.)
- How do you know? (204 is greater than 196.
Possible response: I know that 204 is greater than
196 because 204 has 2 hundreds and 196 has
1 hundred; I used the 200 Chart and 204 is not
even on there, it is off the chart so it must be
larger than 196.)
- How can you write that using the symbols > and <? (204 > 196 or 196 < 204)
- How are those statements read? (204 is greater than 196 or 196 is less than 204.)
Ask students to use greater than (>) or less than (<)
symbols to compare group totals. See the Sample
Dialog for a class discussion about comparing numbers.

Use the Sample Dialog to guide your class discussion of
comparing numbers with hundreds, tens, and ones.
Teacher: Our class has 34 single buttons left over. How can
we combine these buttons to show how many tens and
ones are in 34?
Peter: We can keep putting ten buttons in cups until we don’t
have enough to fill a cup of ten.
Teacher: Good! Peter, start filling cups of ten and let’s
count with him.
Peter: [after filling the cups of 10] I filled 3 cups of ten and I
have 4 left over. I shouldn’t put the 4 buttons in a cup or
I’ll make a mistake and count it as a ten.
Teacher: Great job, Peter! Who can tell us what 34 ones is
equal to?
Suzanne: 34 ones is the same as 3 tens and 4 ones. That’s
what Peter just showed us by putting the buttons in
cups of ten and keeping the leftover buttons outside the
cups.
Teacher: Good thinking, Suzanne. What is a number
sentence to show what we just did?
Faith: 10 + 10 + 10 + 4 = 34. We can combine the tens and
say 30 + 4 = 34.
Teacher: Excellent, Faith. Now let’s gather the cups of ten
that are left over. We have 14 cups of ten. How can we
combine these tens to show how many hundreds we
have?
Javier: We can put them into plastic bags. Ten cups of 10
make 100.
Teacher: Good answer. Javier, start putting 10 cups of ten
into the plastic bag and we’ll count by tens with you.
Class: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Teacher: Do we have enough tens to fill another bag of
100?
Jason: No, we have only 4 left. We need 10 cups of 10 to
make 100.
Teacher: Okay, so we have 1 hundred and 4 tens. Who can
tell us how many tens is the same as 1 hundred and
4 tens?
Sarah: 14 tens! I get it now! 14 tens = 140.
Teacher: Great thinking, Sarah! What is a number sentence
to show what we just did?
Brandon: 100 + 10 + 10 + 10 + 10 = 140 or
100 + 40 = 140.
Teacher: Great! Now think about what we just learned and
tell us what 27 tens is equal to.
Sam: 27 tens is equal to 270.

If students are having trouble using the comparison symbols
appropriately, display a chart in the room that shows the
symbols and their meanings. Use the note in Question 4 on
the Compare Groups of Buttons pages as an example.
Students can also circle the smaller quantity and then insert
the symbol into the comparison statement. This will help you
determine if students are comparing the quantities properly
and using the symbols appropriately.
Have students work with a partner to compare quantities
as they answer Questions 1–4 on the Compare
Groups of Buttons pages in the Student Activity
Book. Have 200 Charts readily available and encourage
students to draw pictures to show their thinking.
Once students have had a chance to work on these
questions with a partner, discuss Questions 4J –N.
Show students the 138 counters you prepared. Tell
students that you are going to compare 138 to other
numbers. Use the counters and ten cups to decide
how to complete each comparison statement. Show a
group of hundred by stacking 10 cups of counters.
- Look the statement in Question J:
138  100 + 30 + 8. How did you solve this
problem? (Possible response: I first decided to
check to see if the number sentence was equal to
138 and it is.)
100 + 30 + 8. How did you solve this
problem? (Possible response: I first decided to
check to see if the number sentence was equal to
138 and it is.)
- How are the 138 counters grouped in Question K? (13 groups of ten and 8 leftover ones)
- How did you compare the quantities in Question L? (Possible response: 138 is less than 1 hundred and 38 tens.)
- How did you decide? (Possible response: 38 tens is equal to 380, so that quantity is obviously larger than 138 which has only 1 group of hundred.)
Assign the Groups of Hundreds, Tens, and Ones
pages in the Student Activity Book. Have the 200 Chart in the Student Activity Book Reference section
readily available.
Use the Groups of Hundreds, Tens, and Ones pages in the
Student Activity Book with the Feedback Box to assess
students’ abilities to represent and identify quantities (e.g.,
greater than 100) using groups of counters, drawings,
symbols, number sentences, and words [E1]; use and apply
place value concepts to make connections among
representations of numbers [E2]; and use words and
symbols (e.g., <, >, =) to show comparisons of quantities
[E5].
Place the Scoop and Group Master and a container of
counters and a scoop in a learning center for students who
need additional practice with grouping, counting, and
representing larger quantities.


















 100 + 30 + 8. How did you solve this
problem? (Possible response: I first decided to
check to see if the number sentence was equal to
138 and it is.)
100 + 30 + 8. How did you solve this
problem? (Possible response: I first decided to
check to see if the number sentence was equal to
138 and it is.)