Button Solutions

Est. Class Sessions: 2

Developing the Lesson

Show $1 in Different Ways. Begin the lesson by reviewing the ways students learned in first grade to make $1.00 using nickels, dimes, and quarters. Ask students to work with their partner to come up with two ways to make $1.00. After students have had a few minutes, ask them to use a display set of coins to share their solutions as you record them on the chart. See Figure 1. Encourage students to count the coins to show how they make $1.00.

Share Strategies and Tools. Next have students look at the card samples on the Bertha’s Button Boutique pages in the Student Activity Book.

Pose the following problem:

Maya was sent to the Button Boutique to buy two buttons for a coat. Maya decided that the button on Card C was the best for her mother’s coat. How much will two buttons cost?

Ask students to consider how they can solve this problem. As students give their ideas, list their strategies and tools on the board, accompanied by the students’ names. After a student has suggested a strategy, ask others to explain it in their own words or to solve a different but similar problem using the same strategy. See the Sample Dialog.

In the Sample Dialog, the teacher leads a discussion in which various solution strategies for Maya’s problem are suggested by students then explained by another in his or her own words.

Linda: I thought about money. I know that 25 cents is a quarter and I know that 2 quarters makes 50 cents, so I knew the answer is 50 cents.

Teacher: Good, Linda. Did anyone else solve it Linda’s way? Sandra?

Sandra: I did, too. My mom gives me 25 cents for sweeping the back porch, so if I do it 2 days in a row, I know I get 50 cents.

Teacher: Does thinking about a problem in terms of money help? Why do you think that is so?

Michael: Because we like money.

Nicholas: And we have to use it every time we want to buy something.

Teacher: That’s true. When we want to solve a math problem, it helps if we can connect it to something that we know really well, like money. So that’s Linda and Sandra’s strategy—thinking about money. [Writes it on the board.] Did anyone solve the problem in a different way?

Tanya: I used the number line. And I skip counted.

Teacher: Can you show us how, Tanya? [Hands Tanya the pointer for the class number line.]

Tanya: I know that when I skip count by 5s, I’ll land on 25. 5, 10, 15, 20, 25. So that’s my first 25 and that’s where I start.

Teacher: Then what did you do?

Tanya: I do it 5 times more because that will get me another 25. So I start and say 25. Then I go 30, 35, 40, 45, 50.

Roberto: I just skip counted by 5s on my fingers and didn’t do the number line. I still got the same answer.

Teacher: That’s fine, Roberto. Let’s write that as a different strategy, though. We’ll call it Roberto’s strategy, skip counting by 5s with fingers. And we’ll call Tanya’s strategy skip counting by 5s on the number line. Anyone else?

Jessie: We used to do lots of things with ten frames, so I always think about how it looks in a ten frame.

Teacher: How do the ten frames help you with this problem, Jessie?

Jessie: I picture that 25 has 2 tens in it because of the 2. So that is 2 whole ten frames and 5 left over. So if I add 25 again, now that’s 4 whole ten frames and another 5 left over. Two 5s make a ten, so now that’s another full ten frame. Now it’s 5 full ones in all. And that’s 50. 10, 20, 30, 40, 50.

Teacher: Very good, Jessie. That’s a lot to picture in your head, but I can see how it helps you solve this problem. Who would like to describe Jessie’s strategy for us? Use your own words. You may use the ten frames if you like.

Tell students to work in pairs to solve the problems on the Bertha’s Button Boutique pages in the Student Activity Book. Display and ask students to turn to the Math Practices page in the Reference section of the Student Activity Book.

As students share their solution to the problems, reference the appropriate Math Practices expectations and ask:

How did you decide what the problem is about? (Possible responses: I acted it out; I used connecting cubes to show the parts of the problem.)
What tools did you use to solve the problem? (Possible response: number line, cubes)
What number sentence shows how you solved the problem?
Is there another tool that would also show your strategy?
What did you write down to show how you solved the problem?
Who can tell us how [student name] solved this problem?

The Math Practices page sets expectations for solving problems and communicating solution strategies. By regularly revisiting and monitoring these expectations, students can internalize these habits of mind and learn how to clearly show their solution paths. Feedback Boxes help communicate expectations and criteria for knowing how those expectations are being met.

Discuss Math Practices Expectations. Distribute and read the problem on the Button Collection Master. Ask students to solve the problem.

Ask:

While you were solving this problem, which of the Math Practices did you use? (all of them)
Why? (Because while solving a problem you need to do all of these things. You need to understand the problem, choose a good strategy, etc.)

Tell students to look at their work and ask:

Do you think you showed your work so someone else can tell how you arrived at your answer?
Did you label the numbers and steps in your problem?

Next ask students to look at their neighbor’s work and ask:

Can you tell how your neighbor solved the problem?
Did they label their work?

Display the Jackie’s Work Master and ask:

How did Jackie solve the problem? (not sure)
Did she show how she solved the problem? (No, she did not.)
Did she show anything that helps us figure out what she was thinking? (no)
What should we tell Jackie about showing her work? (Possible responses: Tell her that she did not show her work.)
Did Jackie use any labels? (no)
What would you tell her? (Possible response: I would remind her to label her work.)

Use the Feedback Box at the bottom of the Jackie’s Work Master to provide her with feedback about Math Practice Expectations 5 and 6. Both sets of feedback would be under the “No” column of the feedback box. See Figure 2.

Display the Jerome’s Work Master and ask:

How did Jerome solve the problem? (Possible response: He drew a picture of 22 buttons and then took away 10 buttons and 8 buttons.)
Is there anything you do not understand? (Possible response: I am not sure how he subtracted. Did he think 22 and then 12 to subtract 10, or did he count back?)
Did he show his work? (Possible responses: Yes, he did; or Yes, he did, but he did not show his strategy.)
Look at the feedback box. What feedback would you give him? (Possible responses: Yes, he showed how he subtracted; or Yes, but his strategy for subtracting could be clearer.)

To help students decide on the types of feedback the student needs, describe the column headings of the feedback box:

“Yes . . .” indicates that the Math Practice was carried out completely and clearly.
“Yes, but . . .” indicates that the Math Practice was carried out well but with a minor error or omission, or could possibly have an incorrect answer but shows use of a good strategy.
“No, but . . .” indicates that there was a good attempt to carry out the Math Practice, but there is a major error or omission.
“No . . .” indicates that the Math Practice was carried out with many errors or is not present.

Complete Jerome’s Feedback Box. See Figure 3.

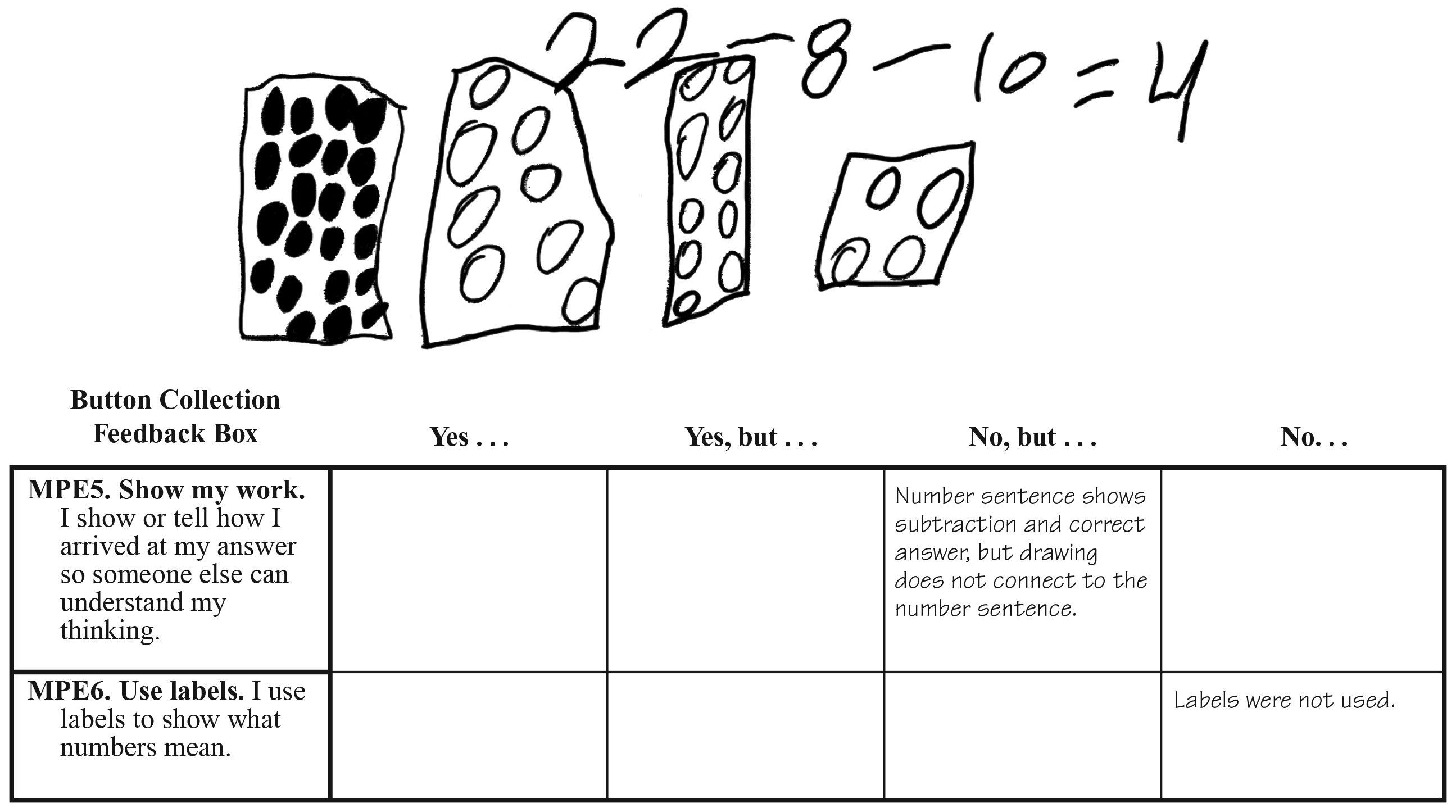
Though the expectations outlined on the Math Practices page are universal to problem solving, some are more difficult to observe in some problem situations. You can choose to focus on only those expectations that seem appropriate to the particular problem or that meet the needs of your students. As students gain experience with the expectations and criteria outlined, they will become more comfortable applying it to their work and to the work of other students.

Use a similar process with the Grace’s Work Master asking the same or similar questions. Grace’s answer uses the minus sign in her number sentence, but her drawing does not indicate how or what she subtracted or “took away.” Complete the feedback box for Grace’s work together. See Figure 4.

Ask students to look at their own solution to the problem on the Button Collection page.

Ask:

Did you show all your work?
Did you use labels to show what your numbers mean?

Encourage students to revise their work to meet the Math Practices Expectations.

Practice Showing Math Practices 5 and 6. Tell students that they are to complete the Button Solutions pages in the Student Activity Book. Tell them they should think about Math Practice 5, Show my work, showing all their thinking and steps taken, and Math Practice 6, Use labels, in the steps in their solution and in their answer. As students are working, circulate asking students to clarify their written solutions and include labels on their work.

Use the Button Solutions page with the Feedback Box to assess students’ abilities to show their work [MPE5] and use labels [MP6].

At this point in 2^nd grade, students are using a variety of tools and strategies as they develop increasingly efficient strategies for adding and subtracting. It is important that students share these strategies and representations. How these tools (for example, drawings) relate to the number sentence is important in order to understand the strategies that students are using. See the examples of Jerome’s and Grace’s work. As students become less dependent on these tools, it will be less important for them to represent them in their solutions.

Adventure Book: