Strategies
“Knowing basic number combinations—the single-digit addition and multiplication pairs, and their counterparts for subtraction and division—is essential. Equally essential is computational fluency—having and using efficient and accurate methods for computing. Fluency might be manifested in using a combination of mental strategies and jottings on paper or using an algorithm with paper and pencil, particularly when the numbers are large, to produce accurate results quickly. Regardless of the particular method used, students should be able to explain their method, understand that many methods exist, and see the usefulness of methods that are efficient, accurate, and general.”
National Council of Teachers of Mathematics, Principles and Standards for School Mathematics, p. 32, 2000.
SUBTRACTION FACTS STRATEGIES

“Encouraging children to use efficient strategies to derive unknown facts before drill is better… read more
“Encouraging children to use efficient strategies to derive unknown facts before drill is better than 'premature drill'… and doing so increases both initial learning and retention” (Thornton, Mathematics for the Young Child, p. 134, 1990).
There is a body of research that supports students working toward math facts fluency in this manner. Generally, students move through three developmental stages when acquiring operational understanding and fluency with the math facts.
- Direct modeling in which students re-create the action in the problem using manipulatives;
- Counting strategies such as counting on and counting back; and
- Reasoning from known facts in which students work from facts they already know. For example, if a student knows that 13 − 10 = 3, then he or she has a quick way to access 13 − 9 (Carpenter, 1999, National Research Council, 2001).
Throughout the curriculum, students are encouraged to invent their own strategies and to share their thinking with one another. However, particular emphasis is given to the strategies described below.
Counting Strategies
Counting Up is most efficient when the numbers are close together, as in… read more
Counting Strategies
Counting Up is most efficient when the numbers are close together, as in 11 − 8 or 30 − 28. To subtract 8 from 11, students start at the lower number (8) and keep track of how many they count to get to 11 (9, 10, 11).
Counting Back is most efficient when the number to be subtracted is small, as in 11 − 3 or 30 − 2. In this case, students start at the higher number (11), count backward the amount of the lower number (3), and find the number they stop at (8).
Reasoning from Known Facts
Throughout second grade, students took part in lessons based on these stages that fostered… read more
Reasoning from Known Facts
Throughout second grade, students took part in lessons based on these stages that fostered the development of meaningful and efficient strategies. In this unit, students review strategies for addition and subtraction. While students should choose strategies that make sense to them, it is important to encourage them to develop flexible strategies in which they reason from known facts. These strategies are important because they can be used to efficiently find answers to single-digit fact problems and they can also be applied to problems with larger numbers.
Using Doubles. If students are comfortable with doubles, e.g., 8 + 8 = 16 and 6 + 6 = 12, they can use these facts to learn “half-doubles” as well: 16 − 8 = 8 and 12 − 6 = 6. These facts can then be used to figure out close facts, such as 13 − 6 = 7 and 15 − 8 = 7.
Making Tens. Students are often comfortable with sums of ten, e.g., 6 + 4 = 10, and can use them to find differences from ten, e.g., 10 − 6 = 4 and 10 − 4 = 6. Students used ten frames to visualize these problems in Grades K–2, as shown in Figure 1. These facts can then be used to find close facts, such as 11 − 4 = 7.
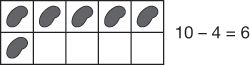
Figure 1: Using a ten frame to visualize 10 − 4 = 6
Using Tens. Students follow the pattern they find when subtracting ten, e.g., 17 − 10 = 7 and 13 − 10 = 3, to learn “close facts,” e.g., 17 − 9 = 8 and 13 − 9 = 4. Since 17 − 9 will be one more than 17 − 10, they can reason that the answer will be 7 + 1, or 8.
Thinking Addition. To find the answer to 15 − 8, a student thinks, “8 plus what number equals 15? Since 8 + 7 = 15, 15 − 8 = 7.”
MATH FACTS and MENTAL MATH

The goal of the math facts development in Math Trailblazers is for students… read more
The goal of the math facts development in Math Trailblazers is for students to learn the basic facts efficiently, gain fluency with their use, and retain that fluency over time. A large body of research supports an approach in which students develop strategies for figuring out the facts rather than relying on rote memorization. This not only leads to more effective learning and better retention, but also to the development of mental math skills. In fact, too much drill before conceptual understanding may interfere with a child's ability to understand concepts at a later date.
The research that contributed to the National Council of Teachers of Mathematics Principles and Standards for School Mathematics and the National Research Council's Adding It Up has informed the structure of the math facts strand in Math Trailblazers. Also see the Letter Home for more about the development of the basic facts in 3rd-grade Math Trailblazers.
Subtraction Facts. This unit begins a systematic review and assessment of the subtraction facts to maintain and increase proficiency and to learn to apply subtraction strategies to larger numbers. Students study small groups of facts that can be solved using similar strategies. See Figure 2.
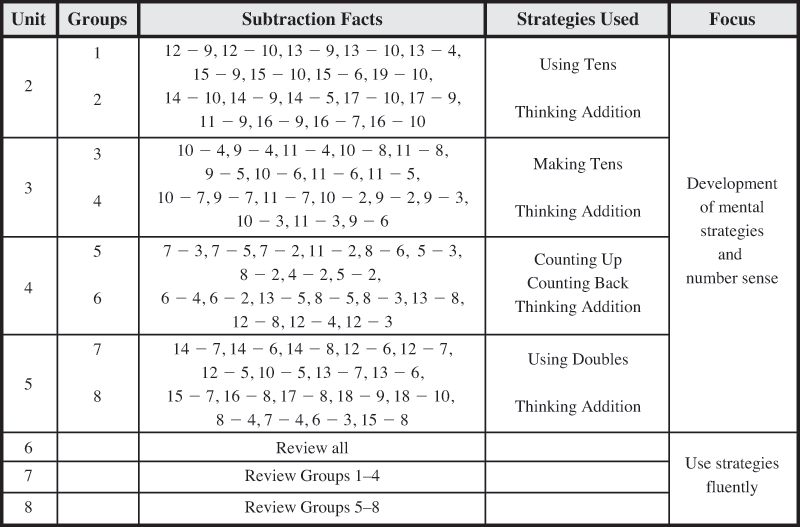
Figure 2: Development of subtraction facts in Grade 3
ALGEBRA in the EARLY YEARS

“The underlying goal of early algebra is for children to learn, see, and express… read more
“The underlying goal of early algebra is for children to learn, see, and express generality in mathematics” (Kaput, et al., 2008). Algebraic thinking can be the thread that connects mathematical experiences across and within grade levels. Proponents of algebra in the early grades argue that children are able to think about the structure and relationships of quantities and mathematics.
Algebra and Arithmetic. Arithmetic is often seen as a series of procedures to get to a particular correct result. This shortchanges the powers of a student's ability to form generalizations. Students need to use this power by inventing strategies, using multiple strategies, communicating their solution paths, and describing those generalized patterns. From those generalized patterns, young children can start to think about the specific properties of operations.
“In order to do arithmetic you already need to do algebra!” (Hewitt, 1998, pg. 19)
Equal Sign. At times, children view the two sides of the equal sign as a request to carry out an operation rather than a relationship between quantities. To broaden this view of the equal sign, equations are written in multiple ways and always to represent a relationship.
Resources
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH, 1999.
- Dacey, L. & Bamford Lynch, J. Math for All: Differentiating Instruction, Grades 3–5. Math Solutions Publications, Sausalito, CA, 2007.
- Hewitt, D. “Approaching arithmetic algebraically.” Mathematics Teaching, 163. The Association of Teachers of Mathematics, Derby, UK, 1998.
- Kaput, J., D. Carraher, and M. Blanton, eds. Algebra in the Early Grades. Lawrence Erlbaum: Taylor & Francis Group, New York, 2008.
- Mathematical Sciences Education Board. Measuring Up: Prototypes for Mathematics Assessment. National Academy Press, Washington, DC, 1993.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Payne, J.N., ed. Mathematics for the Young Child. The National Council of Teachers of Mathematics, Reston, VA, 1990.
- Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- Stenmark, J.K., ed. Mathematics Assessment: Myths, Models, Good Questions, and Practical Suggestions. The National Council of Teachers of Mathematics, Reston, VA, 1992.
- Thornton, C.A. “Strategies for the Basic Facts.” In J.N. Payne, ed. Mathematics for the Young Child. The National Council of Teachers of Mathematics, Reston, VA, 1990.
- Van de Walle, J. A., K. S. Karp, and J. M. Bay-Williams. Elementary and Middle School Mathematics: Teaching Developmentally, 7th. Ed. Pearson: Allyn & Bacon, Boston, 2010.
- Webb, N.L. & A.F. Coxford, eds. Assessment in the Mathematics Classroom. The National Council of Teachers of Mathematics, Reston, VA, 1993.











