Addition with Larger Numbers

Est. Class Sessions: 4

Developing the Lesson

Part 3: Review Two Paper-and-Pencil Addition Methods

All-Partials Method. This part of the lesson reviews and extends the two paper-and-pencil algorithms students learned in Lesson 4 to adding three- and four-digit numbers. Each method depends on place value and parallels a solution with base-ten pieces.

Explain that when people add, they usually do not have base-ten pieces around. Base-ten shorthand is always available to represent the pieces, but it is tedious. Remind students that we want to use efficient methods for adding. Refer students to the Addition Strategies Menu in the Student Guide Reference section. See Figure 3.

Display the problem 202 + 178 and ask:

Which strategy would you use to solve this problem? Explain. (Possible response: I can use mental math. I take 2 from 202 and add it to 178. Now it's 200 + 180 = 380.)
Who can solve this problem another way? (Possible response: I use base-ten pieces. 2 flats + 1 flat is 3 flats. 7 skinnies + 0 skinnies is 7 skinnies. 2 bits + 8 bits is 10 bits. I trade the 10 bits for another skinny, so now there are 8 skinnies and 0 bits. The answer is 380.)

Ask students to recall the opening problem, 678 + 267, in the Addition with Larger Numbers pages in the Student Guide. Nikia solved the problem as shown in Figure 8. Previously, students solved this problem by trading the base-ten pieces. Another way is to add up the value of the pieces without regrouping: 800 + 130 + 15 = 945. The first method, all-partials, is an algorithm based on this solution. With this method, you write the value of each piece under the problem.

Direct students' attention to the Paper-and-Pencil Addition Methods section and read the All-Partials Method section together as a class. Note that neither the order in which you add the columns nor the lines on which you write the corresponding sums matters. You can work from right to left or from left to right. Both ways are shown in the Student Guide. Discuss Question 2 to make connections between the notation and the value of the base-ten pieces.

Next, display the problem 197 + 534. See Figure 9.

Say:

Think about base-ten pieces to help you estimate. Does thinking about the number of flats or the number of bits help you to better estimate the sum? Explain. (Flats; Possible response: 197 is almost 200 or 2 flats. 534 has 5 flats. 2 flats + 5 flats is 7 flats, 7 hundreds, or 700. I estimate the sum to be around 700.)

Remind students that when they added with base-ten pieces, the order in which they combined the pieces did not matter. When estimating, however, combining the largest pieces makes the most sense. When using all-partials to find an exact sum, adding from right to left or from left to right does not matter. But to estimate a sum, if you begin on the left you only need to add one or two columns to estimate the size of the final answer.

Ask students to solve 197 + 534 using the All-Partials Method.

Then ask questions that help students make connections between the base-ten pieces and the places of the digits:

Why did you write 600? What did you add? (Possible response: I added 100 + 500.)
What base-ten pieces could you use to represent that number? (6 flats)
Why did you write 120? (Possible response: I added 90 + 30.)
What base-ten pieces did you think of when you added those numbers? (9 skinnies and 3 skinnies)
What base-ten pieces do you think of when you see the 11? (11 bits)
Think about base-ten pieces again. Using this method, does it matter what order you add the flats, skinnies, and bits? (No. You could add the bits together first, then add all the skinnies and flats together.)

Compact Method. The compact method is the algorithm traditionally taught in the United States. It requires less recording and therefore is more efficient for most students. Some students may find it more difficult because they have to make trades as they go along. Still others may have trouble learning this method because working left to right is more natural for them, perhaps because we read from left to right. The algorithm will work from left to right, but is not efficient—it would require crossing out and rewriting digits in the answer when regrouping.

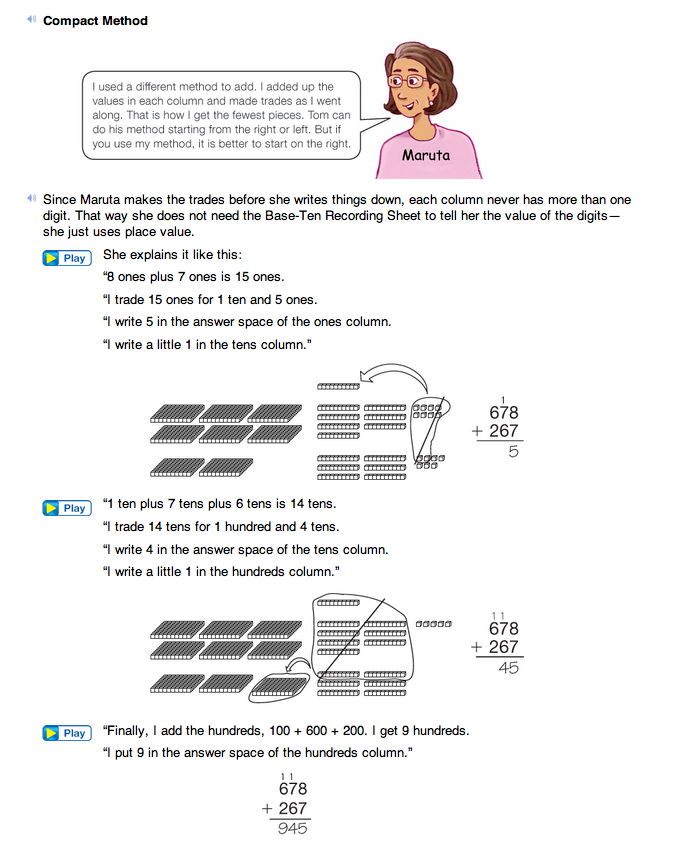
Compact Method. Distribute base-ten pieces to student pairs. Display the problem 678 + 267 once again. See Figure 10. Earlier in this section, students solved this problem by trading, and some probably traded from left to right while others might have traded from right to left.

Now ask:

Redo the problem with base-ten pieces, this time trading only from right to left, that is, from the smallest to largest pieces.

Ask students to combine the bits and make the trades. Record that answer in the space of the ones column for all to see. As students combine the skinnies and make trades, record that answer in the space of the tens column. Finally, record the number of flats in the space of the hundreds column. Show students that when done in this order, they can write down the digits of the answer one-by-one as they go along. Tell students the compact method is a paper-and-pencil method that records adding and regrouping from right to left as you go along.

Direct students' attention to the Student Guide pages and read the Compact Method section together as a class. Maruta shows how she solves 678 + 267 using the compact method.

Ask students to solve a few more problems using the compact method. As students solve the problems, help them to make connections between their paper-and-pencil solutions, the value of the places, and the base-ten pieces. Remind them to check the reasonableness of their answers. For example, have students solve 259 + 476. See Figure 11.

Ask:

Why did you write the little 1 above the 2? What did you add? (Possible response: I added the tens. 5 tens plus 7 tens plus the one ten from the bits is 13 tens. You can't write 13 in the tens column, so I put the 1 in the next column.)
What does the 1 above the 2 stand for? (one hundred)
What does the 3 in the answer stand for? (3 tens or 30)
How is what you did like using the base-ten pieces? (It's like adding skinnies and trading 10 of them to get a flat and having 3 skinnies left over.)
How did you decide your answer was reasonable? (Possible response: I thought of friendly numbers. Instead of 259, I thought of 250. Instead of 476, I thought of 500. 250 + 500 = 750. An answer of 735 is reasonable.)

Assign Questions 3–11 in the Student Guide.

As students work, ask questions such as the following:

What is the value of the number in the ones place? Tens place? Hundreds place?
How did you get this number?
Did you have to make any trades?
What base-ten pieces could you use to explain how you got this number in your answer?

Use Check-In: Questions 6–11 in the Student Guide and the corresponding Feedback Box Master to assess students' abilities to use place value concepts [E1]; add multidigit numbers using mental math [E3] and paper-and-pencil strategies [E4]; and to show estimation strategies to determine the reasonableness of solutions [E5], [MPE3], [MPE5].

Use the workshop in Lesson 6 to provide targeted practice on these expectations.

Assign the Homework section of the Addition with Larger Numbers pages in the Student Guide for additional practice with using the all-partials and compact methods.