MEASUREMENT CONCEPTS

Measure with Standard and Nonstandard Units
Throughout this unit, students explore measurement concepts using a variety … read more
Measure with Standard and Nonstandard Units
Throughout this unit, students explore measurement concepts using a variety of units of length. They estimate, discuss, predict, and share their observations and thinking. Students have a rich informal background with measurement. In Grade 1, they measured using nonstandard units (links, paper clips, feet). This unit builds on students' knowledge of nonstandard units and utilizes that experience to discuss the need for and importance of standard units. By measuring various objects with nonstandard units (such as palms and footprints) and standard units (inches, feet, yards, centimeters, and meters), students begin to develop an intuitive sense of the sizes of these measures.
When you measure the length of an object (or distance), you are comparing that distance to the length of a unit. Students need to grapple with a number of concepts to do this. Students start by working with nonstandard units to help develop a set of measurement techniques and unit comparisons. The nonstandard units help students grapple with how to work with discrete units and compare units of different sizes. Nonstandard units also present opportunities to talk about comparing the attribute of the length and how that compares to the length of the unit. Most standard units are lined up nicely on a ruler or tool and therefore do not create opportunities for students to think about how to line up the units without gaps or overlaps or even that the length of the unit and the length of the distance need to match. Nonstandard units also provide the opportunity to compare unit sizes that are very different without preconceived notions. The nonstandard units also create the need for standard units. Students will explore this idea of a standard unit in Lesson 5. They will collect data to decide how to choose a standard size for a palm unit. Most of our standard units are selected using a similar process.
Students then transition to standard units of length: centimeters, inches, feet, meters, and yards and explore the relative size of different units. They start by using physical models of these different units and compare them to the lengths they wish to measure. Then they use these experiences to decide if a measurement "could be" or is "crazy." These decisions help students consider the relationships between units and compare their relative size.
Students will be working with both U.S. customary and metric systems of measurement. Most scientific work is done using metric units but many distances are still measured with U.S. customary units. The goal is for students to be "bilingual" in measurement, able to use both systems confidently.
Estimate Length
Asking students to estimate helps students focus on the relative size of a … read more
Estimate Length
Asking students to estimate helps students focus on the relative size of a unit and how that unit relates to the attribute being measured. There are several strategies one might use to estimate:
- Develop or use a benchmark. Example: "I picture about the length of the 12-inch ruler. The object looks like it is less than the 12-inch ruler, but more than half of it. So I estimate about 10 inches."
- Iterate a unit mentally or physically. Example: "I pictured a yardstick and looked at the line. I pictured the yardstick would fit on the line about 4 times. So I estimate four yards."
- Use "chunking" when appropriate. Example: "I picture measuring parts of the hallway length, instead of the whole thing. I estimate the lockers to be about 8 metersticks and the door about 1 meterstick, so all together about 9 metersticks, or 9 meters."
- Use subdivisions. This can be closely related to "chunking." It may help to look at a length and mentally cut it in half (or a third, fourth, etc.) of its length. Example: "Line A is about half of line C. I know line A was 3 meters, so I estimate Line C to be 6 meters."
Students' abilities to estimate will improve with experience. Accept a wide range of estimates during your discussions. Encourage students to think about the relative size of a unit. Avoid promoting "winners" with the best estimates, as this can discourage students. Promote the usefulness of various strategies, as there is no one "right" method to estimate (Van De Walle, 2013).
TIMS LABORATORY METHOD

Compare and Use Measurements
The Rolling Along in Centimeters lab provides students with authentic reasons … read more
Compare and Use Measurements
The Rolling Along in Centimeters lab provides students with authentic reasons to measure and compare quantities. They collect data in order to compare measurements, determining which car is the "better roller." See Figure 1.
The type of car and the distance each travels are the two experimental variables that students study. This lab contains two basic ingredients of real-world experiments: (1) reliable results depend on doing everything the same way each time we complete a trial—in this case, rolling the cars, and (2) the results may not be the same each time (but they should be close). Experimental variables that stay the same are called controlled or fixed variables. Students understand controlled variables as keeping everything "fair."
Students will find that, despite keeping certain variables controlled, results vary. The cars will not roll the same distance each time. Scientists conduct more than one trial for each observation; i.e., they perform the experiment several times to account for these discrepancies. Like scientists, students will conduct several trials, then use an average. One type of average is a median, or middle value. To find the median, students can roll a car down the ramp three times, mark the distance of each roll, and measure only the middle distance, or they can measure all three distances and use the value in the middle.
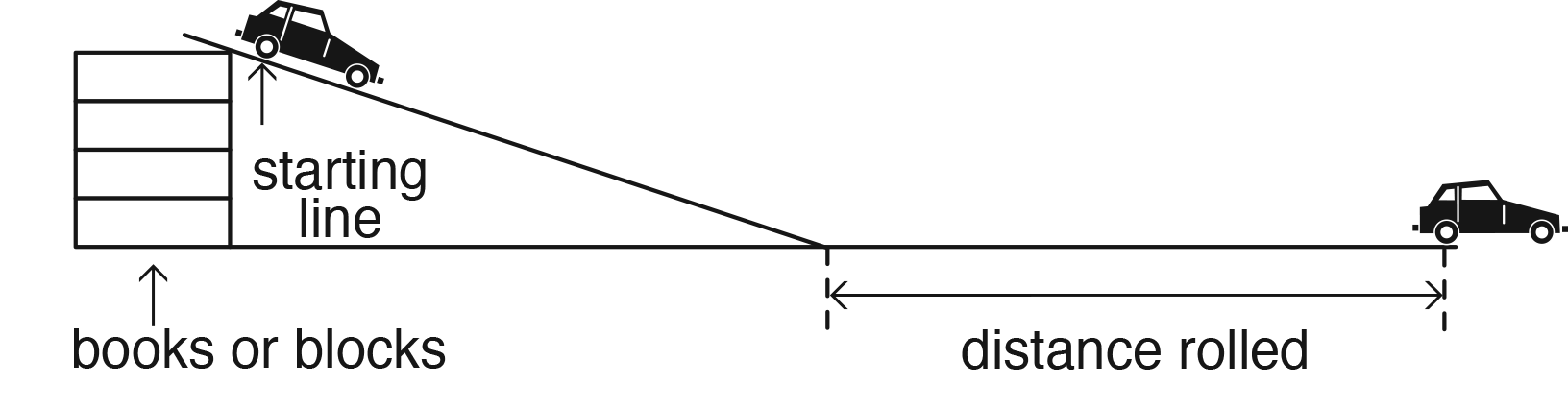
Figure 1: Measuring distance rolled
MATH FACTS and MENTAL MATH

Addition Facts
In this unit, students continue to systematically review the addition facts. Daily Practice and Problems … read more
In this unit, students continue to systematically review the addition facts. Daily Practice and Problems items in this unit can be used to assess students' strategies with the addition facts in Group E (5 + 7, 8 + 4, 8 + 5, 9 + 3, 9 + 4, 9 + 5, 10 + 1, 10 + 2, 10 + 3).
These facts involve the make-ten and use-ten addition strategies.
Making Ten
To solve 8 + 4 the 4 is split to make ten with the 8:
8 + 2 = 10, 10 + 2 = 12.
Using Ten
To solve 9 + 3, think 10 + 3 = 13, so 9 + 3 is one less
or 12.
As students develop fluency with these facts, they will be able to name the related facts in the fact family.
Resources
- Baroody, A.J. "Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them. "Teaching Children Mathematics, 13 (1), pp. 22–31, 2006.
- Brownell, W.A., and C.B. Chazal. "The Effects of Premature Drill in Third-Grade Arithmetic." Journal of Educational Research, 29 (1), 1935.
- Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically: Integrating Arithmetic & Algebra in Elementary School. Heinemann, Portsmouth, NH, 2003.
- Carpenter, T.P., E. Fennema, and P. Peterson. "Cognitively Guided Instruction: The Application of Cognitive and Instructional Science to Mathematics Curriculum Development." In Developments in School Mathematics Education around the World: Applications-Oriented Curricula and Technology-Supported Learning for All Students. I. Wirszup and R. Streit, eds. National Council of Teachers of Mathematics, Reston, VA, 1987.
- Carpenter, T.P., and J.M. Moser. "The Acquisition of Addition and Subtraction Concepts in Grades One through Three." In Journal for Research in Mathematics Education, 15 (3), 1984.
- Council of Chief State School Officers. Common Core State Standards for Mathematics, 2010.
- Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherance. The National Council of Teachers of Mathematics, Reston, VA, 2006.
- Hiebert, James. "Relationships between Research and the NCTM Standards." Journal for Research in Mathematics Education, 30 (1), pp. 3–19, 1999.
- National Research Council. "Developing Proficiency with Whole Numbers." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Research Council. "Teaching for Mathematical Proficiency." In Adding It Up: Helping Children Learn Mathematics, pp. 181–229. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Van De Walle, J.A., K.S. Karp, and J.M. Bay-Williams. Elementary and Middle School Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc., Upper Saddle River, NJ, 2013.












