Have students analyze and discuss their results.
Allow time for several students to share the data
they collected and to explain how they found the
volume of a set of objects. Ask students to compare
the measured volume of the train of centimeter connecting
cubes with its known volume. We will use a
train of 8 cubes as an example.
Pose the following
questions:
- Which object did you know the volume of ahead of
time? (the train of centimeter connecting cubes)
- What was its volume? (8 cc)
- What did you measure its volume to be in the
graduated cylinder? (Answers may vary. The volume
should be 8 cc.)
- What was the water level after you added the cube
train? (88 cc)
- How did you figure out the volume? (88 − 80 = 8 cc or 80 + 8 = 88 cc)
- You found the volume two ways: counting cubes
or replacing the object in the graduated cylinder.
Did the measurements match?
- I have another object. This object has a volume of
15 cc. What is the volume of the cube train and
this object together? (Possible response: 23 cc)
- What will happen to the water level if I place this
15 cc object and the cube train to the graduated
cylinder? (Possible response: The water will rise
to 103 cc; that is over 100 cc.)
Make sure students understand that the water level
rises because of the volume of the object, not the
mass of the object.
- How is this lab different from the lab
Marshmallows and Containers? (In the lab
Marshmallows and Containers, we found the
volume by measuring how much a container
could hold inside. This is also called the capacity,
or space inside a container. In this lab, we found
the space each object takes up.)
Explore the Volume Data. Ask student pairs to discuss
and complete Questions 4–10 in the Student
Activity Book.
While students are working, circulate
and ask:
- How did you solve that problem?
- What did you need to know to solve that problem?
- How did you compare those two volumes?
When most students have completed Questions
4–10, discuss Questions 9–10.

Use the Measuring Volume pages with the Feedback Box in
the Student Activity Book to assess students' abilities to use
words and symbols (e.g., <, >, =) to show comparisons of
quantities (e.g., volumes) [E1]; use and apply place value
concepts and comparative language to compare and order
volumes (e.g., most, least, greater) [E2]; solve addition and
subtraction problems (e.g., part-whole, join, compare)
involving volume [E3]; read and interpret a variety of scales
(e.g., graduated cylinder, thermometer) [E4]; measure
volume by displacement using a graduated cylinder [E5];
make a bar graph to find information about a data set [E6];
read a table and bar graph to find information about a data
set [E7]; and use a table and bar graph to solve problems
about a data set [E8].
To provide targeted practice with measuring volume by
displacement, place copies of the Measuring Volume Practice
Assessment Master and the necessary supplies in a learning
center. Students can measure volume to then compare and
order the volume of those objects.
In Question 9, students represent a problem using a
symbol for the unknown number.
Discuss solution
strategies and then discuss ways to represent the
problem with prompts similar to the following:
- What number sentence did you use? (Answers
will vary.)
- How does 50 cc + = 105 cc represent this
problem? (Possible response: It shows the numbers
and the missing number in the order the
information was told in the problem. It shows that
you join the 50 cc to the unknown number to get
105 cc.)
- What strategies would you use to solve
50 cc + = 105 cc? (Possible response: You
could add or subtract, or count up or down on a
number line.)
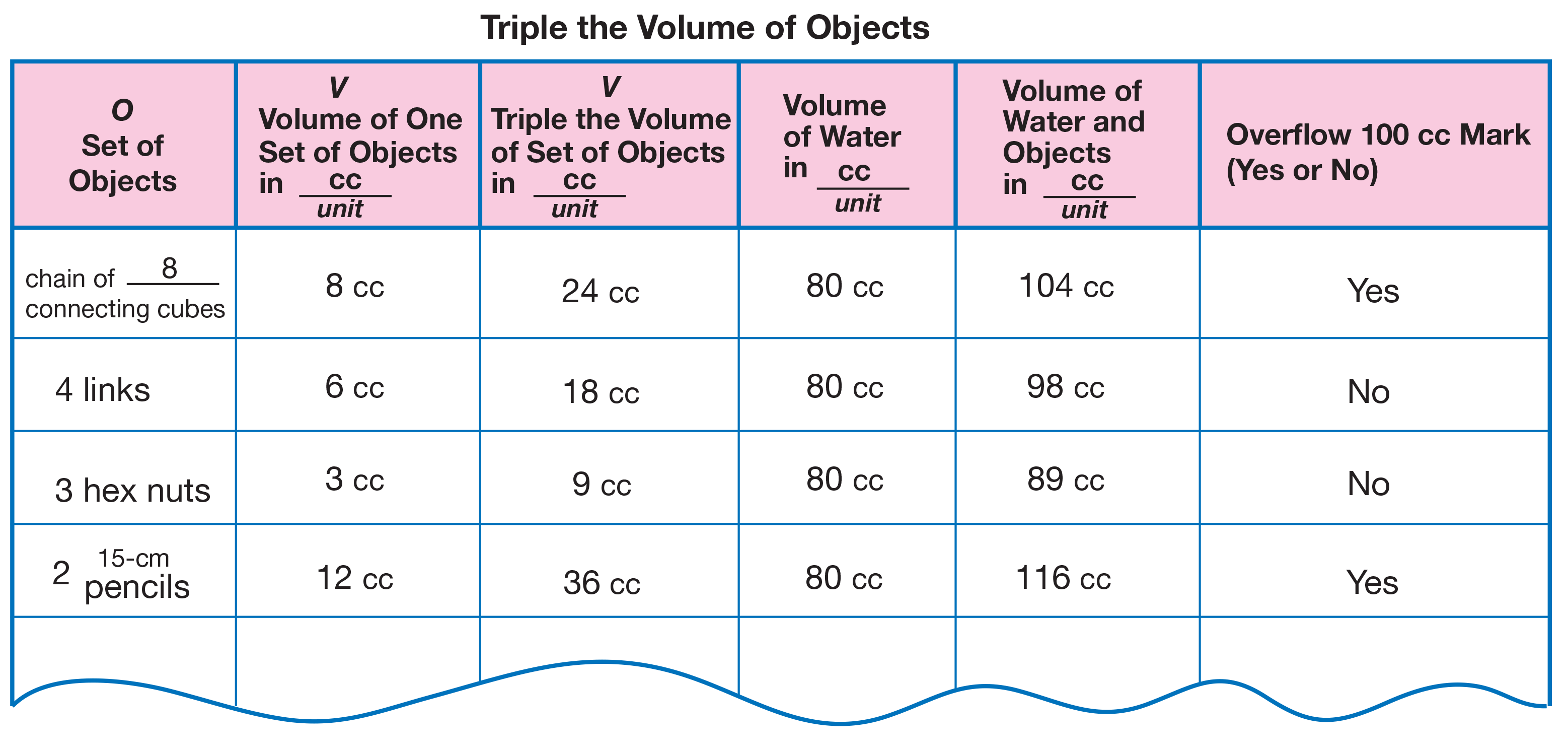
For Question 10, students find strategies to triple the
volume of an object and then determine if the water
will overflow the 100-cc mark on the graduated
cylinder. Have students read the problem.
- What do you need to determine first to answer the
questions? (You need to know how much the
water will rise when three rocks are added.)
- What do you think will happen? Share your prediction. (Possible responses: I think the water will go
up a lot and be close to 100 cc. I think the water
will go past 100 cc and will spill over the top.)
- When you add or skip count three times, you triple
the starting amount. What is triple the volume of
5 cc? How did you find out? (Possible responses:
Triple 5 cc is 15 cc. I added 5 three times to get
15 cc. I skip counted by five three times: 5, 10,
15 cc.)
See the Sample Dialog and Figure 5 for three different
students' strategies for tripling a quantity.

The following examples show different student approaches
to tripling a number. The examples are excerpted from a
videotape of a classroom discussion.
Teacher: How did you triple the amount of your volume?
And then tell how you decided whether it would
overflow the 100-cc mark?
Jacob: I did one pencil and when I put it in, it was 4 cc. So 3 times that is 12.
Teacher: How did you know 3 times 4 is 12?
Jacob: I knew that 3 times 4 would be 12 because I knew
that 4 plus 4 is 8. And 2, if you break 4 into 2 + 2, you
can put 2 to the 8 and then you'll have 10. Then you
add another 2 and that equals to 12.
Teacher: So does that make the water overflow the 100-cc
mark?
Jacob: No. See, you start at 80. You take 10 and that's 90.
Then 2 more is only 92.
Grace: I learned how to find 3 times, but I did it a different
way.
Teacher: How did you do it?
Grace: I did it by plusses.
Teacher: And how did you do that?
Grace: Like with my links, I had 4 links, and it was 8.
Teacher: Eight what, Grace?
Grace: 8 cc. 4 links is 8 cc. Eight plus 8 is 16, plus another 8
is 24.
Allow time for students to complete the problem and
ask them to describe what they thought would happen.
- How did you determine what will happen? How do
you know? (Possible response: It overflowed the
100-cc mark but there is enough room at the top
of the graduated cylinder so it doesn't spill over.
Possible responses: I skip counted by 20 cc three
times starting at 50 and ended at 110 cc: 50, 70,
90, 110. I added 20 three times:
20 + 20 + 20 = 60 cc and then added
60 + 50 = 110 cc.)