Find Volume Using Different Amounts of Water. Show students a graduated cylinder filled with 30 cc
of water and train of 20 centimeter connecting
cubes.
- I have 30 cc of water in this graduated cylinder. If I
add this train of 20 connecting cubes, what will the
total volume be? (Possible response: 50 cc)
- How did you figure that out? (Possible response: I
added the volume of the water to the volume of
connecting cubes.)
Show students a graduated cylinder filled with 75 cc
of water and the train of 20 centimeter connecting
cubes.
- I have 75 cc of water in this graduated cylinder. If I
add this train of 20 centimeter cubes, what will the
total volume be? (Possible response: 95 cc)
- How did you figure that out? (Possible response: I
added the volume of the water to the volume of
the connecting cubes.)
- What is different about these two problems? (Possible response: The volume of the water is
different.)
- What is the same about these two problems? (Possible response: The volume of the cubes is
the same.)
Now show students the graduated cylinder with
30 cc of water and a small object with a volume that
is about 20 cc.
Place the object in the graduated
cylinder and ask:
- What is the volume of the water and the small
object? (Possible response: 48 cc)
- What is the volume of the object? (Possible
response: [48 cc] − 30 cc = [18 cc])
Show students the graduated cylinder with 75 cc of
water and ask:
- If I move the small object to this cylinder, what will
the total volume be? (75 cc + 18 cc = 93 cc)
- Did the volume of the small object change? (Possible response: No, the volume of the object
did not change.)
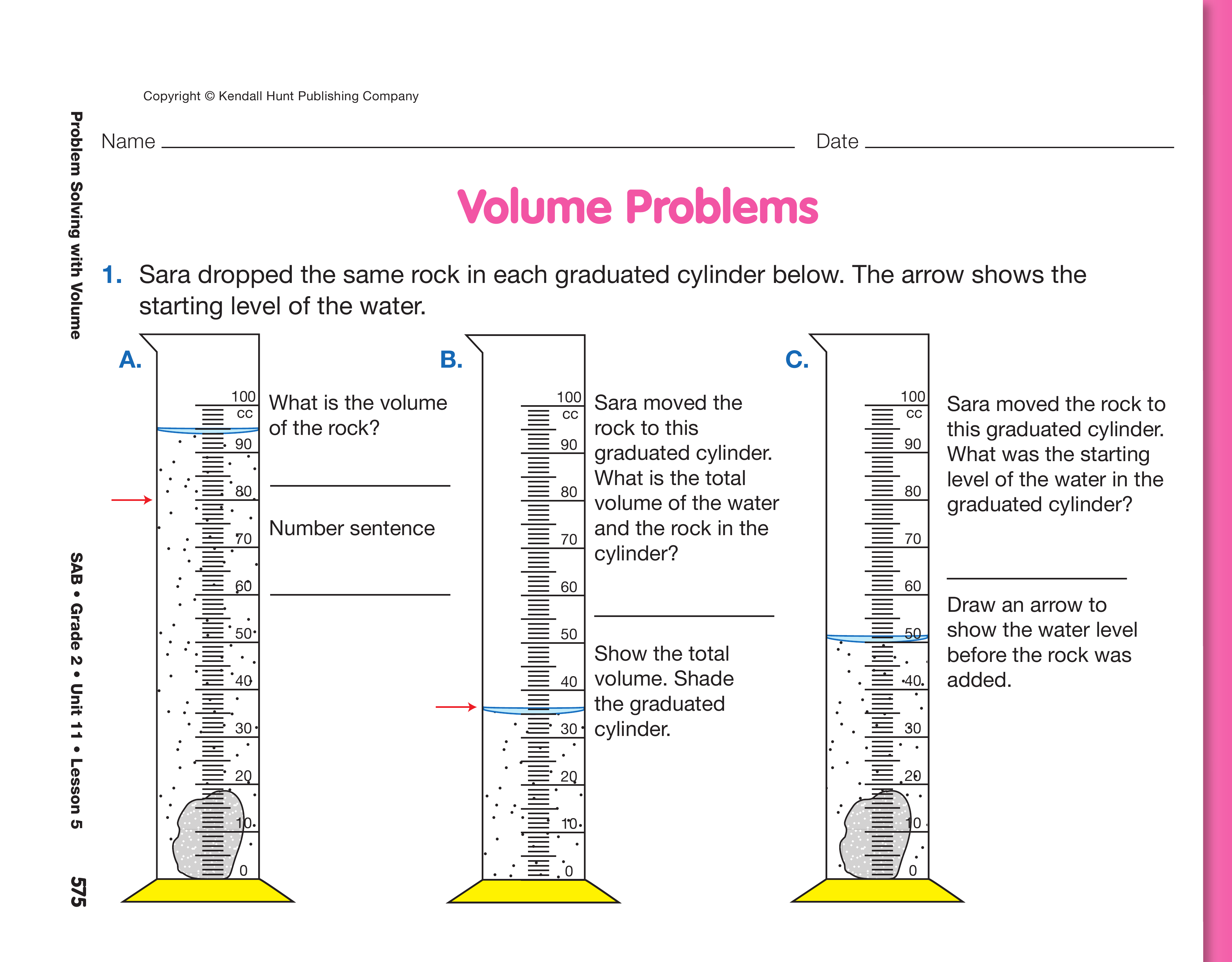
Next, ask students to discuss Question 1 on the
Volume Problems pages in the Student Activity Book
with a partner. Display a copy of the question and
remind students that the arrow next to each graduated
cylinder indicates the volume of water in the
graduated cylinder at the start.
After students have had a chance to work with their
neighbor, discuss strategies as a class.
Ask prompts
similar to the following:
- How did you find the volume of the rock in
Question 1A? (Possible response: I skip counted
by ten from 80 to 90 then by ones to 94 cc.)
- What is the volume of the water and the rock in the
graduated cylinder for Question 1B? What was
your strategy for finding the total volume of the
rock and the water in the graduated cylinder? (49 cc. Strategies will vary. Possible response: I
added 35 and 14 because 35 cc is the starting
level of the water in the graduated cylinder and
15 cc is the volume of the rock.)
- What number sentence represents your thinking? (35 cc + 14 cc = 49 cc)
- [Student name], will you shade the total volume of
the rock and the water on the display?
- What was the starting level of water in the graduated
cylinder for Question 1C? What was your
strategy for finding the starting volume of the
water in the graduated cylinder? (36 cc. Strategies
will vary. Possible response: I subtracted 14 from
50 because the ending water level of 50 cc shows
the total volume with the rock and the volume of
the rock is 14 so I took away 14 cc.)
- What number sentence represents your thinking? (Possible responses: 50 cc − 14 = 36 cc;
+ 14 cc = 50 cc)
- [Student name], will you draw an arrow to show
the starting volume of the water on the display?
Share Volume Problem Solution Strategies. Display and direct students' attention to Questions
2–3 on the Volume Problems pages in the Student
Activity Book and explain that in these problems the
starting level of the water in each graduated cylinder
is different. Have students work in pairs to find and
agree on a solution for each problem.
After adequate time has been provided, discuss solutions
to Question 2. Counting up and skip counting
by fives starting at 50 cc are effective strategies for
solving the problem, as well as counting the marks
on the cylinder.
Discuss students' strategies with
prompts similar to the following:
- What is the total volume of the rock and water in
the graduated cylinder? (75 cc)
- How did you know where to start counting to find
the total volume of the water and rock? (The problem
said John put 50 cc of water in the cylinder,
so that is the starting level of water, and then I
count up from there.)
- What number sentence represents this strategy for
finding the total volume? (50 cc + 25 cc = 75 cc)
- [Student name], come shade the total volume on
the display on Question 2.
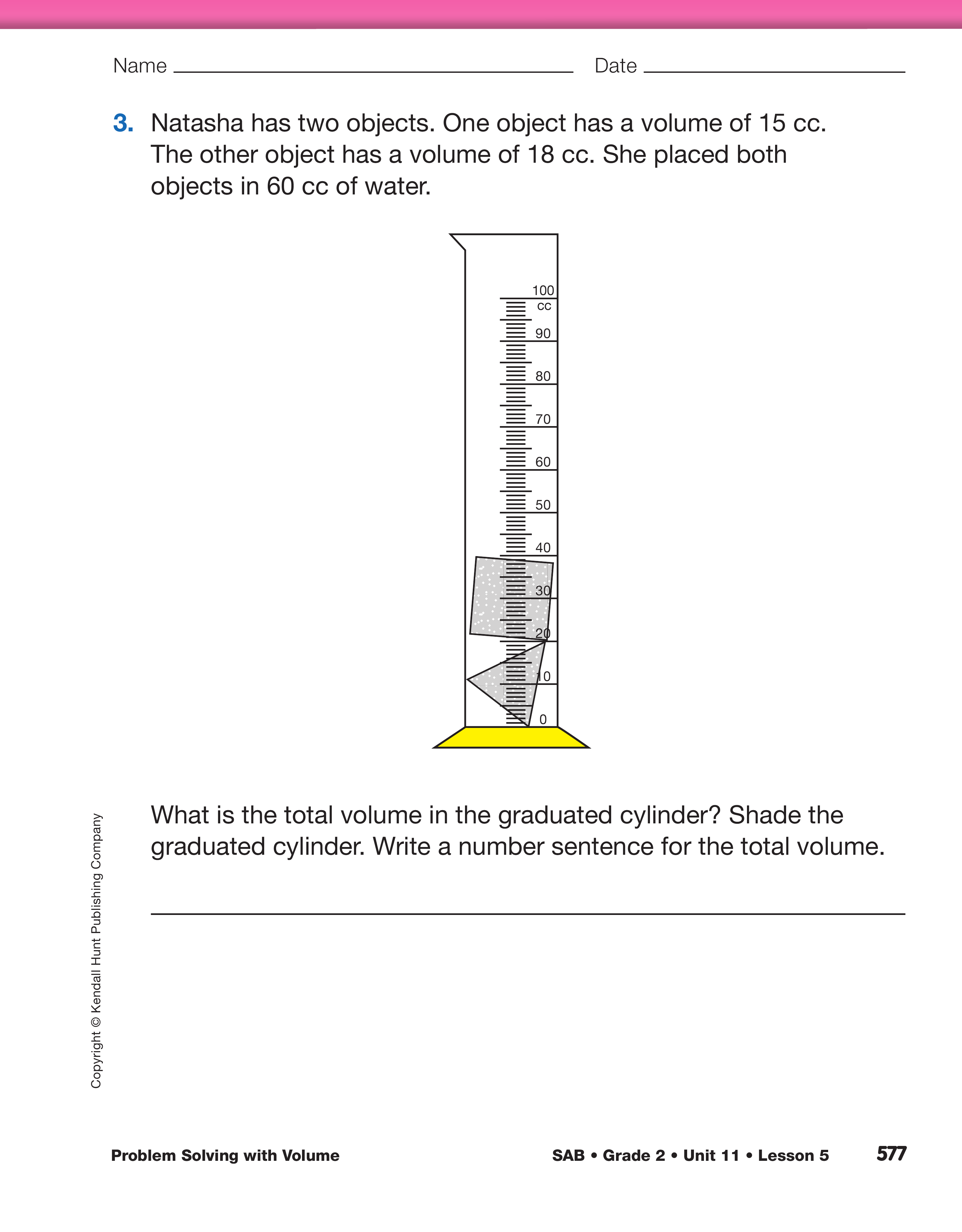
For Natasha's problem in Question 3, students
should note that determining the volume reading
involves a two-step process. In one solution, for
example, students first find the volume of Natasha's
two objects, and then add that number to the volume
of water. Or, they might add the objects' volumes to
the water one at a time. Encourage students to record
their number sentences as they explain their strategies
for finding the answer.
Use prompts similar to
the following to discuss solution strategies:
- What is the total volume of the objects and water
in the graduated cylinder? (93 cc)
- What did you need to do to solve this problem? (Possible response: I added the volume of the
two objects together first then counted up from
60 cc to find the total.)
- What number sentence represents your thinking? (15 cc + 18 cc = 33 cc and
33 cc + 60 cc = 93 cc)
- Did anyone use a different strategy? (Possible
response: I started at 60 cc and counted up 15 cc
for the volume of the first object, then counted up
18 cc more for the volume of the second object.)
- What number sentence represents your strategy? (60 cc + 15 cc = 75 cc and
75 cc + 18 cc = 93 cc)
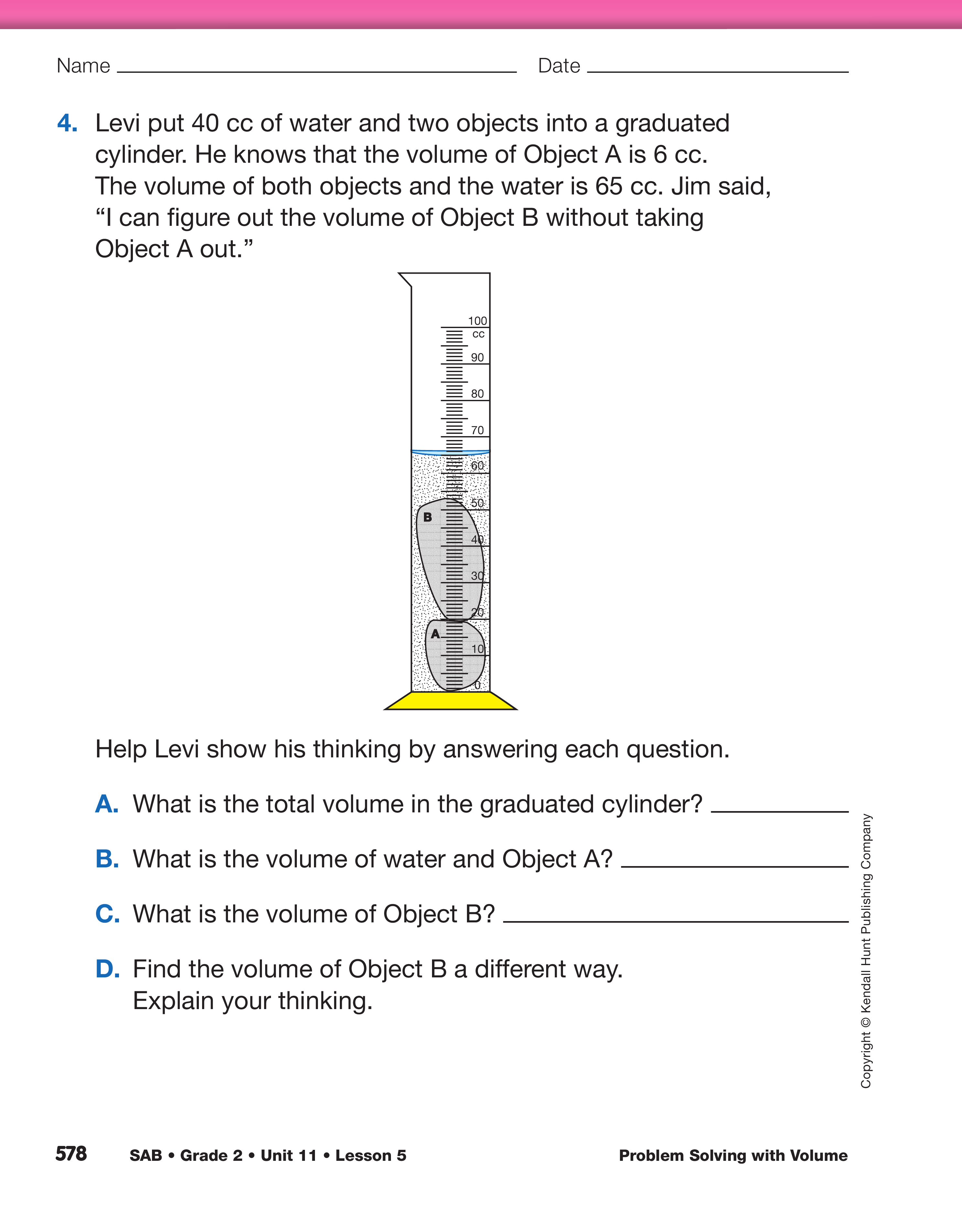
Next show a display of Question 4. Have students
read the problem then ask:
- What number sentence shows the known and
unknown information in the problem before solving? (40 cc + 6 cc + = 65 cc)
Have student pairs solve the problem, and allow
time for students to discuss their strategies and solution
paths with the class.
Conduct a discussion using
prompts similar to the following:
- What is the total volume of both objects and the
water in the graduated cylinder in Question 4A?
Why do you think Levi started with the total volume
in the graduated cylinder? (65 cc. He could
find that information easily by reading the meniscus
and use it to take away the other volumes he
knows to find out the unknown volume of the
second object.)
- How did you find the volume of water and Object A
for Question 4B? (Possible response: The problem
said Levi put 40 cc of water in the graduated
cylinder and he knew that the volume of Object A is 6 cc so I added 40 + 6 = 46 cc.)
- Why do you think Levi added the starting volume
of water to the volume of Object A? (Possible
response: Since he knows that information, he
can take it away from the total volume and find
the missing volume of Object B.)
- What is the volume of Object B? What number
sentence did Levi write using his known information? (65 cc − 46 cc = 19 cc)
- How did you solve the problem a different way in
Question 4D? Where did you start? What did you
do first? Explain your thinking. (Possible
response: I subtracted the volume of Object A
from the total volume in the graduated cylinder:
65 cc − 6 cc = 59 cc. That shows the volume of
Object B and the water together, so I subtracted
the starting volume of the water from that to get
the volume of Object B: 59 cc − 40 cc = 19 cc.)
- Did anyone solve the problem another way?
Explain your thinking. (Possible response: I subtracted
the starting volume of water from the
total volume in the graduated cylinder,
65 − 40 = 25 cc, then subtracted the volume of
Object A, 25 cc − 6 cc = 19 cc.)