Measuring Volume

Students studied the volume of containers in the Marshmallows and Containers lab in Unit 5 and investigated the volume of objects built out of cubes in Unit 10 Addition Properties Using Volume. In this unit, students measure the volume of objects using graduated cylinders. These activities provide an engaging context for practicing addition and subtraction skills.

To measure volume precisely, a unit of measure is needed. The metric unit of volume that we will use most often is the cubic centimeter (cc)—the volume of a cube that measures one centimeter on each side.

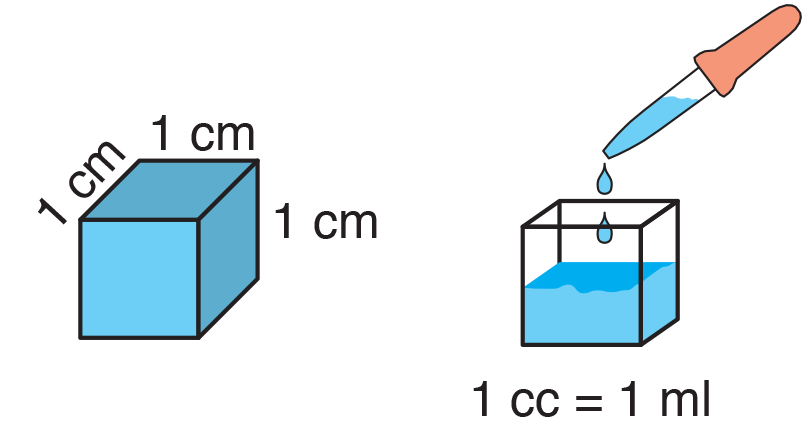
Figure 1: Metric unit of volume: 1 cubic cm (1 cc) = 1 milliliter (1 ml)

Finding the volume of an object built out of centimeter cubes is easy—just count the cubes. It is more difficult, however, to directly measure the volume of everyday objects. It would seem necessary to cut the object into cubes to find its volume. Fortunately, over 2000 years ago, the Greek scientist Archimedes discovered an ingenious way to find the volume of objects—immerse the object in water and then measure the volume of water that is displaced by the object.

In this unit, students fill a graduated cylinder with a specific amount of water and then submerge an object in the water. Students read the new level and use that reading and the initial reading to calculate the volume of the submerged object.

The graduated cylinder is an important tool for scientists. Just as metersticks provide a convenient way of measuring length, graduated cylinders provide an easy way of measuring volume.

Most graduated cylinders are calibrated in milliliters since milliliters are often used to measure the volume of liquids. A milliliter is equal to a cubic centimeter. See Figure 1. We prefer to use the term cubic centimeter because it reminds students of the meaning of the unit—a cube that is 1 cm on each side.

Since a graduated cylinder and many other scales can be calibrated in increments other than one, students need to learn how to interpret a variety of scales. However, students who are just beginning their work with graduated cylinders should use cylinders calibrated in increments of one. See Figure 2.

Figure 2: A graduated cylinder with every cubic centimeter indicated

In the first lesson, Reading Scales, students interpret scales of varying increments. Once students have mastered this skill, they need to learn how to read a graduated cylinder properly. In the second lesson, Reading Graduated Cylinders, student pairs record and discuss their readings of graduated cylinders. In the third lesson, Filling Graduated Cylinders, student pairs take turns filling and reading graduated cylinders.

The Measuring Volume lab provides an opportunity for students to use their knowledge of volume and graduated cylinders to measure the volume of several objects. It also provides a context for practicing addition and subtraction of two-digit numbers.

In the last lesson, Problem Solving with Volume, students continue to practice their computation skills by finding the answers to several questions involving volume. These questions engage students in different kinds of problem-solving situations. Many require multistep solution strategies.

We have found that as students use graduated cylinders, they develop strategies for working with numbers that are related to the interval structure on a scale, or number line. Thus, the graduated cylinder becomes a tool for measuring volume, visualizing the number system, and honing computation skills.

Multistep Problem Solving

Measuring volume by displacement and solving problems related to finding volume displacement creates an authentic and rigorous context to develop students' abilities to solve and maneuver multistep problem solving situations. Encourage students to act out the problem to help them choose an appropriate strategy.

"An important part of our conception of mathematical proficiency involves the ability to formulate and solve problems coming from daily life or other domains, including mathematics itself. The ability is not being developed well in U.S. pre-K to grade 8 classrooms. Studies in almost every domain of mathematics have demonstrated that problem solving provides an important context in which students can learn about number and other mathematical topics" (National Research Council, "Conclusions and Recommendations," 2001).