Lesson 3

Estimate Products

Est. Class Sessions: 3

Developing the Lesson

Part 2: Estimating a Range of Answers

Sometimes we only need to know a range within which the exact answer lies. We do not need to know the exact number. The two numbers at the low and high end of the range should give an idea of how big or small the answer is, depending on the problem.

In Questions 5A–C of the Student Guide, students are asked to estimate the range of the number of dead skin cells shed by all the students in the school each minute. Since this is an estimate there may be many answers to each part of this problem. As students share their responses, encourage them to explain their reasoning. For example, to find the range of possible answers for the number of skin cells shed by all the students in the school, we can first round 638 (the actual number of students) to a more convenient number. For the purpose of this problem we will use 600. To find the low end of the range we multiply 600 × 30,000 = 18,000,000. To find the high end of the range, we can multiply 600 × 40,000 = 24,000,000. Using this strategy, the range for the number of dead skin cells shed each minute by students at the school is between 18,000,000 and 24,000,000.

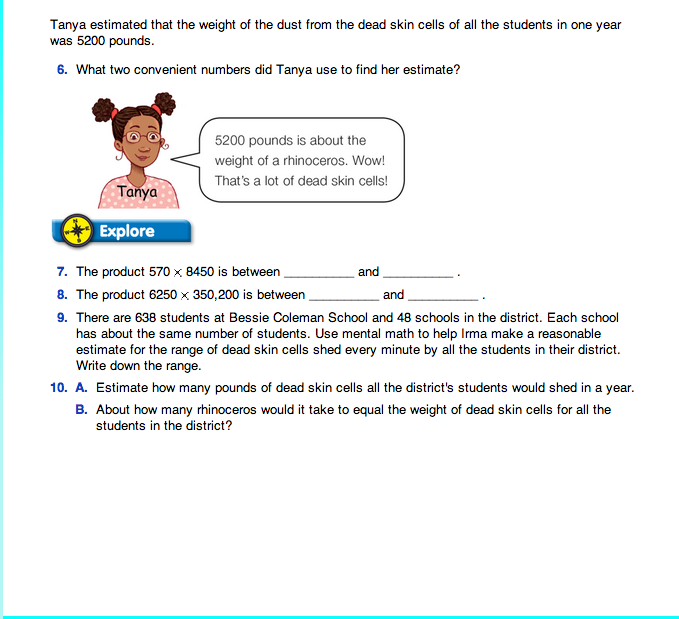
In Question 6, students are asked to identify the convenient numbers Tanya used to come up with her estimate of the 5200 pounds for weight of the dust of all the students' dead skin cells in a year. Students can use multiplication to think about this problem. Each person sheds about 8 pounds of dead skin cells in a year. They may suggest the number sentence: 8 × n = 5200. Students should recognize that the value for n will be a convenient number close to 638, the total number of students in the school. Students may first multiply 8 × 600 = 4800. Since 4800 is 400 less than 5200, they then can think 8 × n = 400 or 8 × 50 = 400. This is one way that students may use to figure out that Tanya chose 650 (rounding up from 638) as a convenient number to estimate 5200.

Questions 7–8 ask students to explore estimates as a range of possible numbers. Use these or similar questions to generate a class discussion.

Possible responses are given for Question 7:

X
  • How did you find the lower end of your range? (Possible response: I multiplied 500 × 8000 = 4,000,000.)
  • How did you find the upper end of your range? (Possible response: I used convenient numbers and multiplied 600 × 9000 = 5,400,000.)
  • Do you think the exact answer might be closer to the upper end or the lower end? Why? (Possible response: I think it is closer to the upper end. If you round 570 up to 600 and 8450 down to 8000 and multiply you get 4,800,000. Since that rounds both numbers to closer numbers, it will be a better estimate. 4,800,000 is closer to 5,400,000.)
  • Does your range give a close enough approximation of the product? (Possible response: Rounding to closer convenient numbers gives a better estimate.)

In Question 9, students are asked to estimate the range of dead skin cells shed every minute by all the students in the district.

Ask:

X
  • How did you find the low end of the range? The high end? (Possible response: To find the low end of the range I rounded the number of students to 600 and the number of schools to 50. Then I multiplied 600 students × 50 schools = 30,000 students. I multiplied 30,000 students × 30,000 skin cells = 900,000,000 to find the low end of the range and 30,000 students × 40,000 skin cells = 1,200,000,000 to find the high end of the range.)
  • Did anyone use a different strategy? (Possible response: I rounded the number of students to 650 and the number of schools to 50. Then I multiplied 650 students × 50 schools = 32,500 students. I multiplied 32,500 students × 30,000 students = 975,000,000 to find the low end of the range and 32,500 students × 40,000 = 1,300,000,000 to find the high end of the range.)

Question 10A asks students to estimate how many pounds of dead skin cells are shed each year for all the elementary students in the district, if each person sheds about 8 pounds a year. Solutions will vary and depend on which convenient number is used for the total number of students in the district. Two possible solutions follow:

8 pounds × 30,000 students = 240,000 pounds

8 pounds × 32,500 students = 260,000 pounds

For Question 10B, students can reason that if the weight of the dead skin cells for the students at Bessie Coleman School is equal to one rhinoceros, and if there are about 48 similar-size schools in the district, then the weight of 48 rhinoceroses will be about the same as the weight of the dead skin cells for all 48 schools.

Student Guide: 138 139 140
Answers
X
SG_Mini
+
X
SG_Mini
+
X
SG_Mini
+
Student Activity Book:
X
Master: