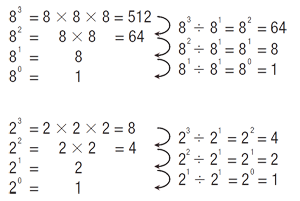Read Sand Reckoning. Direct students to the Exponents and Large Numbers pages in the Student Guide. This lesson begins with the story “Sand Reckoning.” In this story, Ellen, a fifth-grade girl, is raking the leaves in her yard. She tells her father that there must be a “zillion” or at least a billion leaves. He says that there are nowhere near that number. A neighbor is strolling by and stops to chat with Ellen. The neighbor, Mrs. Patel, is a scientist who works with very large numbers. She tells Ellen about the way very large numbers are written and about the “googol” (1 with 100 zeros after it—10100) and the “googolplex” (1 with a googol of zeros after it). Mrs. Patel also shares with Ellen the story of Archimedes' attempt to estimate the number of grains of sand in the universe.
Use Questions 1–3 in the Student Guide to introduce the story. Ask students to work in pairs to answer the questions. Encourage students to use calculators in their “reckonings” and then to use what they know about multiplying large numbers to decide if their answers are reasonable.
Questions 1 and 2 ask students to make the same estimate that Ellen's father makes in the story:
30 ft. × 50 ft. = 1500 sq. ft. in the yard
1500 sq. ft. × 100 leaves per sq. ft. = 150,000 leaves
To answer Question 3, students can use similar reasoning to estimate the number of leaves in Ellen's block and Ellen's town. Possible estimates for Questions 3A and 3B:
20 yards × 150,000 leaves per yard = 3,000,000 leaves or about 3 million leaves
and
300 blocks × 3,000,000 leaves per block = 900,000,000 leaves in town
As students work, ask them to read the numbers aloud and remind them to use the correct labels on their answers.
Ask students to read “Sand Reckoning” through, just to enjoy the story. Then choose some of the discussion prompts to bring out the mathematics in the story in a class discussion.
Page 147
- Describe a method for making a good estimate of the number of leaves in a yard. (Possible response: Count samples of leaves from a small area in the yard. Use the sample data to calculate an estimate for the number of leaves in the whole yard.)
- How much area do you think a billion leaves would cover? (Possible response: If each leaf is about three square inches, a billion leaves would cover almost 3/4 of a square mile, about 925 football fields, or about 50 city blocks.)
- Do you really think there are a billion leaves on Ellen's lawn? Is Ellen's estimate high or low? (Possible response: Unless Ellen's yard is almost 3/4 of a square mile, it is unlikely that there are a billion leaves in her yard. There are probably many fewer leaves in her yard.)
Page 148
- Find Sicily on a world map or a globe.
Page 149
- What does infinite mean? Why do you suppose some people might think that the number of grains needed to fill the universe is an infinite number? (Infinite means never ending, immeasurably great, or unlimited.)
Modern physicists and astronomers define a matter-universe roughly as an expanding sphere within which all matter is contained. The boundary of this sphere is considered the edge of the matter-universe. This could be imagined as an ever-expanding balloon with all existing matter inside. Archimedes' view of the universe is less clear but his calculations were remarkable for his time and the tools at his disposal.
Page 150
- What's a quick way to multiply 40 × 40 × 40 and 64,000 × 10,000? (Possible response: 4 × 4 × 4 = 16 × 4 or 64. Then, add on the zeros to get 64,000. To multiply 64,000 × 10,000, multiply 64 × 1, then add on 7 zeros to get 640,000,000 or six hundred forty million grains of sand.)
Provide students with an opportunity to test Archimedes' approximation. Place a small container of poppy seeds and several marbles in a work area for students. Invite students to use a line of poppy seeds to find the width of their finger. Ask students to answer the following questions:
- Is the width of your finger equal to 40 poppy seeds?
- Is your finger about the same width as a marble?
- Based on your experiment, do you think your approximation for the number of grains of sand in the universe would be bigger or smaller than that of Archimedes?
Page 151
Use a display to show students what a googol looks like. A googol is a 1 with 100 zeros after it. To show a googol, put a 1 on the display and ask several students to come up to add zeros to the number. Some possible ways to do this include asking four students to each add 25 zeros to the 1, asking five students to each add 20 zeros to the one, or asking ten students to each add 10 zeros to the one.
- How do you know there is a number larger than a googolplex? (Possible response: you can have a googolplex plus one. You can always add one to a number.)
- Do you think Archimedes' plan to estimate the number of grains of sand in the universe made sense? Why or why not? (Possible response: Yes, it made sense, because he started by estimating the number of grains of sand in a small area and then kept looking at bigger and bigger areas.)
- Explain how his estimate would be different today than it was in his lifetime. (Possible response: The number would be much bigger because we know the universe is larger than he thought it was.)
- Archimedes did all of his calculations by hand and so there was a greater potential for error. What technology do we have today that would have been helpful to Archimedes? (Possible response:
We have calculators and computers that can do the math, so it would be easier to find the estimate today than it was in his day.)
Represent Large Numbers with Exponents. Direct students to the Exponents section in the Student Guide. This page begins by revisiting Archimedes' estimate that it would take 1063 grains of sand to fill the universe. Have students read the introduction for using exponents to express numbers. Explain that when exponents are used, the number being multiplied is called the base. The number of times the base is multiplied is called the power of or exponent.
Ask students to look at each example in the Student Guide. Ask different students to read each example and to identify the base and the exponent or power. Encourage students to use correct language as they read each example. For 23 students should read “Two to the third power means 2 × 2 × 2. That equals 8. The base is 2 and the exponent or power is 3.” And, for 52 students read, “Five to the second power means 5 × 5 = 25. The base is 5 and the exponent or power is 2.”
Point out that when the exponent or power is 2, as in 52, the number can be read as “five to the second power” or “five squared.”
To provide additional practice write the following numbers on a display: 25, 63, 72, 81, 91 and 2471.
- What does 25 mean? (25 means 2 × 2 × 2 × 2 × 2 = 32. Encourage students to use correct language in their replies. For example: “Two to the fifth means two times two times two times two times two. That equals 32.” )
- What does 63 mean? (63 means 6 × 6 × 6 = 216.)
- What does 72 mean? (72 means 7 × 7 = 49. Point out that 72 can be read “seven to the second power” or “seven squared.”)
- What does 81 mean? What does 91 mean? What does 2471 mean? (8 to the first power means 8. 91 means 9. 2471 means 247.)
After students are comfortable finding the value of a number represented with an exponent, write the following number sentences on a display:
10 × 10 × 10 × 10 × 10 = n
3 × 3 × 3 × 3 × 3 × 3 = n
- What is the value of n in the number sentence 10 × 10 × 10 × 10 × 10 = n? (100,000)
- How can you represent this number using an exponent? (100,000 = 105)
- What is the value of n in the number sentence 3 × 3 × 3 × 3 × 3 × 3 = n? (729)
- How can you represent this number using an exponent? (729 = 36)
- How did you decide what number to use as the exponent in each of these numbers? (Possible response: You look at how many times you multiply the base and that is the exponent.)
Direct students to work with a partner to complete Questions 4–5 in the Student Guide. In Question 4A, students should identify five as the base in 52 and two as the exponent. In Question 4B, three is the base and four is the power. For Questions 5A–C, ask students to share the number sentence they used to find their solution. For example, in Question 5A, students should multiply 4 × 4 × 4 = 64.
81 is 8. So what is 80? or 2430? Any number to the zero power is 1. One way to look at this is to look at the following patterns:
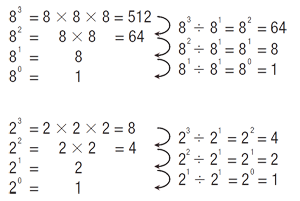
Try finding any number to the zero power on a calculator.
Calculators and Exponents. Different types of scientific calculators use different notation for exponents. Some scientific calculators use a caret (^) to denote exponents. Others use notation such as xy. Encourage students to learn to use the exponent key on their scientific calculators by following the manufacturer's directions.
Assign Check-In: Questions 7–11 to students. Students can complete these questions independently or with a partner.
Use Check-In: Questions 7–11 in the Exponents section of the Student Guide to assess students' abilities to write large numbers (to the billions) [E1]; represent numbers using exponents [E5]; and multiply numbers that are multiples of ten represented as powers of ten [E7].
After students have completed Questions 7–11, ask several students to describe the patterns they identified. See Figure 1.
- Why is the number of zeros in any power of ten written in standard form equal to the exponent? For example, why is 103 = 1000 and 104 = 10,000? (Possible response: Each time you multiply the number by 10 it gets ten times larger and so you add another zero, for example 10,000 is 10 times larger than 1000.)
- How much larger is each place in a number as you move from right to left? (Possible response: Since our number system is the base-ten system, each place in a number is ten times larger than the place to the right. So in a power of ten, each zero you add makes the number get 10 times larger or larger by one place.)