As students combine estimation and multiplication skills in this lesson, encourage them to do mental computations without calculators or paper-and-pencil methods.
Direct students to the opening vignette on the Estimate Products pages in the Student Guide. After reading the opening vignette together, discuss estimating with students. Explain that we often cannot or do not need to find exact answers—establishing a benchmark or using convenient numbers often provides an answer that works for the situation.
- What estimation strategies did Irma, Nila, and Tanya each use? (Possible response: rounding. They each rounded down from 21 classrooms to 20 classrooms and chose 30 as the benchmark for the number of students in each classroom.)
- Describe Irma, Nila and Tanya's methods. (All three methods use convenient numbers that are multiples of ten.)
Discuss each of the strategies presented. Irma uses a rectangle to create a visual model that shows each of the numbers decomposed into groups of ten before multiplying. Nila's method helps students see the place-value meaning of the zeros that are appended when multiplying multiples of 10. Tanya's method shows this mathematically using expanded form to show each number. She then reorders the factors to make it easier to multiply.
Have students work with a partner or in a small group to complete Question 1–4 before discussing them in class.
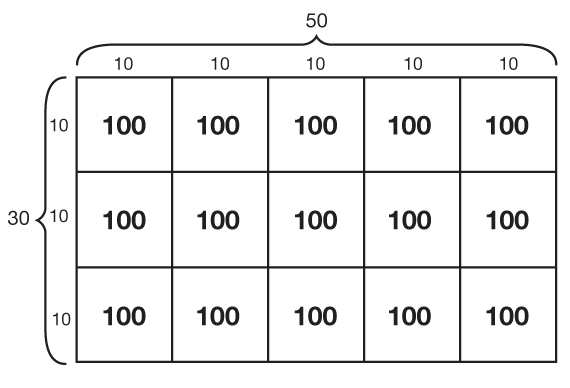
In Question 1, students describe the use of the commutative property for multiplication. Students should be able to describe the reordering of the facts to make the multiplication more efficient. In Question 2, students apply Irma's rectangle method to estimate 33 × 49. Students may round the numbers in the problem to 30 × 50 and solve with the rectangle method. See Figure 1 for one possible solution.
- In Question 3, how did you choose your convenient numbers to estimate the product of 71 × 58?
- Which multiplication method did you choose? Why?
In Question 4, students are asked to consider the efficiency of different methods.
- What makes Nila's method efficient? (Possible response: You can quickly multiply the numbers in your head.)
- Is Irma's rectangle method efficient? (It's not as quick as Nila's or Tanya's method, but it can help make sense of the problem.)
- Explain when using a calculator might be an efficient method and when it might not be an efficient method. (It is efficient when the numbers are not “friendly” or convenient or if they are very large numbers. But, if the buttons are pushed incorrectly a wrong answer may still result. We still need quick and accurate ways to find products mentally or by hand to check the reasonableness of our answers.)

Commutative Property of Multiplication. The commutative property of multiplication says that the order of factors in a multiplication sentence does not matter. Students may use the term turn-around rule instead of commutative property. Either term is appropriate here.
In order for students to appreciate the commutative property of multiplication, ask them to consider whether other operations are commutative. Addition is commutative (40 + 20 = 60 and 20 + 40 = 60). Division is not commutative: 60 cookies divided among 30 children gives two cookies per child (60 ÷ 30 = 20 cookies), but 30 cookies divided among 60 children gives only one-half cookie per child (30 ÷ 60 = 1/2 cookie).
The commutative property has to do with the order in which things can happen. Putting on your shirt and jeans is commutative (the order in which you do it does not matter), but putting on your shoes and socks is not (the order certainly does matter).
The commutative property is very useful when multiplying by multiples of ten. However, research shows that this is not always obvious to students. Students easily see that 3 × 20 is the same as 3 times 2 tens and can show it on the number line. However, when the problem is written 20 × 3, students may think of it as 20 hops of 3. This is correct, but changing the order of the factors first makes the problem much more efficient.