Stack Up

Launch the Problem. To begin this lesson, direct students to the Stack Up page in the Student Guide. Read the introductory vignette. In this vignette, Peter and Josh pose the question: How many pennies will you need to build a stack tall enough to reach the moon?

Divide the students so they are working with a partner or in a small group. Direct students to discuss Questions 1–3 with their group members. After students have had a few minutes to talk in their groups, ask several students to share their group's thinking.

For Question 1, students will need to know the thickness of one penny or the height of a small stack of pennies. For Question 2, students will likely identify that they will need pennies and a ruler to find the answer to this question. They should recognize that Josh is thinking about the distance from the Earth to the moon in kilometers, so they need to use a centimeter ruler to measure their pennies. This will enable them to easily convert between centimeters, meters, and kilometers. Students may also identify using a chart or table to look for patterns that they can use to help them find the solution.

In Question 3, students are asked to think about strategies that can be used to find out how many pennies you would need to stack to reach the moon. Encourage students to think about the strategies used by Archimedes to find the number of grains of sand needed to fill the universe in the story “Sand Reckoning” and those used by Emily's father to estimate the number of leaves in her yard in Lesson 4.

After the discussion, distribute a copy of the Stack Up Work Assessment Master to each student. Explain that though students will work with a partner or in a small group to complete the problem, each student is expected to record the group's work on his or her own paper.

Refer students to Questions 1–2 on the Stack Up Work Assessment Master. These questions ask students to collect information about pennies. Question 1A asks students to look at a centimeter ruler and predict the number of pennies in a stack of pennies with a height of 5 centimeters. After students have written their predictions, give each pair or small group twenty pennies so they can check their prediction for Question 1B.

Encourage students to work with their partner or group to complete this problem without your assistance unless a clarification question is needed.

After students have checked their predictions, ask them to solve Question 2. Have a few metersticks available for students. This visual representation of 100 centimeters might help some students check their estimates and calculations. Question 2B asks students to explain how they found the number of pennies in a stack one meter tall.

After students complete Questions 1–2, they will begin work on Question 3. Students can complete this question independently, with their partner, or with their small group using information gathered in Questions 1–2.

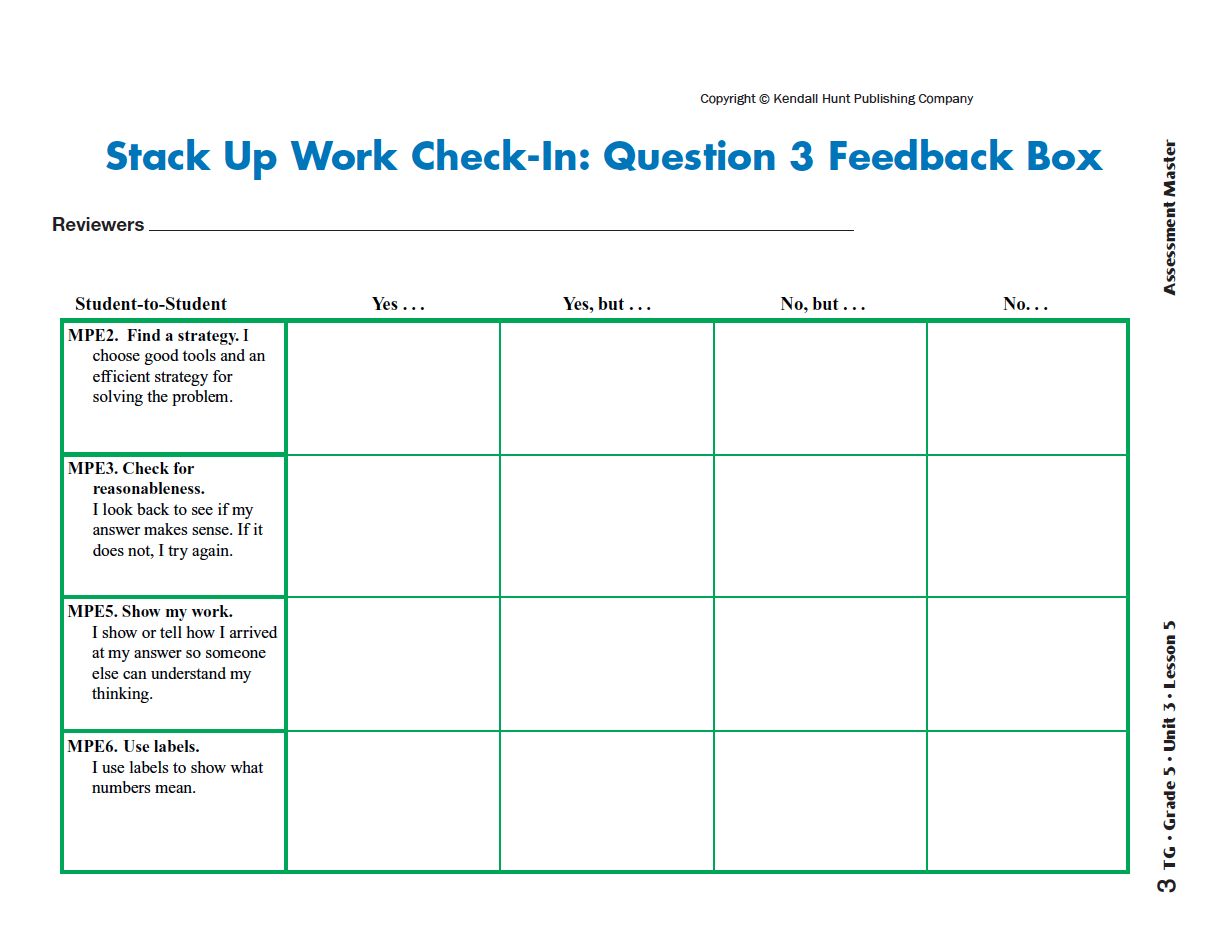
Before students begin their work, refer them to the Math Practices page in the Student Guide Reference section. Explain that for this problem students will focus on Math Practices Expectations 2, 3, 5, and 6. Read Math Practice Expectation 2 and then remind students that in the beginning of the lesson they discussed the kinds of tools and strategies that Josh and Peter could use to solve the problem.

Choose Strategies to Solve the Problem. When students are comfortable with the Math Practices Expectations, they can begin work on the problem.

This problem involves very large numbers so students may decide to round 384,400 to the nearest 100,000 (400,000) or 10,000 (380,000). Encourage students to use what they have learned about multiplying by multiples of ten as they solve this problem.

For example, if a stack of 35 pennies measures 5 centimeters, then there will be 70 pennies in a stack that measures 10 centimeters. Since there are 100 centimeters in a meter, then there will be 10 × 70 or 700 pennies in a one-meter stack. Since there are 1000 meters in a kilometer, there will be 1000 meters × 700 pennies or 700,000 pennies in a one-kilometer stack.

The average distance between the Earth and the moon is 384,400 kilometers, or 400,000 kilometers if rounded to the nearest 100,000. 400,000 kilometers × 700,000 pennies × 280,000,000,000 pennies to reach the moon.

Students may choose to use a calculator to help them solve this problem. Many four-function calculators will not be able to display the final results; however, students can use the calculator to support their paper and pencil solution. For example, if a student decides to round 384,400 to the nearest 10,000, or 380,000, they may write 380,000 as 38 × 10,000 and 700,000 as 7 × 100,000. They can then multiply 38 × 7 = 266. Students can then use paper and pencil to multiply 10,000 × 100,000 = 1,000,000,000 or 10⁹. Finally students multiply 266 × 10⁹ = 266,000,000,000. This strategy can also be used without rounding as shown in Figure 1.

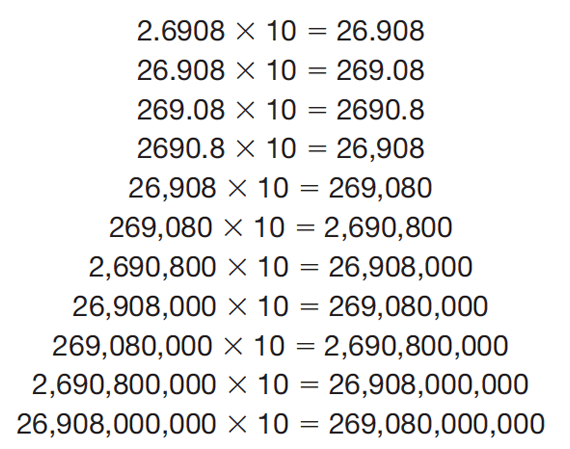
If students have access to and use a scientific calculator the answer in the display will be shown in scientific notation. For example, if students use a scientific calculator to multiply 384,400 × 700,000 the display might read 2.6908 11. The 11 on the calculator display tells you to multiply 2.6908 by 10, 11 times or 2.6908 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10. Each time you multiply by 10 the decimal point will move one space to the right. Zeros are added to each empty space created by moving the decimal point. See Figure 2.

Once a solution has been reached, students should write a clear explanation of their problem-solving process. Each student should write his or her explanation independently. Remind students to use the Math Practices page in the Student Guide Reference section to guide them as they write their explanation for Question 3.