Volume of Cube Models

Est. Class Sessions: 2–3

Developing the Lesson

Part 2: Cube Models

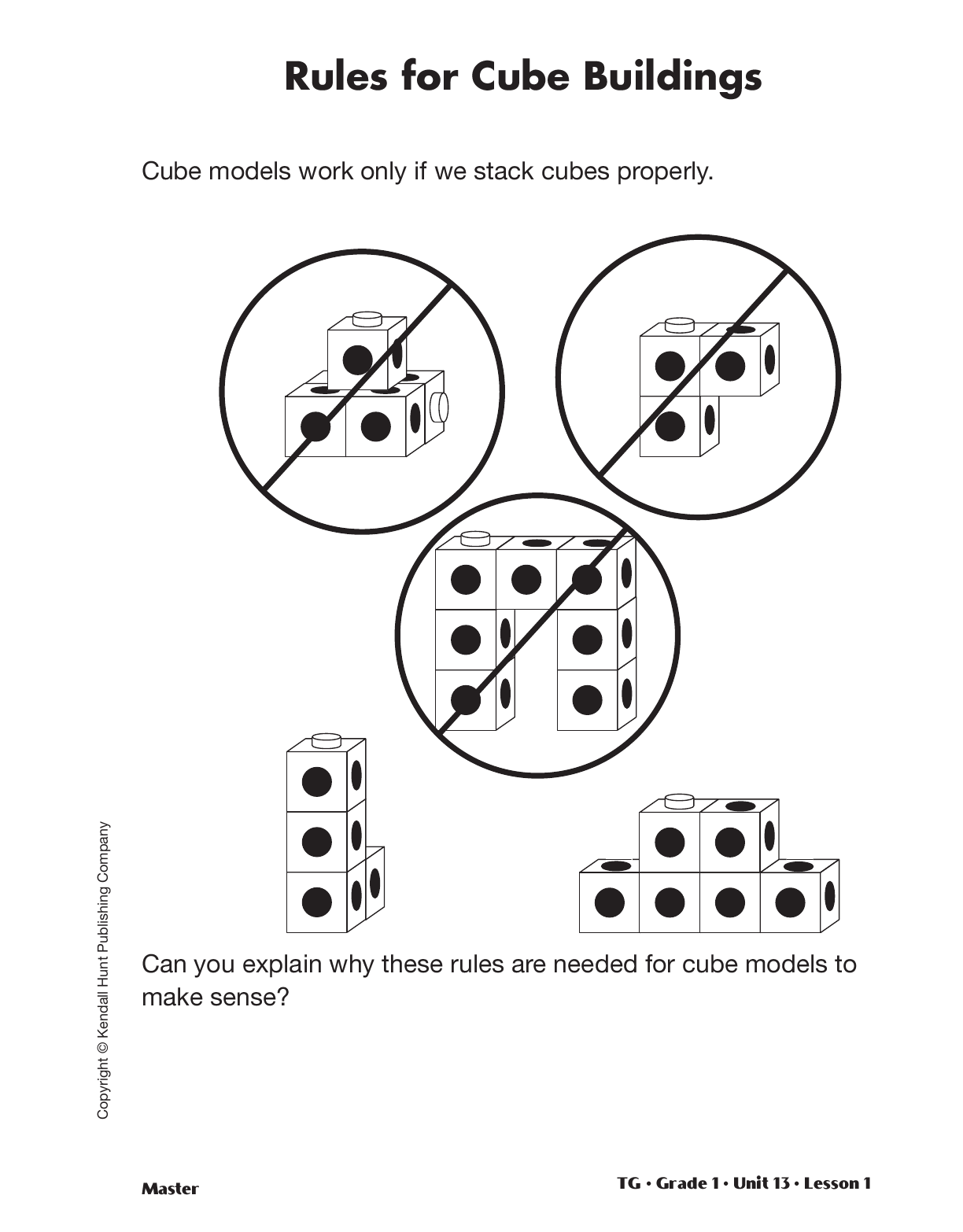
Build Models with a Volume of Eight Cubic Units. Tell students that they are each going to use eight connecting cubes to construct a building. Display the Rules for Cube Buildings Master. Ask students to look at the three pictures that are shown in circles with a line through them.

Ask:

Look at the buildings on this page. What do you think it means when a building is in a circle with a line through it? (Possible response: Those are the buildings that you are not allowed to make.)
What rules do you think there are for constructing your buildings? (Possible responses: All of the blocks need to be connected to each other side to side. You can’t make a building that has tunnels or bridges. A floor can’t be bigger than the floors below it.)

Direct each student to construct a building using eight cubes that follows these rules. Have the students observe their buildings from different vantage points: front, side, back, top, and bottom.

As you circulate ask these or similar questions:

Does your building look the same from each point of view?
How is it different?
How is it the same?
How many cubes are in your bottom floor?
How many floors does your building have?

As students finish their buildings ask them to compare their building with those of other students in their group.

Once everyone has finished building, ask:

Did anyone make a building with just one cube in the bottom floor or level? [If no one volunteers, continue the same questioning as a hypothetical.]
If you follow the rules for building, what does your building look like? (Possible response: The building is tall and skinny with one cube for each floor.)
How many floors does your building have? (eight)
How tall is your building? (eight cubes tall; See
Figure 4.)
Who made a building with two cubes on the bottom floor? How many cubes could you put on the next level? (one or two)
If you put only one cube on the next level, how tall would your building be? (seven floors tall) Explain why it will be 7 floors tall. (If there are two cubes on the bottom floor and one on the second floor you can only put one cube on all of the other floors. See
Figure 5.)
Who can describe another building that you can make that has two cubes on the bottom floor? (Possible responses: There are three more buildings that could be constructed: a building with four floors that has two cubes on each floor; a building with five floors, two cubes on the first three floors, and one cube on the fourth and fifth floors; or a building with six floors that has two cubes on the first and second floors and one cube on the third, fourth, fifth, and sixth floors. See Figure 5.)
How tall will a building be that has eight cubes on the bottom floor? (This building will only have one floor.)

Invite student volunteers to describe their buildings to the rest of the class. Encourage students to describe the number of cubes on each floor as well as the total number of floors for their building.

After several students have shared their buildings, ask:

Think about all of the different buildings you have made with your cubes. What is the volume of these buildings? (The volume of each building is 8 cubic units.)

If no student is able to identify that the volume of all of the buildings is the same use these or similar prompts.

How can you find the volume of your building? (You can count the cubes.)
How many cubes did each of you use to construct your building? (eight)
If each building is constructed from eight cubes, what is the volume of each building? (eight cubic units)

End the discussion by reminding students that the amount of space the building takes up is the volume of the building and to find the volume you can count the number of cubes used to construct the building.

Sort Buildings by Height. Tell students that they are going to use a second measurement—height—to organize their buildings. In this activity, height is expressed as the number of floors in the building. Remind students that they can describe the height using floors as a unit because the cubes are equal in size.

Have students sit in a large ring. In the center of the ring, place the eight large sheets of paper you prepared labeled with the number of floors 1 to 8. As you announce each number of floors, ask students to place their buildings on the paper that describes the height of their building.

Then pose questions similar to the following:

On which sheet do you see the greatest number of buildings?
Are there buildings that are alike?
How many buildings are alike?
What do we know about the volume of all those buildings? (They all have a volume of 8 cubic units.)
Why are they all the same volume when we've just said that some are different? (We built them all out of 8 cubes.)

Repeat the same type of questioning for other sheets of paper that have several buildings on them.

Encourage students to share their observations with the class as they compare and contrast the buildings displayed in the center of the ring. Students should establish the criteria for deciding what to consider alike and what to consider different.

Develop the idea that shape is independent of volume as shown by the variety of shapes made with a volume of eight cubes. Guide the discussion to help students generalize that any given volume (larger than two cubic units) can have a variety of shapes. Remind students of their work in Unit 8 Lesson 2 Goldilocks and the Three Rectangles and Lesson 4 Unit Designs. In those lessons students found that a variety of shapes can have the same area.

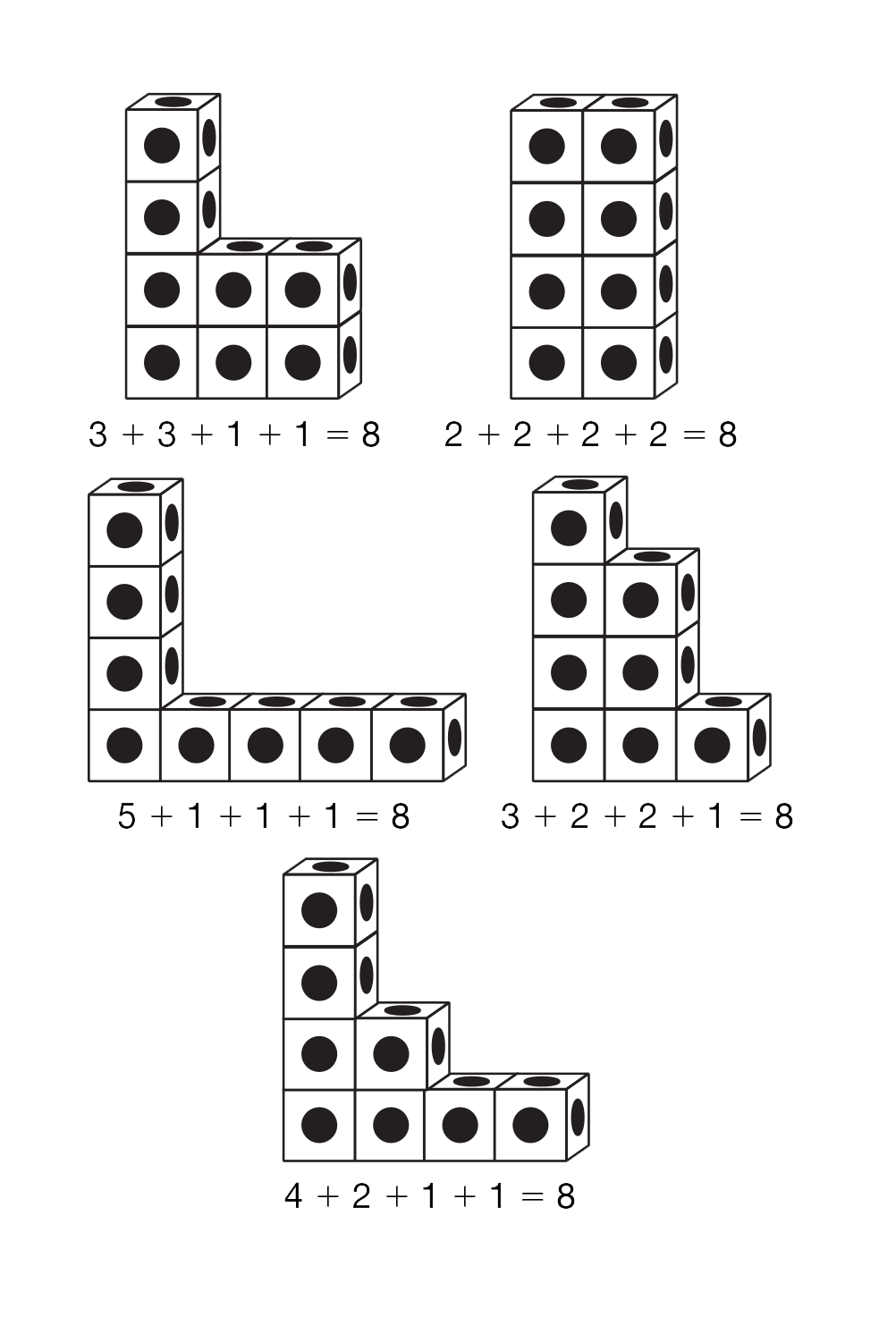
Discuss Writing Number Sentences for Buildings. Choose several different buildings that each have four floors. Tell students that they can write a number sentence that will describe the volume of the building. Choose one of the buildings from your selection and tell students that you will write a number sentence adding the number of cubes on each floor. For example, in a building that has 2 cubes on each floor, the number sentence will be 2 + 2 + 2 + 2 = 8 and for a building with three cubes on each of the first two floors and one cube on the third and fourth floors the number sentence will be 3 + 3 + 1 + 1 = 8. See Figure 6 for the number sentences for buildings with four floors. Repeat this activity with one or two more of the different buildings. Ask students to provide the number for each floor of the building as you write it in the number sentence. Record several of these number sentences on the board.

Then ask:

What is the same about all these buildings? (The volume is the same. The volume of each building is
8 cubic units.)
What is different about all these building? (The buildings are different shapes.)

Observe students as they sort and describe the buildings they constructed. Observe their ability to recognize that cube models with different shapes can have the same volume [E5].

It is possible to have two different buildings represented by the same number sentences. For example in a building with four cubes on the bottom floor the cubes can be arranged in 4 different ways: