Lesson 3

Strategies to Find Volume

Est. Class Sessions: 2

Developing the Lesson

Part 2. Cube Models with Some Cubes Hidden

Show the display of the TIMS Towers 2 Master.

Ask:

X
  • How are these towers different from the Tall Tower and the Sky-High Tower? (Possible response: These towers have some cubes that are behind other cubes on each floor, but the Tall Tower and Sky-High Tower have only a single row on each floor. These buildings are wider than the Tall Tower and Sky-High Tower. One of the towers is not a box. All the other ones are boxes.)
  • Can you build these towers by putting together all the cubes you see on the drawing but no others? Explain your reasoning. (Possible response: No, because there are some cubes in the back but we can’t see how many there are. We need more cubes than we can see on the drawing.)
  • Can you figure out the volumes of these buildings by counting the cubes you can see on the drawing? (Possible response: No because some of the cubes are hidden. We need to count all the cubes not just the ones that we can see.)

Direct students to the More Towers section of the TIMS Towers pages in their Student Activity Book. Show a display of the Rules for Cube Buildings Master from Lesson 1.

Ask:

X
  • How can you use the Rules for Cube Buildings to help you build these two towers? How do these rules help you think about the cubes that are hidden? (Possible response: The building rules show that the bottom floor of the tower has to be filled in with cubes and there can’t be holes in the middle. That means every column and every row is filled in so when we make the hidden rows we can’t leave any spaces.)

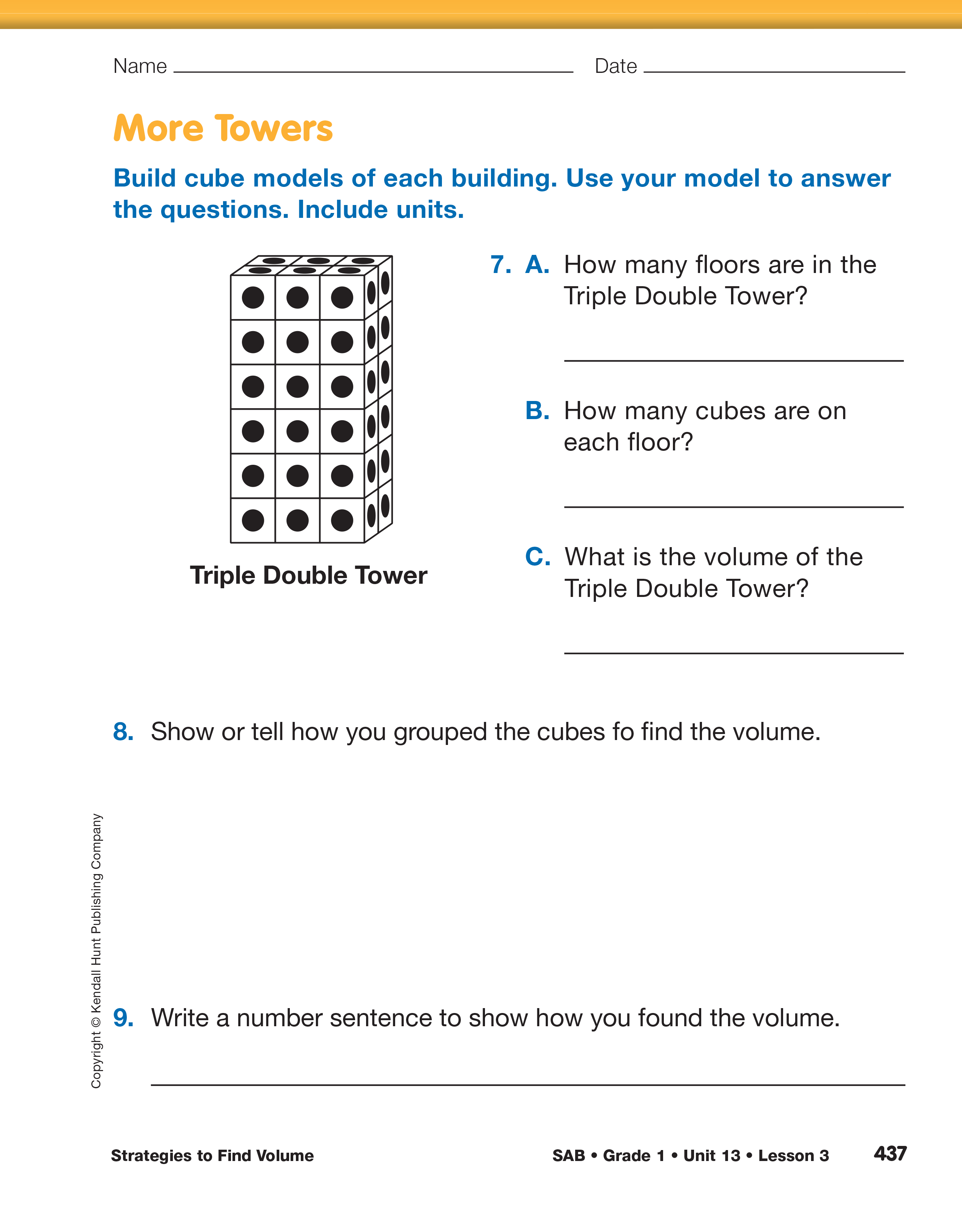
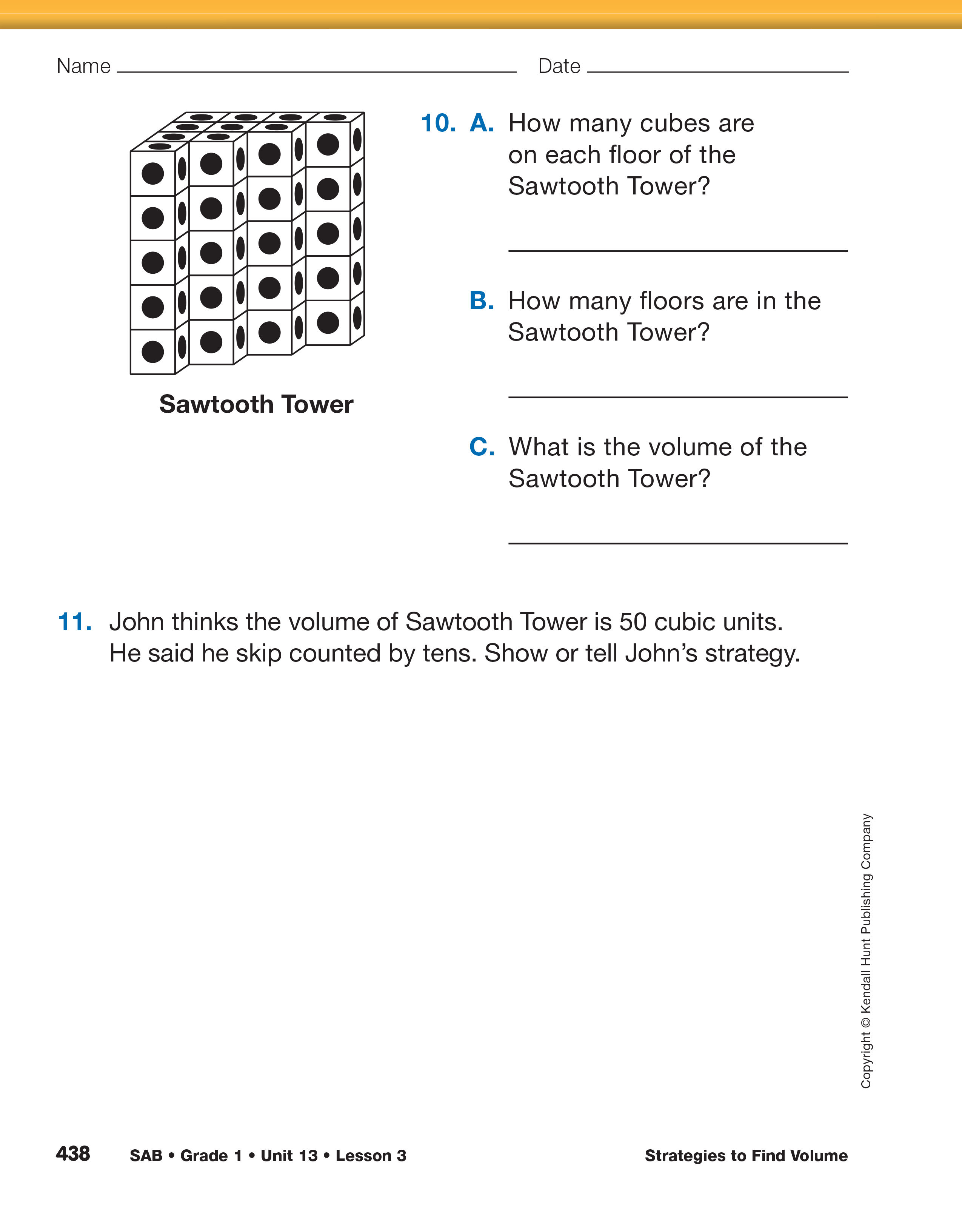
Provide time for students to work with their partner to complete Questions 7–11.

Students can take several different solution paths to find the volume of these towers. As you circulate through the class, note students using various strategies to include in discussion when work is done.

As students work through each problem, keep asking questions to foster use of a variety of strategies to determine the volume of each tower using prompts similar to the following:

X
  • Is there another way to find the volume?
  • If you look at your building from another side or from the top, can you see another way to count the cubes?
  • How can you break the tower into sections to help you find the volume?

When students have finished, conduct a class discussion eliciting the various strategies used to find the volume of the two towers. Foster discussion to include various decomposition strategies (grouping by columns and breaking towers into rectangular prisms) and various counting strategies (counting by tens and counting on, skip counting by twos, threes, fives, or tens, doubling, and using repeated addition on the calculator).

The Sample Dialog shows a possible discussion of strategies used to find the volume of the Triple Double Tower.

X

Use this sample dialog to help guide the classroom

discussion about strategies used to find the volume of

each tower.

Teacher: Jackie, what strategy did you and Linda use to find the volume of the Triple Double Tower?

Jackie: I counted the cubes that are showing on the front of the building and got 18 cubes. We knew that there are also 18 cubes in the back of the building, so Linda used the calculator to add 18 + 18 and found the volume equals 36 cubic units.

Teacher: So you divided the tower into two parts and used doubling to find the volume. Did anyone else use a different strategy?

John: We counted 6 cubes on each floor and there are
6 floors, so we used the calculator to add
6 + 6 + 6 + 6 + 6 + 6. We also got a volume of 36 cubic units.

Teacher: Great, you divided the building into floors and used repeated addition.

Ana: We also used the calculator to add
6 + 6 + 6 + 6 + 6 + 6, but we divided the building a different way.

Teacher: Ana, can you explain how you divided the building?

Ana: We divided the building into columns. There are
6 columns and there are 6 cubes in each column.

Teacher: You have found 3 different ways to divide the Triple Double Tower to find the volume. Is there anyone who has a fourth way to divide the building to make it easier to find the volume?

Luis: We divided the building into columns but we divided it into 3 columns with 12 cubes in each, so we added
12 + 12 + 12 to get the volume of 36 cubic units.

Teacher: You found several ways to divide up the Triple Double Tower so you could use doubling and repeated addition to find the volume. Let’s talk about the strategies you used to find the volume of the Sawtooth Tower.

Adventure Book:
Student Activity Book: 437 438
Answers
X
SG_Mini
+
X
SG_Mini
+
Master: