Use Cubes to Build Gates. Introduce the lesson by
telling students that you are going to tell them a
story about a boy named Manuel and his dog Ruffy.
It was a beautiful spring day and Ruffy wanted to be
outside. But Manuel had to do his homework and he
was afraid that Ruffy would run away or get lost if
he was outside by himself. Manuel’s mother had an
idea. “We have some extra blocks left over from
Dad’s last project. Ruffy can’t jump very high, so
why don’t we put some blocks down to make a pen
for him in a corner of the yard. Three walls of the
pen will be the backyard fence. We will only have to
build the fourth wall. It will be like a gate. Then
Ruffy would be able to lie in the sun and we wouldn’t
have to worry about him getting lost.” Manuel
thought that was a good idea, so he and his mother
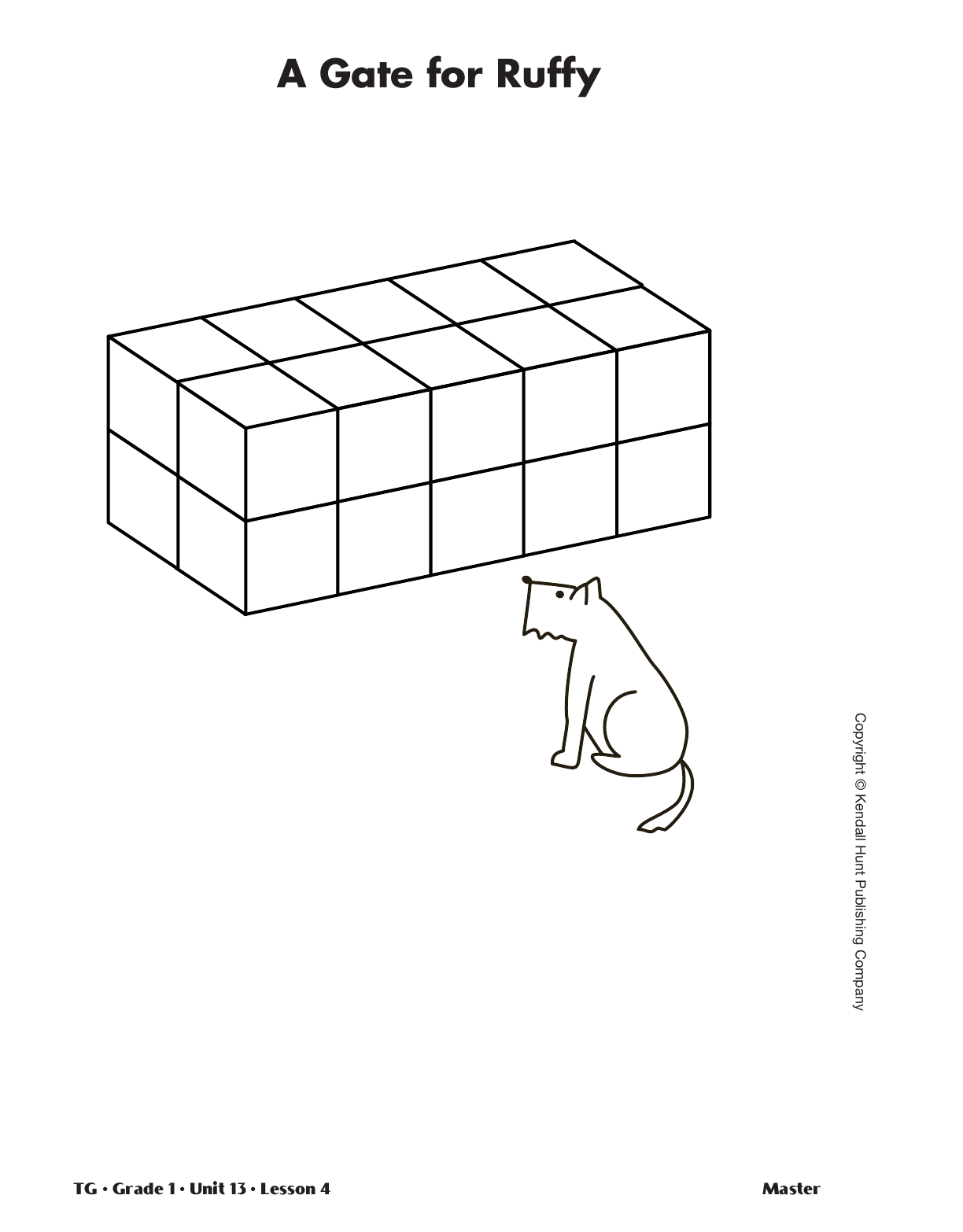
went out to build the gate for Ruffy. They built a wall
with 2 rows of blocks. Each row was 5 blocks wide
and
2 blocks tall.
Show the display of A Gate for Ruffy Master.
- What kind of block do you think they used? (possible responses may include: concrete blocks,
wooden blocks, connecting cubes) Are they still cubic units? (yes)
- Can someone explain what we mean by a cubic unit? (a cube that is one unit wide by one unit tall by one unit long)
Have students build Ruffy’s gate out of connecting cubes.
- What is the volume of Ruffy’s gate? (20 cubic units).
- What strategy did you use to group and count the cubes?
Encourage students to share different grouping and
counting strategies. As they share, record the strategies
and number sentences that represent the strategy.
See Figure 1 for two possible strategies.
Show the display of A Gate for Gruffy
Master. Tell students Gruffy is a bigger dog and needs a bigger gate. Have students build Gruffy's gate using connecting cubes.
- What is different about Gruffy’s gate? (It is taller and wider.)
- How many cubes wide and how many cubes high is it? (6 cubes wide and 3 cubes high.)
- Who has a suggestion for how we can group the
cubes and find the volume of Gruffy’s gate without
counting by ones? (Possible responses: We can
group by rows. There are 6 cubes in each row
and there are 3 rows, so we can add
6 + 6 + 6 = 18. Or, we can group by columns
and add 3 + 3 + 3 + 3 + 3 + 3 = 18. You
could also divide the building in middle. There
are 9 cubes on each half so you can double 9;
9 + 9 = 18.)
Repeat with skip counting by six or doubling nine.
- Compare Gruffy’s gate to Ruffy’s gate. Which gate is taller? (Gruffy’s gate)
- Which gate has the greatest volume, Ruffy’s or Gruffy’s? (Ruffy’s gate)
- What is the difference in volume between Gruffy’s gate and Ruffy’s gate? (2 cubic units) How did you
find your answer? (Possible response: I started on 18 and counted up 2 to 20. Or, I counted back 2 from 20 to get to 18.)
Write Number Sentences to find Volume. Direct
students’ attention to the Skip Count and Add pages
in the Student Activity Book. Have students work
with a partner to completed Questions 1–5. Students
use cubes to build a cube model of each shape. They
then find a way to group the cubes and use skip
counting to find the volume. Students write a number
sentence to represent their solution paths. In
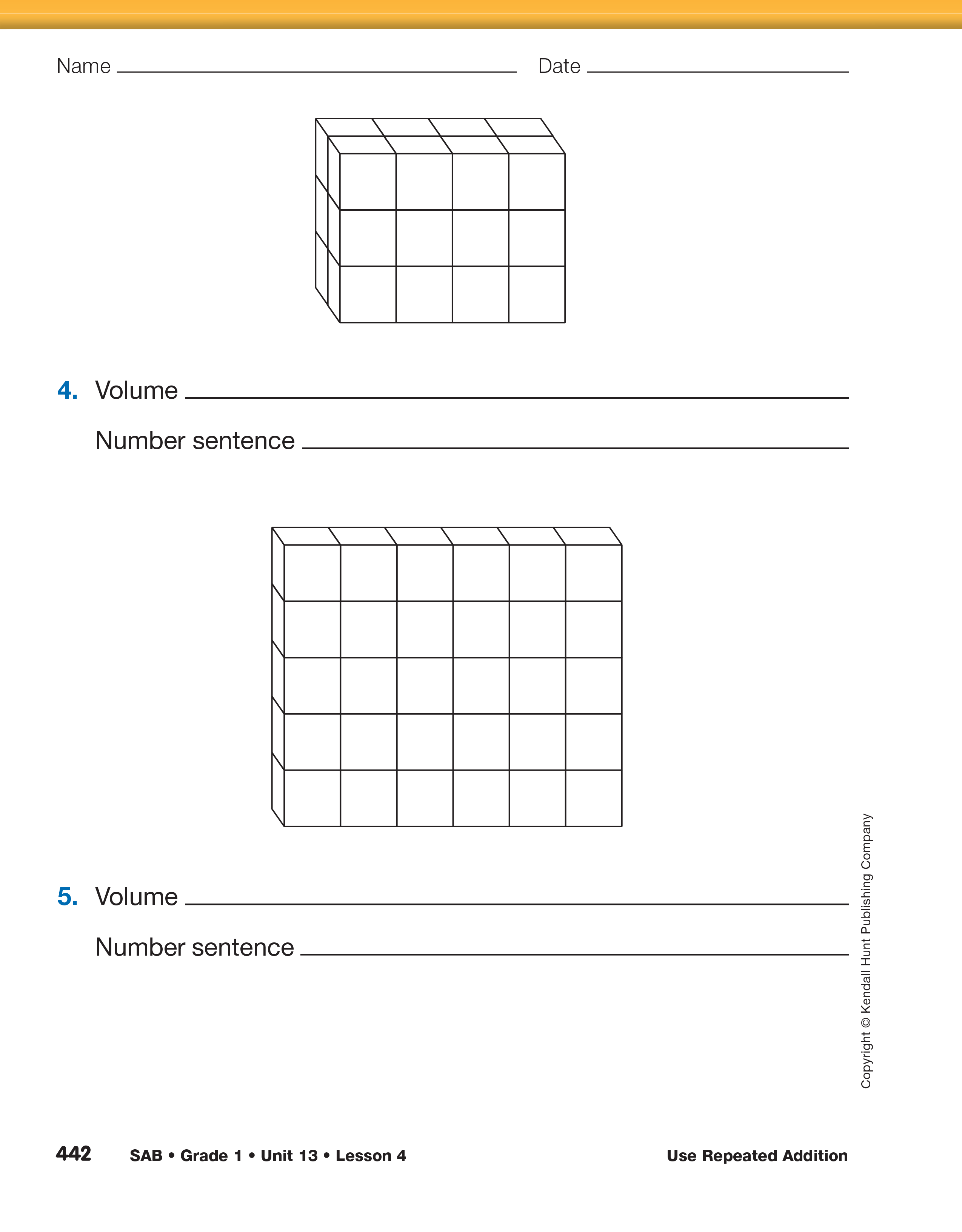
Question 1 the volume of the shape is 20 cubic
units. Students can group the cubes by rows and skip
count by 5s (5 + 5 + 5 + 5 = 20), or they can
group by columns and use their calculator to add
4 + 4 + 4 + 4 + 4 = 20. Students might also see
that if they divide the shape in half they can double
10 (10 + 10 = 20) to find the volume. In Question 2
the shape has two rows of cubes for each floor or
layer. In Question 2 Students can group the cubes by
the rows in front and the rows in back and count by
5s (5 + 5 + 5 + 5 = 20) or they can group the cubes
by layers or floors and count by 10s (10 + 10 = 20).
Students might also group by columns in front and
columns in back and count by 2s
(2 + 2 + 2 + 2 + 2 +
2 + 2 + 2 + 2 + 2 = 20).
After students complete the page, have them share
their strategies to find the volume of each shape. Ask
them to explain how they grouped the cubes to find
the volume. Record their number sentences by writing
them on the board or on a display. See the
Sample Dialog box.

Use this sample dialog to guide a class discussion about the
strategies and number sentences students used to find
the volume.
Teacher: Irma, what number sentence shows how you found the volume of the shape in Question 3?
Irma: 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 24.
Teacher: Can you explain how you grouped the cubes to help you decide?
Irma: First I grouped the cubes by columns. There are three
cubes in each column and there are 8 columns, 4 in
front and 4 in back. So I used my calculator to add 3
eight times and the answer was 24.
Teacher: Is there another way to group the cubes?
Irma: I grouped the cubes by rows. There are 6 rows, 3 in
front and 3 in back and there are 4 cubes in each row,
so it is 4 + 4 + 4 + 4 + 4 + 4 = 24.
Teacher: Did you use your calculator to find the answer to that number sentence also?
Irma: Yes, I don’t know how to skip count by fours so I used the calculator.
Teacher: Did anyone else use a different number sentence for Question 3?
Jacob: I used 12 + 12 = 24.
Teacher: Can you explain how you grouped the cubes?
Jacob: I counted the cubes on the front of the shape and got
12. I knew there were also 12 on the back of the shape
so I doubled 12.
Teacher: Good, are there any other ways to group the cubes for this shape?
John: I did 6 + 6 + 6 + 6 = 24 on my calculator because I
also grouped the cubes by columns, but I counted both
rows of cubes as one column.

Some students may already be familiar with multiplication
number sentences and may suggest a sentence like
6 x 4 = 24.
Accept this sentence also and write it on the board or display.
Ask the student what he or she understands by the word
“times” in the sentence. Elicit a short conversation that draws
parallels to the class discussion about adding 4 six times, i.e.,
about repeated addition.
After discussing student solutions, remind students
that there are many ways to group the cubes and use
repeated addition to find the volume that are more
efficient than counting each one of the cubes.
Read A World of Cubic Animals. Remind students
about the short story about Manuel and Ruffy you
shared at the start of the lesson. Tell them that they
are going to read another story about Manuel and his
strange world of cubic animals. Read and discuss A
World of Cubic Animals in the Adventure Book
together. As you read, have a general discussion
about the story and the animals Manuel encounters.
It is not necessary to ask students to find the specific
volume of the cubic animals as this is something
they will do at the conclusion of the story. Use these
or other general discussion prompts to talk about the
story as you read.
Page 2
- How does Manuel know that the two different shapes he made have the same volume?
(Possible response: He counts the cubes in each building to find the volume).
Page 4
- What happens when Manuel goes to bed? (Possible response: He has a dream and Ruffy is made out of cubes.)
Page 5
- Where is the first place Manuel visits in his dream? (He visits Farmer Jones on his farm.)
Page 7
- What is the volume of each of the horse’s legs? (Each leg of the horse has a volume of 8 cubic units, including the hooves.)
- Which is an easier way to find the volume of the horse’s legs, counting by ones or counting by twos? (counting by twos)
- What is the volume of all four of the horse’s legs together? (32)
- How did you find your answer? (Possible response: I counted by twos to find one leg; 2, 4,
6, 8. Then I used the calculator to added 8 + 8 + 8 + 8 = 32 for the
four legs.)
Page 9
- Where did Manuel and Ruffy go to find other animals? (the zoo)
Page 12
- What is the volume of the giraffe’s neck? (12 cubic units)
- What strategy did you use to find your answer? (Possible response: I counted by twos: 2, 4, 6, 8, 10, 12.)
- Do you think a real giraffe has the same volume as the cube giraffe? (No, a real giraffe would have a much larger volume.)
Page 22
- Why does Manuel say it is easy to find the volume of things made of cubes? (Possible response: He
can group the cubes and use skip counting and adding to find the volume.)
- What is the volume of the dog bone in Ruffy’s dream? (The dog bone is 9 cubic units.)
If children compare the animals’ volumes to one another, you
can discuss this observation by posing the following
questions: Do these animals compare in volume to one
another in the same way as animals you would see in real
life? Do you think that Manuel would have approximately the
same volume as a giraffe? Does a horse have about the same
volume as an elephant? Emphasize that because Manuel is
dreaming, things appear differently than they do in real life.