Addition and Subtraction Problems with Larger Numbers

Students expand their use of strategies such as counting on and making ten to problems such as 28 + 3, 25 + 20, and 23 + 7. They use connecting cubes, number lines, ten frames, and 100 Charts to extend their reasoning to larger numbers. For example, to solve 28 + 3, students can count on three from 28 mentally or use a number line. To solve 25 + 20, they can use a 100 Charts to count on from 25 by tens or think of counting coins (a quarter and two dimes). For 23 + 7, students can fill in two full ten frames and three more boxes, then fill in seven more boxes for three full ten frames. Alternatively, they can think of 23 as 20 + 3 and reason that 23 + 7 = 20 + 3 + 7. Since
3 + 7 = 10, 20 + 3 + 7 = 20 + 10, or 30.

Multiplication and Division

Research evidence shows that students as young as ages five to six are able to solve problems involving repeated addition (multiplication) or subtraction (division) concepts if the problems relate to familiar situations and can be represented using manipulatives and pictures.

This unit expands and strengthens students' inherent multiplication and division problem-solving capabilities using the following key features:

• Building upon students' knowledge of multiplication and division concepts with engaging activities and interesting problems
• Presenting problems using everyday situations and everyday language
• Encouraging a variety of thinking strategies for solving problems

Computational skills, such as memorization of facts and calculation with multidigit numbers, are not a focus of this unit. Knowledge of the math facts comes after conceptual development is established.

This unit generally considers multiplication as repeated addition. For example, "If four students each have three pencils, how many pencils are there in all?" The number sentence for the solution is 3 + 3 + 3 + 3 or 4 X 3. Students use similar thinking processes to solve multiplication and division problems. For example, students explore the relationship between doubling a number (multiplying by 2) and finding half of a number (dividing by 2). In second, third, and fourth grades, we will introduce other ways for students to think of multiplication.

The division problems that students will solve fall into two basic categories: division by sharing and division by measuring out.

• Division by sharing includes problems such as "There are 18 pencils to be shared by three students. How many pencils will each student get?" Reworded, this problem becomes "If 18 pencils are divided into three groups, how many pencils are in each group?"
• Division by measuring out includes problems such as "There are ten pencils. Each math student needs 2 pencils. How many students can have pencils?" In other words, "If ten pencils are divided into groups of two, how many groups are there?"

In both categories, students know how many in all and want to find out about equal groups. It is not important for students to distinguish between the division categories. What is important is that students experience each.

This unit has dual emphases. First, as students solve problems, they are encouraged to think of various solution strategies. Second, students share problem-solving strategies with their class. It is important for students to generate their own strategies and choose their own tools, so that they can clearly articulate the methods they use. In this way, they will have a solid foundation for developing more efficient computational procedures that are based on number sense and the concepts underlying the operations. Figure 1 shows student solutions from the same first-grade class for the following problem, "A dog's owner cooked some meat that had two bones in it. How many bones would the dog have if the owner cooked the same kind of meat every day for a week?"

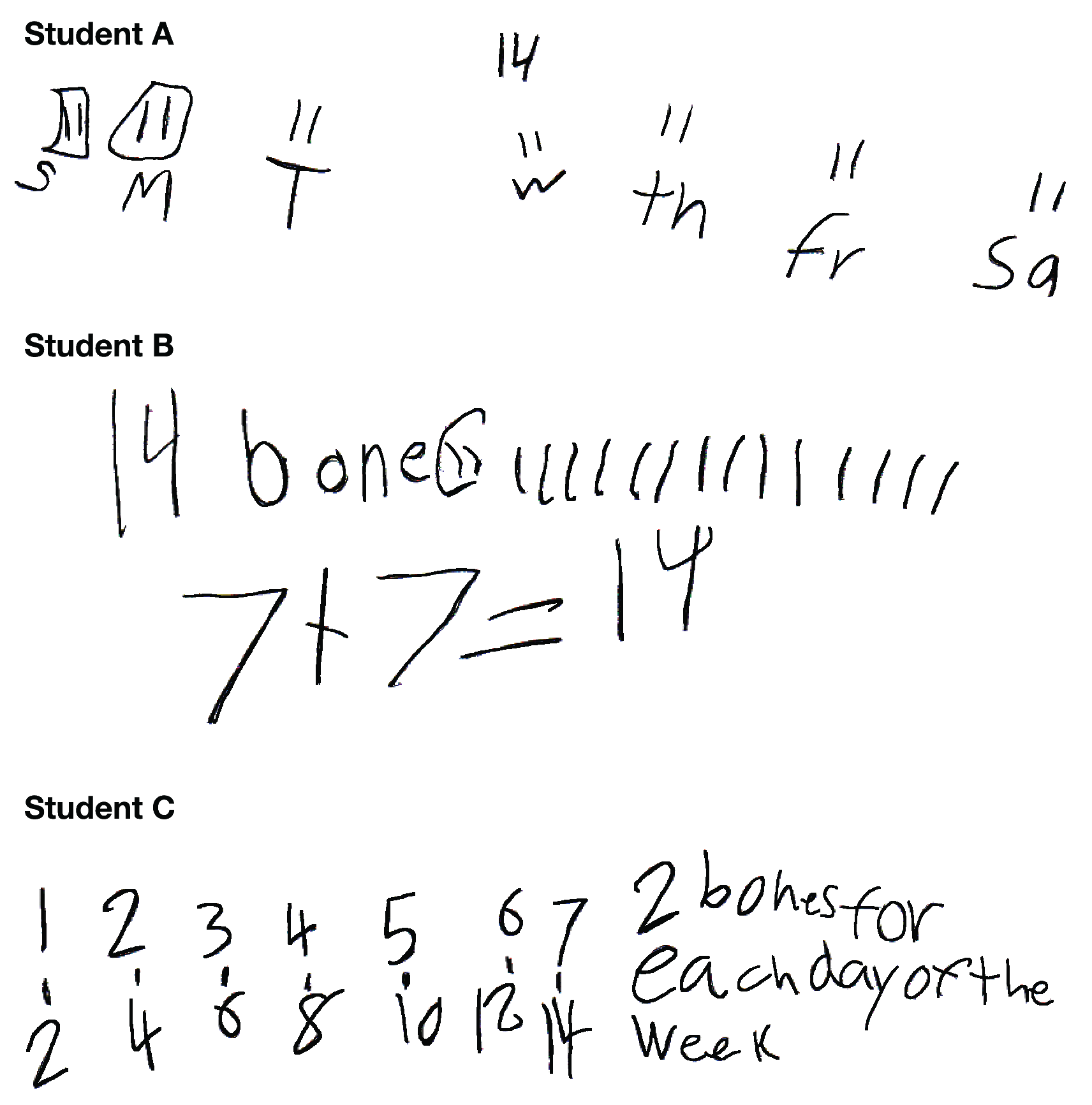
Figure 1: Three first-grade solutions to the same problem

Addition Facts with Sums to Ten

In this unit students continue to systematically review the addition facts. Daily Practice and Problem items in this unit can be used to assess students' fluency with the addition facts with sums to ten in Group C (1 + 9, 2 + 7, 2 + 8, 3 + 6, 3 + 7, 4 + 6, 5 + 5). Students should also be developing reasoning strategies to solve the addition facts with sums larger than ten in Group C (2 + 9, 3 + 8, 4 + 7, 5 + 6). The making ten and using ten strategies are strategies commonly used to solve these facts.

Fact Families for Addition Facts with Sums to Ten

Students have been connecting addition to subtraction and using the addition facts to solve subtraction problems since Unit 6. A Students proficient with their addition facts can also find the related subtraction facts. Daily Practice and Problems items in this unit can be used to assess students' abilities to name the fact families related to each fact with a sum to ten in Group C. As students develop fluency with the facts with larger sums they will be able to name the related facts in the fact family.

Resources

• Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically: Integrating Arithmetic & Algebra in Elementary School. Heinemann, Portsmouth, NH, 2003.
• Carpenter, T.P., and J.M. Moser. "The Acquisition of Addition and Subtraction Concepts in Grades One through Three." In Journal for Research in Mathematics Education, 15 (3), 1984.
• Council of Chief State School Officers. Common Core State Standards for Mathematics, 2010.
• Worth, Joan. "Developing Problem-Solving Abilities and Attitudes." In Mathematics for the Young Child, J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.