Describe Squares and Rectangles. Begin by showing
students the square and non-square rectangles you
cut out before class. See Materials Preparation.
- What do we call these shapes? (a square and a rectangle)
- How are they alike? (They both have 4 straight
sides and 4 square corners. All the corners are the
same shape.)
- How are they different? (The non-squares have two
short sides and two long sides, but the square's
sides are all the same length.)
As students describe squares and rectangles, list the
descriptions on chart paper.
- What is a rectangle? (a shape with 4 sides and
4 corners; all the corners look the same; a rectangle
can have sides that are not the same length)
- What is a square? (a shape with 4 sides and 4 corners;
all the sides and corners are exactly the
same)
- Who can use a ruler to measure the sides of the
square? Are they all the same length? (yes)
- Does a square have 4 sides and 4 of the same corners? (yes)
- Is a square a rectangle? How do you know? (Yes;
it has 4 sides and 4 corners. Its sides are all
the same length, so it is a special rectangle.) [See
Content Note.]
- All squares are rectangles, but are all rectangles
squares? How do you know? (No, not all rectangles
are squares because some rectangles have
sides that are not all the same length. A square's
sides are all the same length.)

Squares and Rectangles. Students often think that a
square is not a rectangle. They believe that all rectangles
have one side longer than another. This may result from the
fact that almost every shape they see labeled as a rectangle
has one side longer than another. However, a rectangle is
a shape with four sides and four right angles. A square
also has four right angles and is, therefore, a rectangle.
A rectangle with congruent sides is a square. This means
a square is a special rectangle.
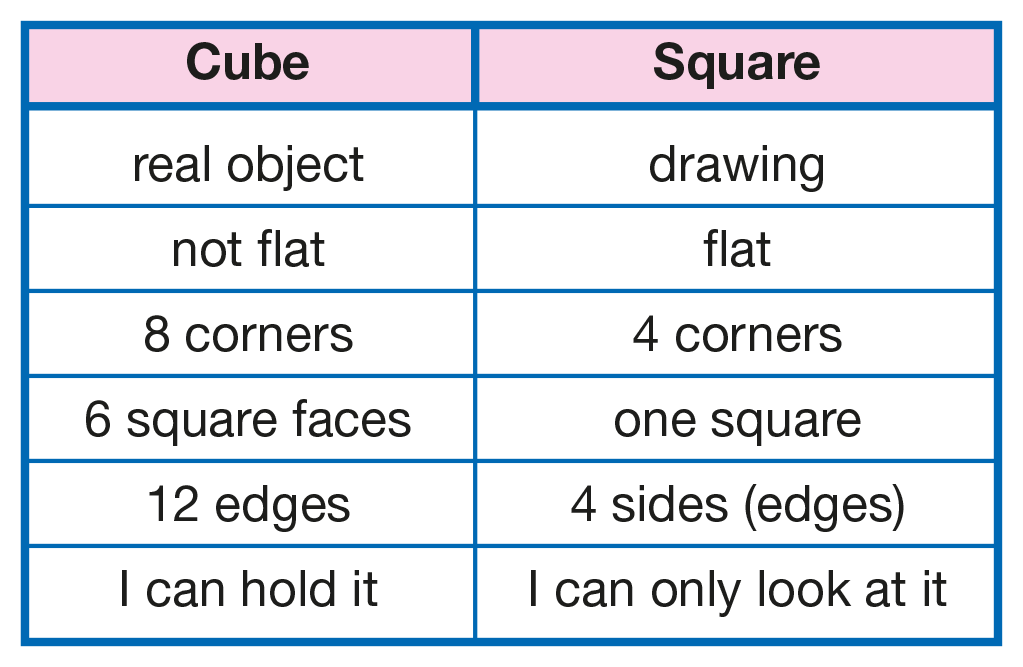
Describe Cubes. Distribute a cube to each student
pair. Ask students to look carefully at the cube.
- Describe the cube. Tell me in words what it looks
like. (Possible responses: It doesn't look flat; it has
length, width, and height; it looks like a lot of
squares put together; it has corners; it has 6 faces;
it looks like a die; it has straight sides; the four
edges of each face are all the same length)
- Who can use a ruler to measure the edges of the
cube? Are they all the same length? (yes)
Students may begin by talking about the holes and
bumps. Guide them to a discussion of the characteristics
that make an object a cube. Write student comments
on another piece of chart paper and use the
comments to make distinctions between the cube
and the square. See Figure 1 for guidance on the
comparison.
Define Same Shape. Tell students that in this unit
they will be putting connecting cubes together to
make structures that are called "buildings." Link
four connecting cubes horizontally and stack four
other connecting cubes vertically. See Figure 2.
Have students build the same two structures.
Hold
up your two structures keeping the horizontal and
vertical orientations and ask:
- Are these buildings the same shape or are they
two different shapes? (same shape) Why?
Let the students discuss this in small groups for a
few minutes. Then have the groups explain to the
class what they decided and why. Lead students to
an agreement that these two are the same shape.
- If I turn this [horizontal] to stand on end [like the
vertical structure], did anything change about its
shape? Is it still the same shape? What stayed the
same? (The way you are holding it is different. It
still has four cubes all in a row like the other
one.)
Tilt the structure slightly, so it is neither horizontal
nor vertical. Ask:
- Now, is this the same shape or is it a different
shape? (same shape)
- Can we agree that this is the same shape regardless
of how we hold it in space? (yes)
Have the class come to the understanding that two
shapes are the same shape if one can be turned or
rotated to look identical to the other.
Make Shapes with Four Cubes.
Present students
with the following problem:
- How many different shapes can you make using
four connecting cubes?
Have student pairs make the buildings and find as
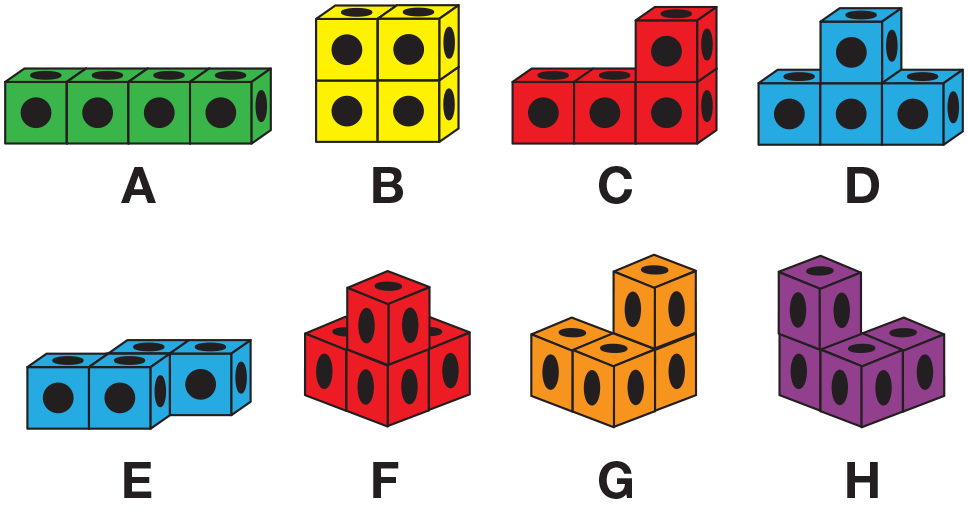
many possible solutions as they can. Figure 3 shows
the eight shapes that are possible using four connecting
cubes. See Content Note.
Mirror Images. Note that Shapes G and H in Figure 3 are
mirror images of each other. If you only look at the pictures,
you might think they were the same shape, only in different
positions. However, you cannot move one so it is exactly
like the other. This is a fairly subtle idea, and since it is
likely that some of your students will have difficulty with
visual reversals, you may not want to belabor this point.
As the students are working, circulate and ask questions
such as:
- How are you checking to make sure that you are
not making the same shape twice? (Possible
response: I turn it, flip it, and spin it around.)
- How is this shape different from this one?
Ask this for shapes that are the same as well as for
ones that are different.
- How is this shape like this one? (Possible
responses: same number of cubes; both are
straight; both are not straight; both are like a
square)
- How do you know when one shape is different
from another? (Possible response: Even when I
turn it, flip it, or spin it, it looks different.)
- Can you describe your shape with a number
sentence?
Arrange your cubes as in Shape A from Figure 3.
Show this building to the students.
- How would you describe this building in words? Use words like rows, columns, height, front, back,
left, and right. (Possible responses: It is straight;
all the cubes are in a row; all the cubes are in a
column; it is "all up and down".)
- If you had to write a number sentence about this
building, what could you write? Show us how the
numbers in the sentence match the cubes in the
building. (Possible responses: 1 + 1 + 1 + 1 = 4,
4 + 0 = 4, 0 + 4 = 4, 2 + 2 = 4)
- How did you use marshmallows to find the volume
of containers in Unit 5? (We filled them with
marshmallows and counted the number needed to
fill the containers.)
- Let's change the unit from marshmallows to cubes
or cubic units. How many cubes or cubic units are
in this building? (4 cubes or 4 cubic units)
- What is the volume of this building? (4 cubic units)
- How did you find the volume? (Possible
responses: I added the numbers in the number
sentence. I counted the cubes.)
- What important label should you include so, you
know what the numbers mean? (cubic units)
Now arrange the cubes as in Shape D from Figure 3.
Show this building to the students.
- How would you describe this building in words? (Possible responses: There is one on top and
three in a row on the bottom; it goes one cube,
then two cubes, then one cube; it has a column of
1, a column of 2, then a column of 1; it has 1 in
the top row, 3 in the bottom row; it looks like a
triangle sort of; it looks like a "T".)
- If you had to write a number sentence about this
building, what could you write? (Possible
responses: 1 + 2 + 1 = 4, 1 + 3 = 4, 3 + 1 = 4)
- How many cubes or cubic units are in this building? (4 cubes or 4 cubic units)
- What is the volume of this building? (4 cubic
units)
- Can different shapes have the same volume? (yes)
- Does 1 + 1 + 1 + 1 = 1 + 2 + 1? (yes)
When students finish, encourage the pairs to select
one shape they made and describe it to the class.
Ask them to come up with a number sentence to
describe their shape. Have other students look at
their own shapes and consider whether they made
the same shape as the one being described.
- Did anyone else make the same shape that
[student name] is describing? How do you know it
is the same?
- How many cubes does it have?
- How is it constructed?
- What did [student name] say in the description
that made you think it was the same as yours?
- Can you turn yours so that it looks just like [student
name]'s?
- Would you add anything to the description?
- Can someone else describe [student name]'s
shape?
- Can you name a different number sentence?