Display and direct students' attention to the
Contessa Is Confused Master. Ask students to examine
the building Contessa made and her number sentence.
- Is Contessa's number sentence correct? Why or
why not? (No; Possible responses: You can
change the order in which you add numbers, but
you can't do that in a subtraction problem.
Adding and subtracting the same numbers will
not get the same answers.)
- How can you demonstrate this with cubes?
Students should conclude that the commutative
property applies to addition but not to subtraction.
1 cube plus 3 cubes plus 7 cubes plus 9 cubes does
not give the same result as starting with 9 cubes and
subtracting 7, 3, and 1 cubes.
- Write a correct number sentence about this building. (Possible responses: 7 + 3 + 9 + 1 = 10 + 10;
20 = 7 + 3 + 9 + 1; 10 + 10 = 7 + 3 + 9 + 1;
10 + 7 + 3 = 10 + 10)
- Can you group the numbers in any way that makes
sense to you when adding? Give an example. (Yes; I grouped 7 + 3 to make a ten and 9 + 1 to
make a ten. 10 + 10 = 20.)
Students should conclude that the associative property
of addition allows them to group and add numbers
in ways that make sense to them.
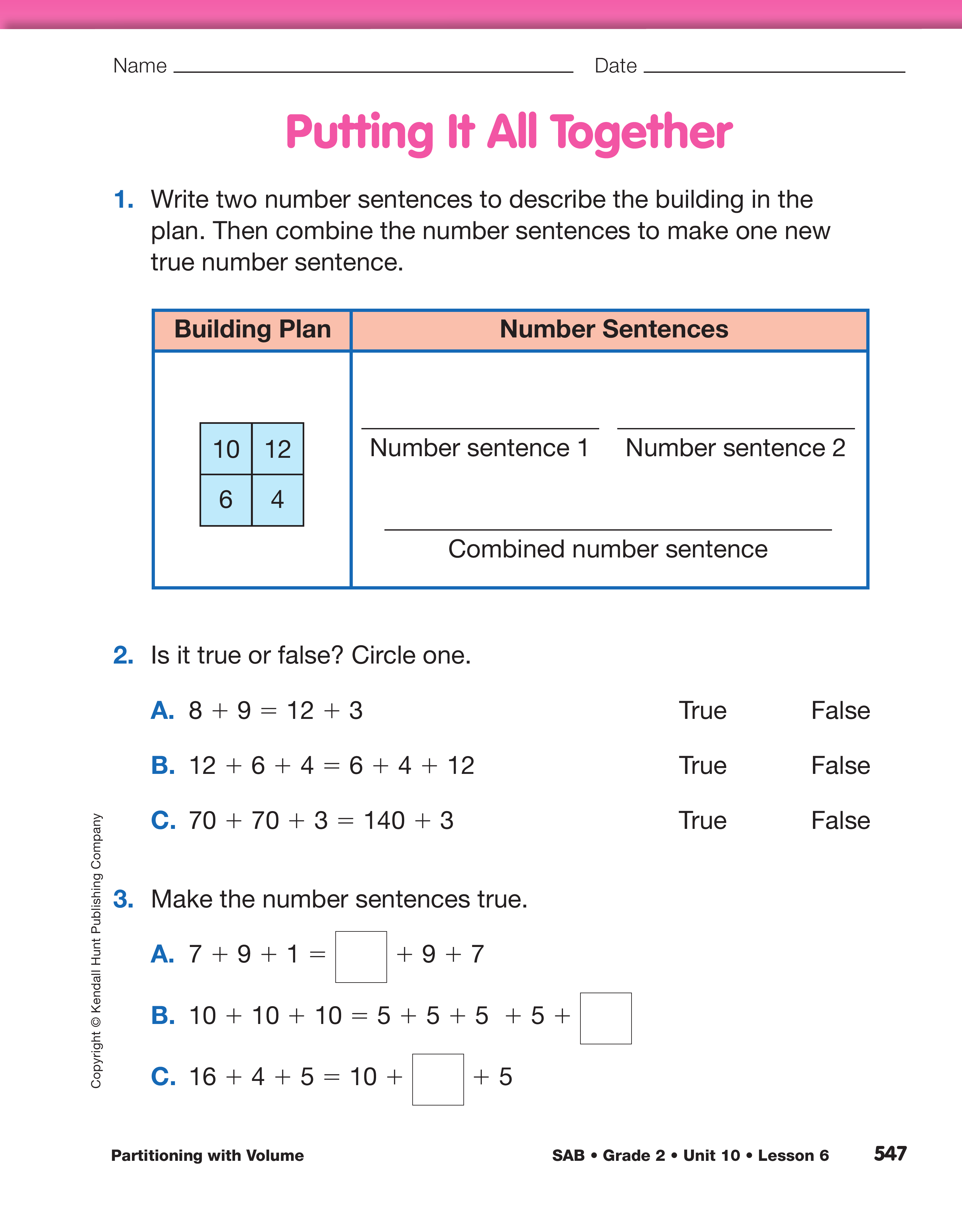
Assign the Putting It All Together page in the
Student Activity Book to assess students' abilities to
describe the volume of buildings using various partitions
of numbers.
Ongoing Assessment
Assign the Putting It All Together page in the Student Activity
Book to assess students' abilities to recognize that different
partitions of a number have the same volume [E1]; solve
addition problems involving volume [E2]; count and add
cubic units to find volume [E8]; and apply the properties of
addition to write number sentences that represent volume [E3].