Buildings and Problems
Est. Class Sessions: 2Developing the Lesson
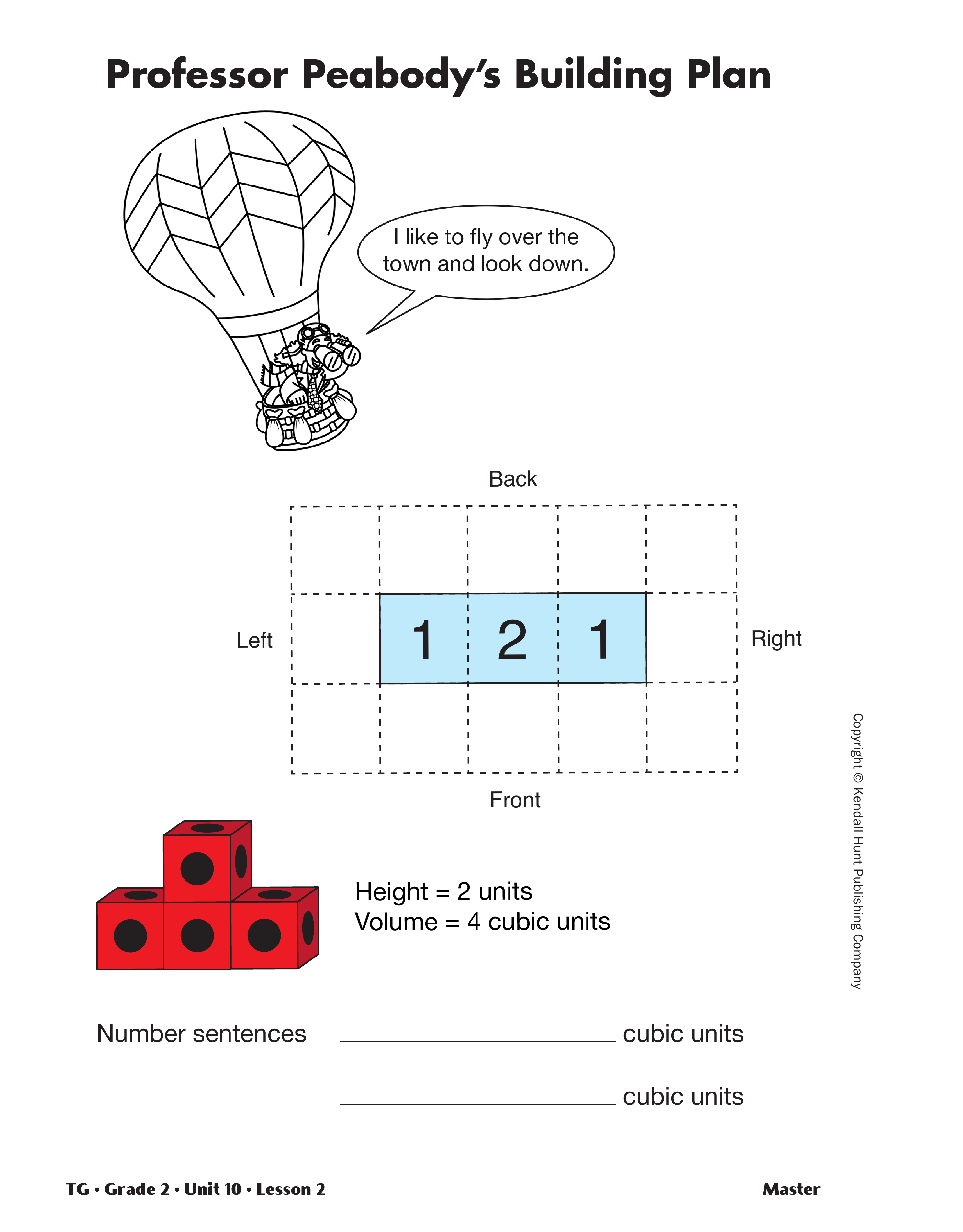
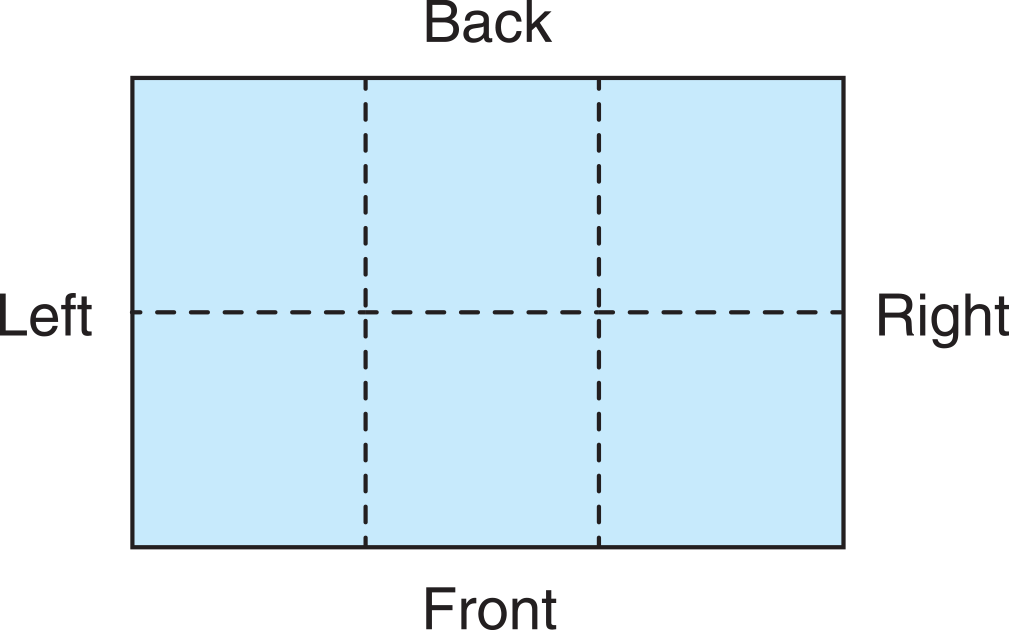
Construct Buildings Given the Floor Plans and the Volumes. Show students the building you prepared prior to the lesson. See Materials Preparation and Figure 1. As a class, make a building plan for this building. First decide what the floor plan, or outline of the first floor, will be. Ask students to tell you what the difference is between a floor plan and a building plan. The building plan indicates the height, while the floor plan does not. The floor plan for this building will be 2 squares long from front to back and 3 squares long from left to right. Draw and shade that outline on a display of the Building Plan Two Ways Master from Lesson 4. See Figure 2.
Now that you have the floor plan for the building, ask:
Remind students that the height of a building is the height of the tallest column. In this case, all the columns are the same height. This is not always the case.
Ask two or three students to come to the front of the room. Ask them to pretend that they are flying over the building.
Ask them to look down on the building.
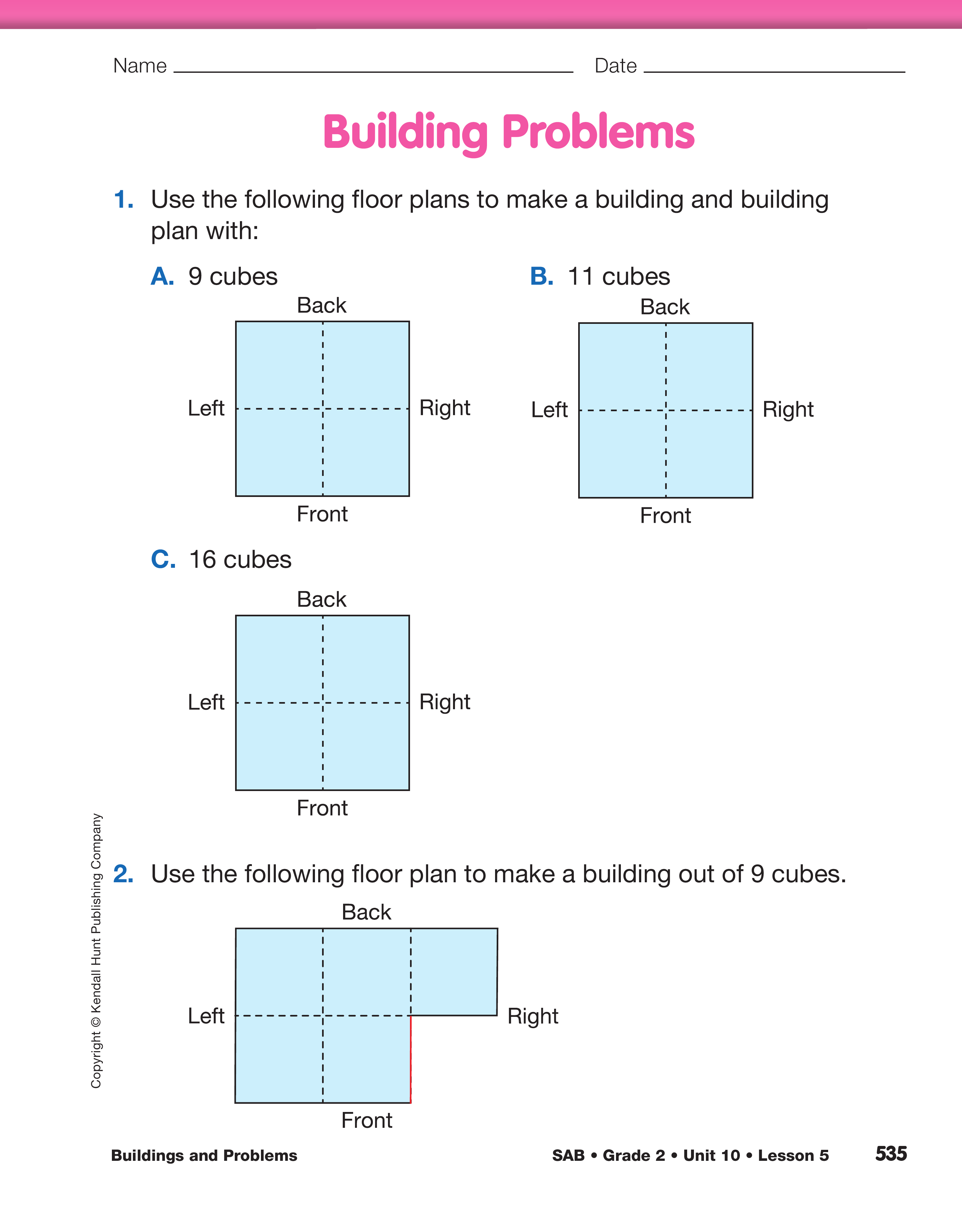
Show a display of the Building Problems page from the Student Activity Book as you discuss the problem in Question 1A:
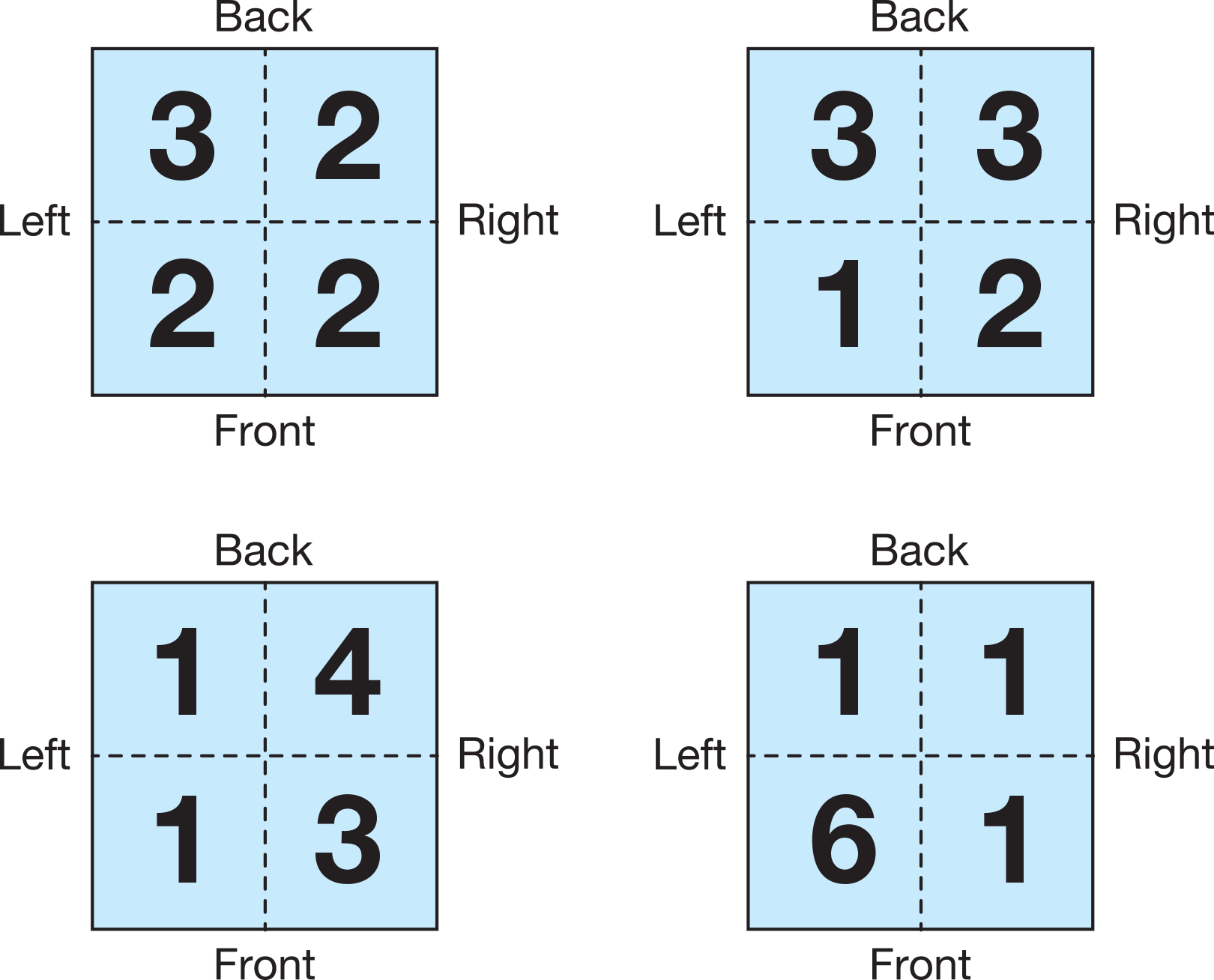
The four squares on the floor plan show the shape of the bottom layer of the building that the students will build. For Question 1A, students' buildings will have a base that is a two-by-two square. Ask student pairs to work on the problem. Question 1A has more than one solution. Some solutions are shown in Figure 3.
Ask students to examine one another's buildings as you pose the following questions:
Ask students to build the tallest and shortest buildings with the 9 cubes.
Have a student show his or her building and draw the corresponding building plan. See Figure 3.
Ask:
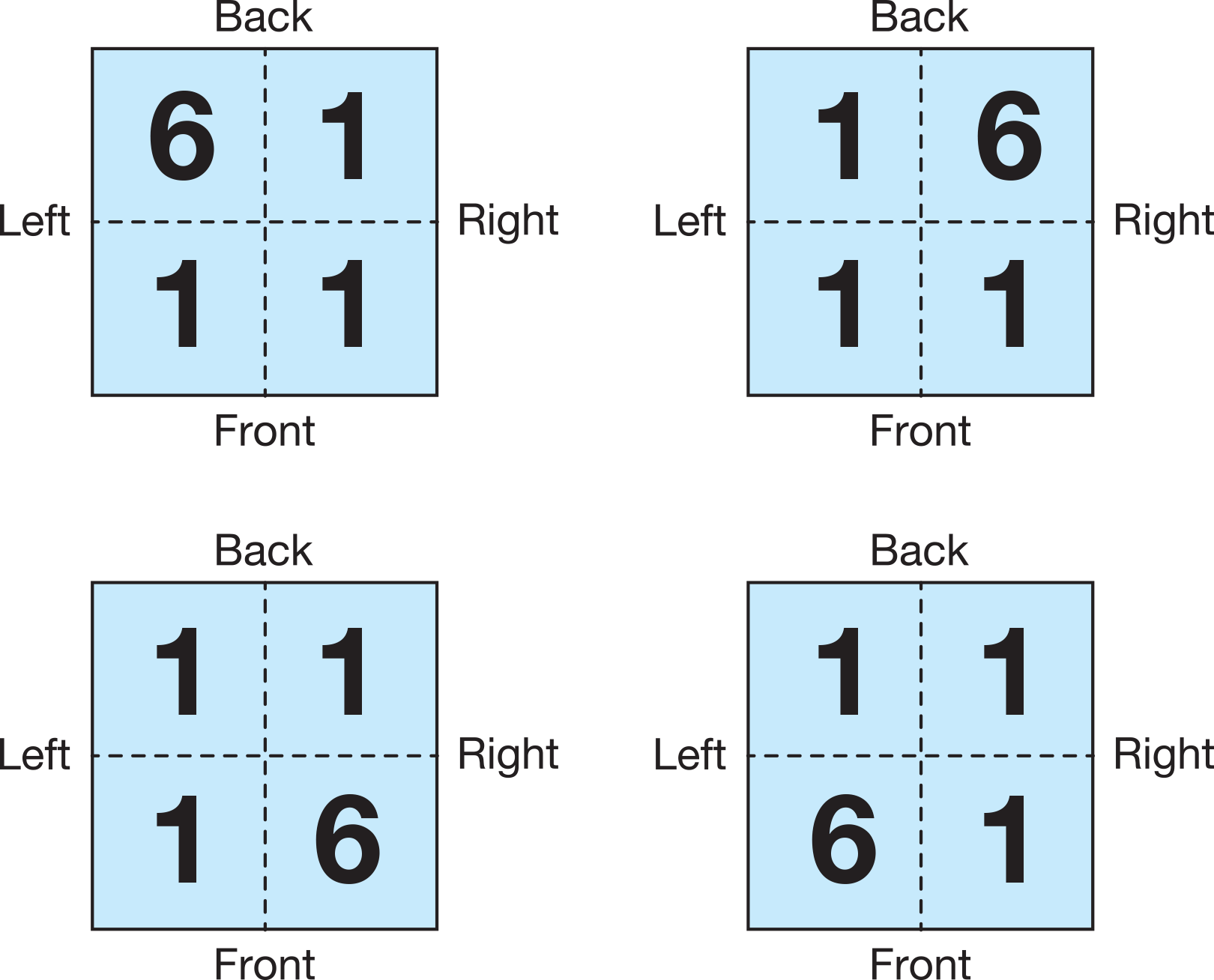
To match the floor plan in Question 1A and use 9 cubes, the tallest building must have a column of six cubes and one cube in each of the other three columns as shown in Figure 4. Students can draw four different floor plans that match the clues. However, the shapes of all four buildings are the same.
Ask:
Have a student show his or her building and draw the corresponding building plan. See the top row of examples in Figure 3.
Ask:
Ask students to complete the remaining problems on the Building Problems page. After each problem, have students analyze the different solutions and share their observations with the class.
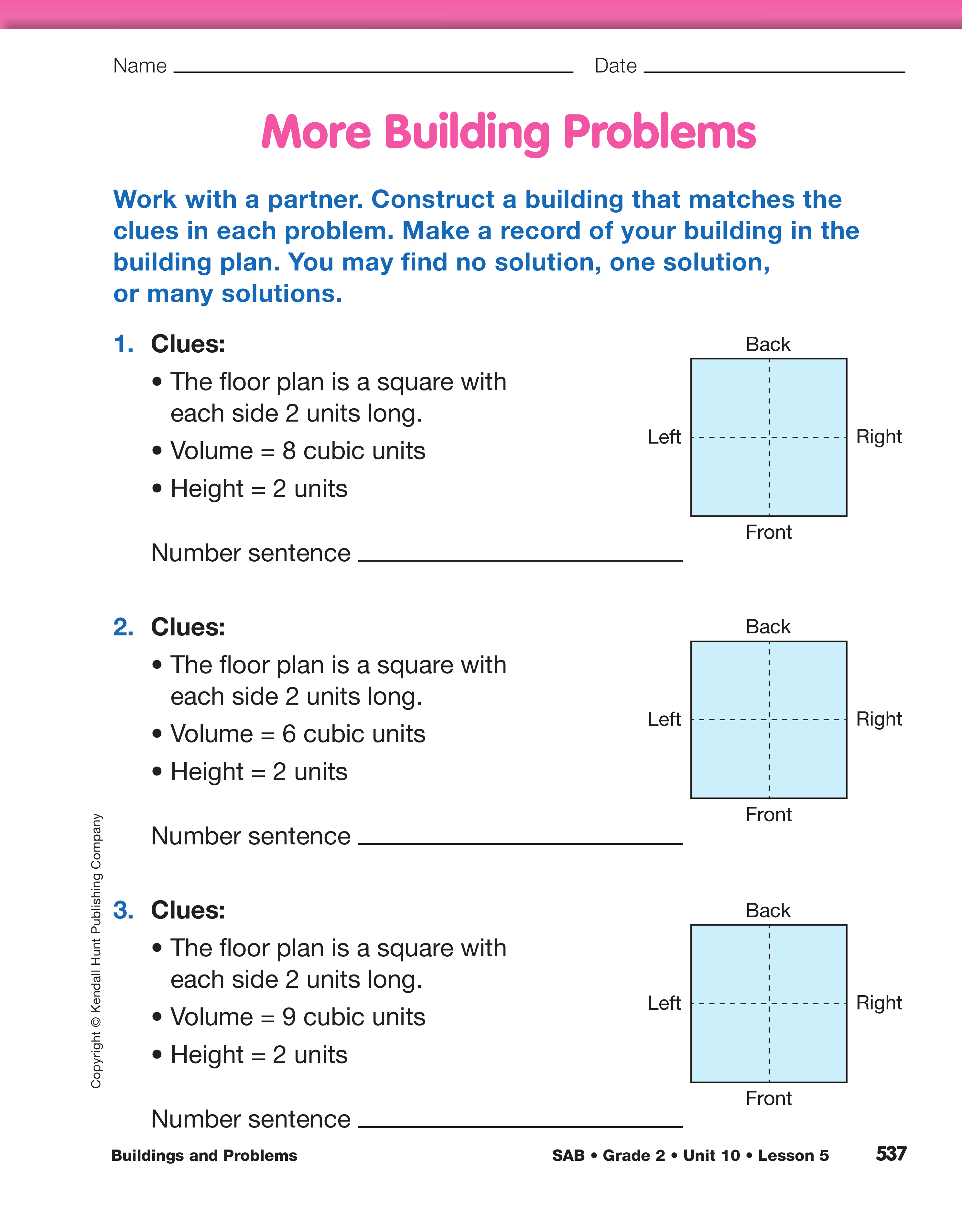
Use Clues to Construct a Building. Remind students of Math Practices Expectation 1, Know the problem. It tells students to read problems carefully so that they know what information is important to solving a problem. In the next set of problems, students are to carefully read a list of clues.
The students will construct buildings based on the following clues:
- the shape of the floor plan
- the volume of the building
- the height of the building
Read the first problem on the More Building Problems pages in the Student Activity Book with the class. The first clue is that the floor plan is a square with each side 2 units long.
Ask:
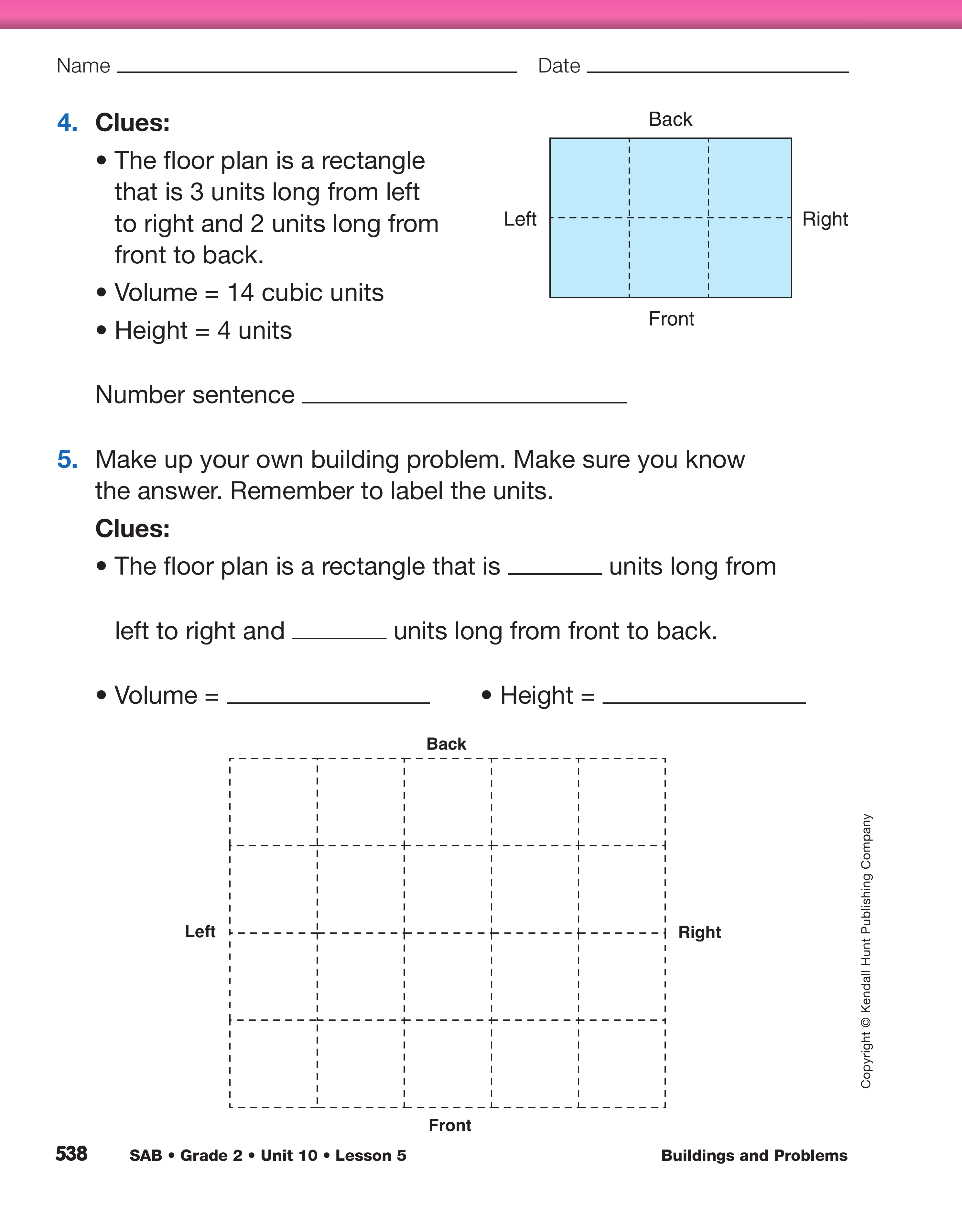
Ask students to construct the buildings in Questions 1–4 and record their work. After they complete their buildings, ask students to compare their work with a neighbor.
Ask:
Students make up their own building problem in Question 5. When students have completed the problems, ask two or three to show their buildings and have the rest of the class construct a building with their clues.
For each, ask: