Buildings and Plans

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Constructing Buildings and Finding Volume

Share Strategies for Finding Volume. Show your model of the Duet Towers that you prepared prior to the lesson to the class. See Materials Preparation. Display the Duet Towers Master as well. Have students describe the building. Remind students to use the correct units when discussing the dimensions of the buildings. When telling the height, width, or length of the building, remind them to add "units" to their answers. When they discuss the volume, remind them to use "cubic units."

For example, ask:

How many stories tall is Duet Towers? (11 stories)
How long is the building from left to right? (2 units)

Point to the third dimension.

How long is the building from front to back? (1 unit)
How could you find the volume of the tower? (Possible response: I could count the cubes.)
Write a number sentence to show how you found the volume of the tower. (Possible response: I grouped the cubes by columns. 11 + 11 = 22 cubic units.)
What do each of the numbers in your number sentence represent? (Possible response: 11 is how tall the building is and there are two towers. There are 11 cubes in one column and 11 cubes in the other column, so there are 22 cubes total.)

Display the number sentences students give to illustrate how they found the volume of the Duet Towers building. Encourage students to look for more than one way to solve this problem. Some might group the cubes by column. Others may group the cubes by rows: 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 22 or 11 x 2 = 22 cubic units.

Ask:

What does each number represent? (There are 2 cubes on a floor, and there are 11 floors so there are 11 twos.)

Discuss students' methods. See Content Note.

This discussion helps point out that the order of the dimensions of the building does not make a difference. Students will apply two important properties of addition as they share their strategies for finding volume in this lesson. The commutative property of addition states that changing the order of addends does not change the sum. As per the commutative property, 4 + 6 + 8 = 8 + 6 + 4.

The other property is the associative property of addition. The associative property states that the addition of a set of numbers, such as those describing the length, width, and height of a cube building, is the same regardless of how the numbers are grouped. For example, (4 + 6) + 8 = 4 + (6 + 8). Students can group and add numbers in ways that make sense to them.

Now turn the Duet Towers building on its side.

Ask:

How many stories tall is the building now? (2 units or 1 unit, depending on how the building is displayed.)
How long is the building from left to right now? (11 units)
How long is the building from front to back now? (1 unit or 2 units, depending on how the building is displayed.)
How many cubic units does it take to construct this building? (22 cubic units)
What is the volume of the building now? (22 cubic units)

Compare the dimensions and volume of the building for both orientations.

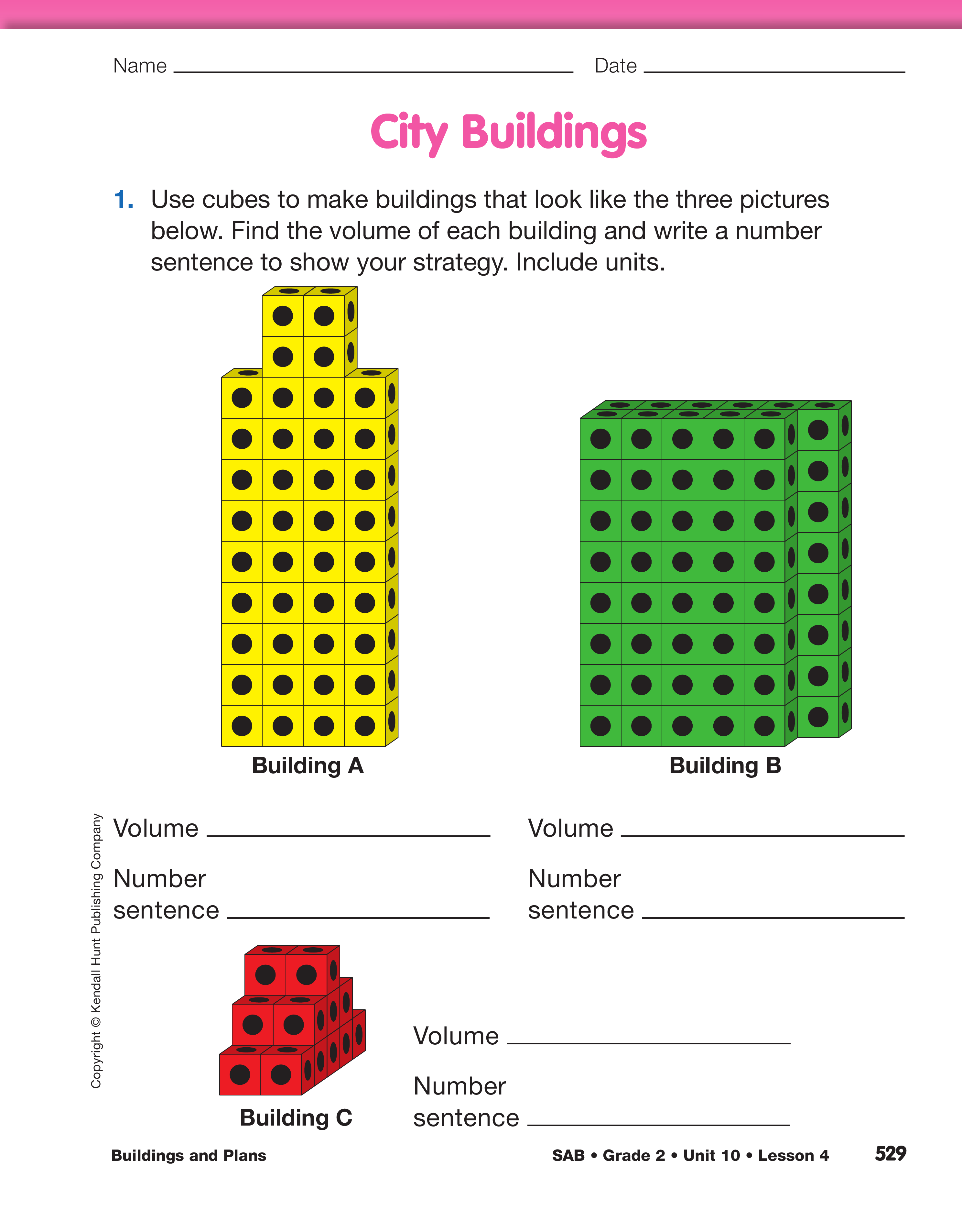
Construct City Building A. Have student pairs create a building that looks like the picture of Building A on the City Buildings page in the Student Activity Book. Students should record the volume of the building and write a number sentence that matches how they calculated the volume. Ask student pairs to share why each number was used and what each of the numbers represents. Students should also discuss how one group's methods were the same or different from another group's methods as they determined the volume of Building A.

Ask:

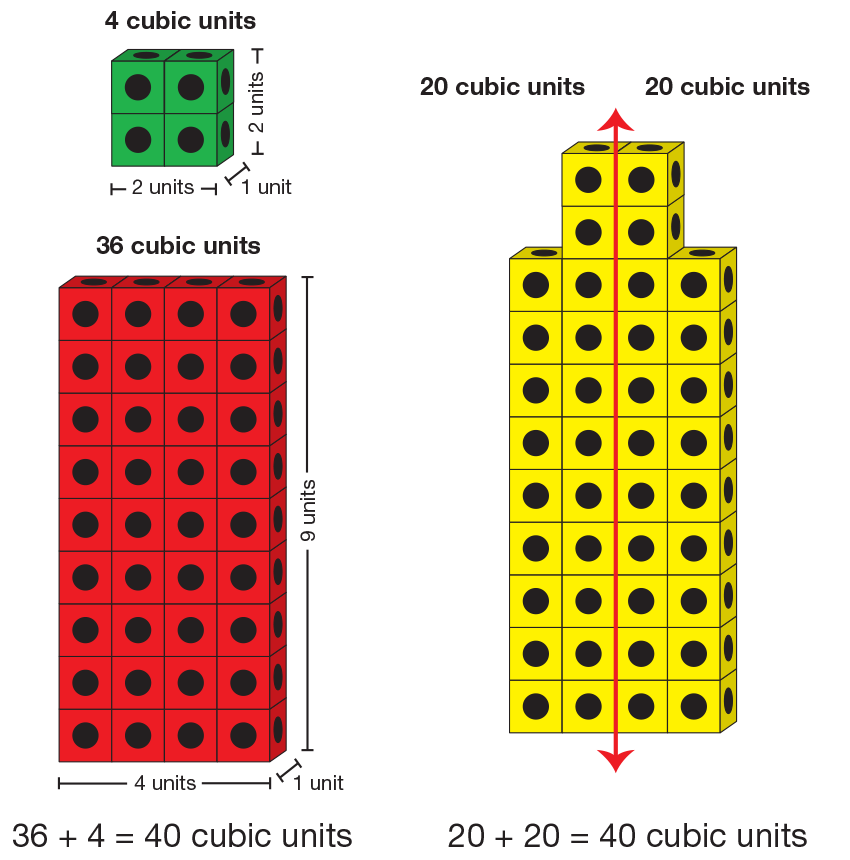
Did anyone break their buildings apart?

One possible strategy is to break Building A into two parts. See Figure 3. One part could be a building that is 4 units long from left to right, 1 unit long from front to back, and 9 units tall. This part would have a volume of 36 cubic units. The other part could be 2 units long from left to right, one unit long from front to back, and 2 units tall. This part would have a volume of 4 cubic units. Together the volume of the building would be 40 cubic units.

Another possible strategy is to use symmetry and divide the building in half lengthwise. One-half of the building has a volume of 9 + 11 = 20 cubic units. Doubling 20 gives 40 cubic units. See Figure 3.

Another strategy involves students moving and grouping Building A's cubes so that the top two cubes are moved down into the "holes" in the row below, making 10 complete rows. 10 rows of 4 cubes is 40 cubes. See Figure 4.

After students share their strategies, ask:

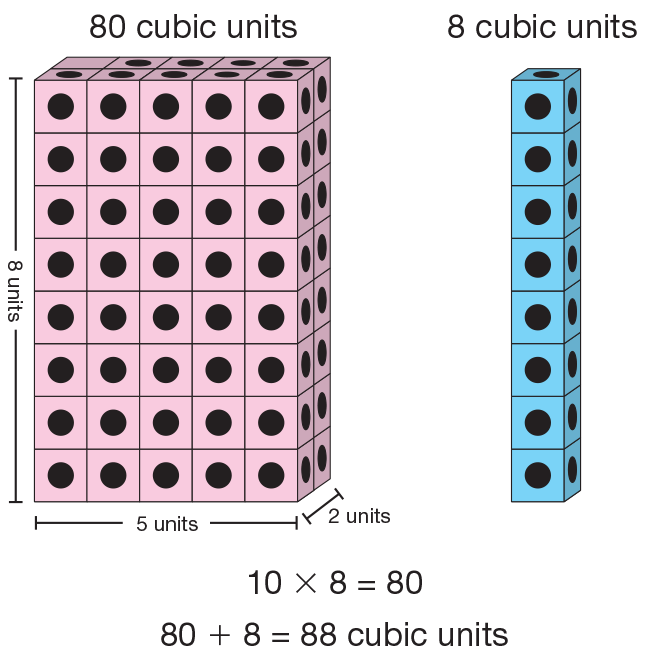
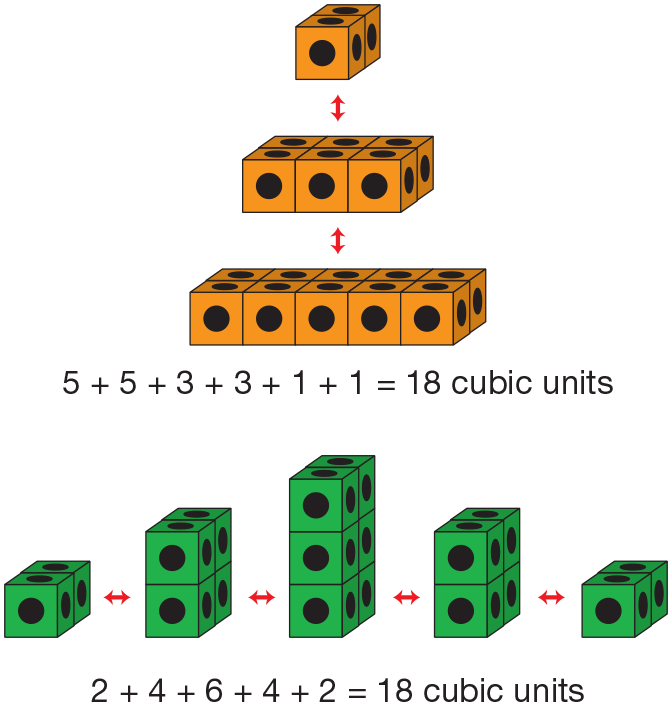
Is one way better than another? Why or why not?

Construct City Buildings B and C. Ask students to construct Buildings B and C and repeat the process and questioning. Figures 5 and 6 illustrate possible strategies for finding the buildings' volumes.

Ask questions similar to the following:

Is one method for finding volume better to use on a given City Building?
Did any students break their buildings apart?
Does that idea work better for Building B than for Building C? Why or why not?
How is one group's method like another group's method? How is it different?

Direct students' attention back to Building C. Figure 6 shows two ways to take apart Building C. Display this number sentence for Building C:

5 + 5 + 3 + 3 + 1 + 1 = 18 cubic units

Then, display this number sentence for Building C:

2 + 4 + 6 + 4 + 2 = 18 cubic units

Ask:

What do the numbers in each of these number sentences represent? (Possible response: the number of cubes in each column of the building; the number of cubes in each layer or floor of the building)
How are these number sentences alike and how are they different? (Both find Building C's volume, but they group and add the cubes differently.)

Both number sentences are correct in that they explain how the students were looking at the building or how they took it apart. The difference lies in the visualization of the building. One pair saw the layers horizontally, so that the two 5s represented the number of cubes on the bottom layer, the two 3s represented the cubes at the middle level, and the two 1s represented the upper layer of the building. The other pair saw the layers vertically, so that the layers are standing up.

Ask:

How did you see (visualize) the building? Compare it with another student pair.

Challenge students to write true number sentences that show that two strategies for finding the volume of a building result in the same volume. See the examples below for Buildings A and C on the City Buildings page. These examples refer to the strategies described in Figure 6. Ask students to match the numbers in the number sentences to the cubes in their buildings.

Building A has a volume of 40 cubic units:
36 + 4 = 20 + 20
Building C has a volume of 18 cubic units:
5 + 5 + 3 + 3 + 1 + 1 = 2 + 4 + 6 + 4 + 2

Adventure Book:

Student Activity Book: 529

Answers