Describe Cube Building Partitions with True
Number Sentences. Display the sample 14-cube
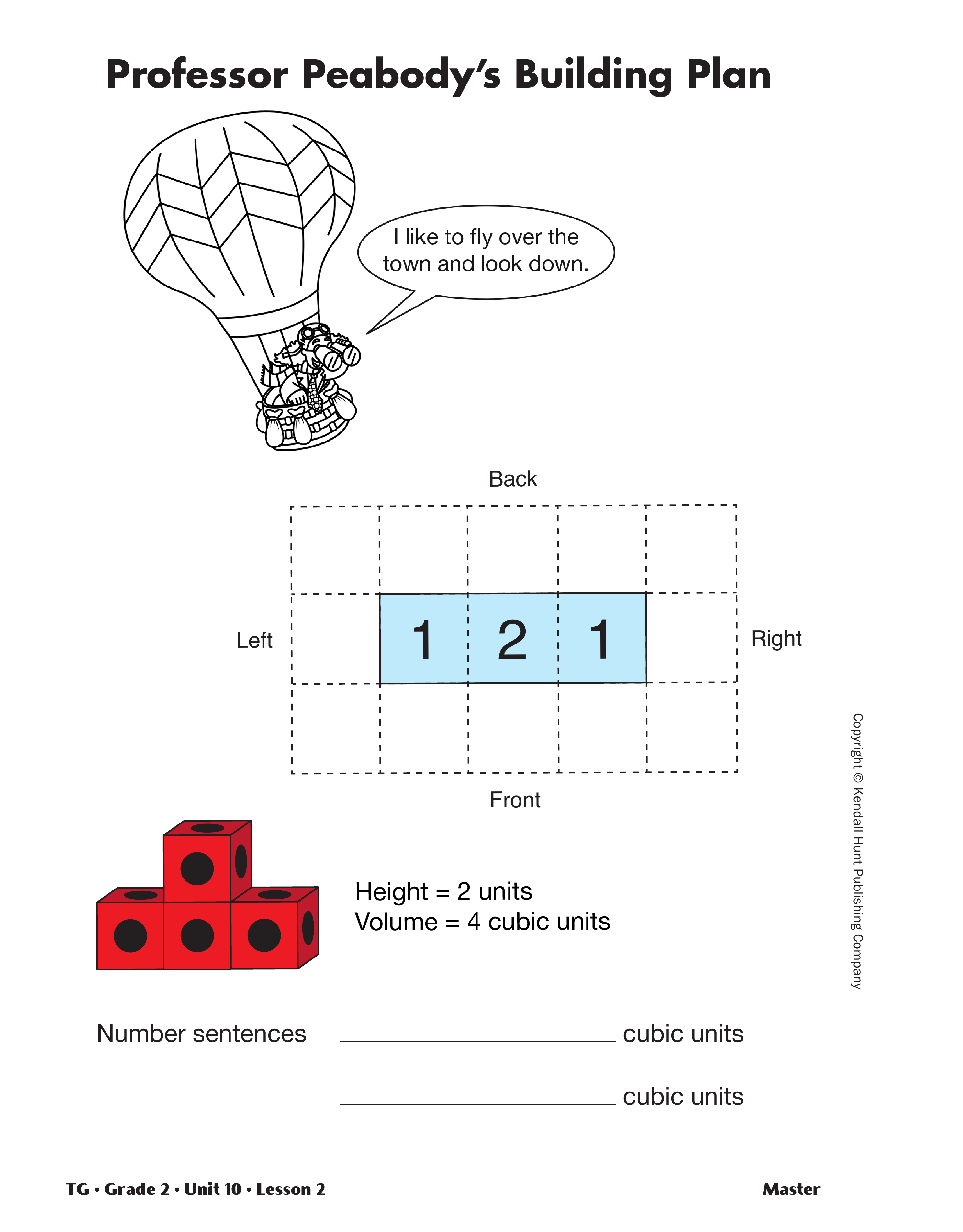
building you prepared prior to the lesson. See
Materials Preparation. Discuss the various ways to
describe the building by columns, looking from left
to right, back to front, by adding the rows, and so on.
Write number sentences to describe the ways to partition
the cubes in the building. Record the related
number sentences.
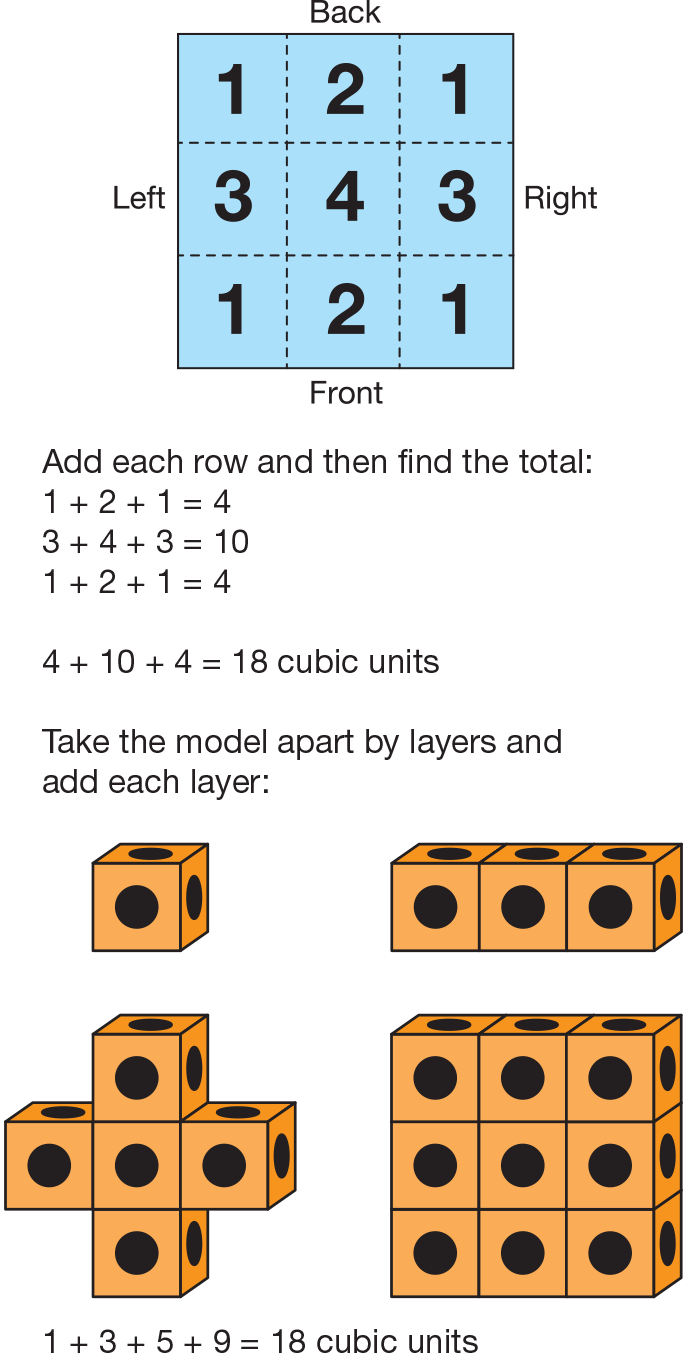
- Can you break this building into columns and
describe it with a number sentence? (2 + 5 + 5 + 2 = 14)
- Can you break this building into rows and
describe it with a number sentence? (4 + 4 + 2 + 2 + 2 = 14)
- How can I combine these two number sentences
into one true number sentence? (2 + 5 + 5 + 2 = 4 + 4 + 2 + 2 + 2)
- How do you group and add these numbers? (Possible response: I add 5 + 5 = 10 and
2 + 2 = 4. 10 + 4 = 14. On the other side of the
equal sign, I double 4 to get 8 and then count on
by 2s: 10, 12, 14.)
- Did anyone group and add the numbers differently?
How?
- Does the order in which you add the numbers matter?
How do you know? (The order doesn't matter
because I can add the same numbers in a different
order and I get the same total.)
- How do you know this is a true statement? (Possible response: Both sides equal 14. Both of
the sentences describe the 14 cubes.)
- What does the equal sign in this number sentence
tell you? (The quantity shown on one side of the
equal sign is the same as the quantity shown on
the other side of the equal sign.)
See the Content Note for more about the equal sign.
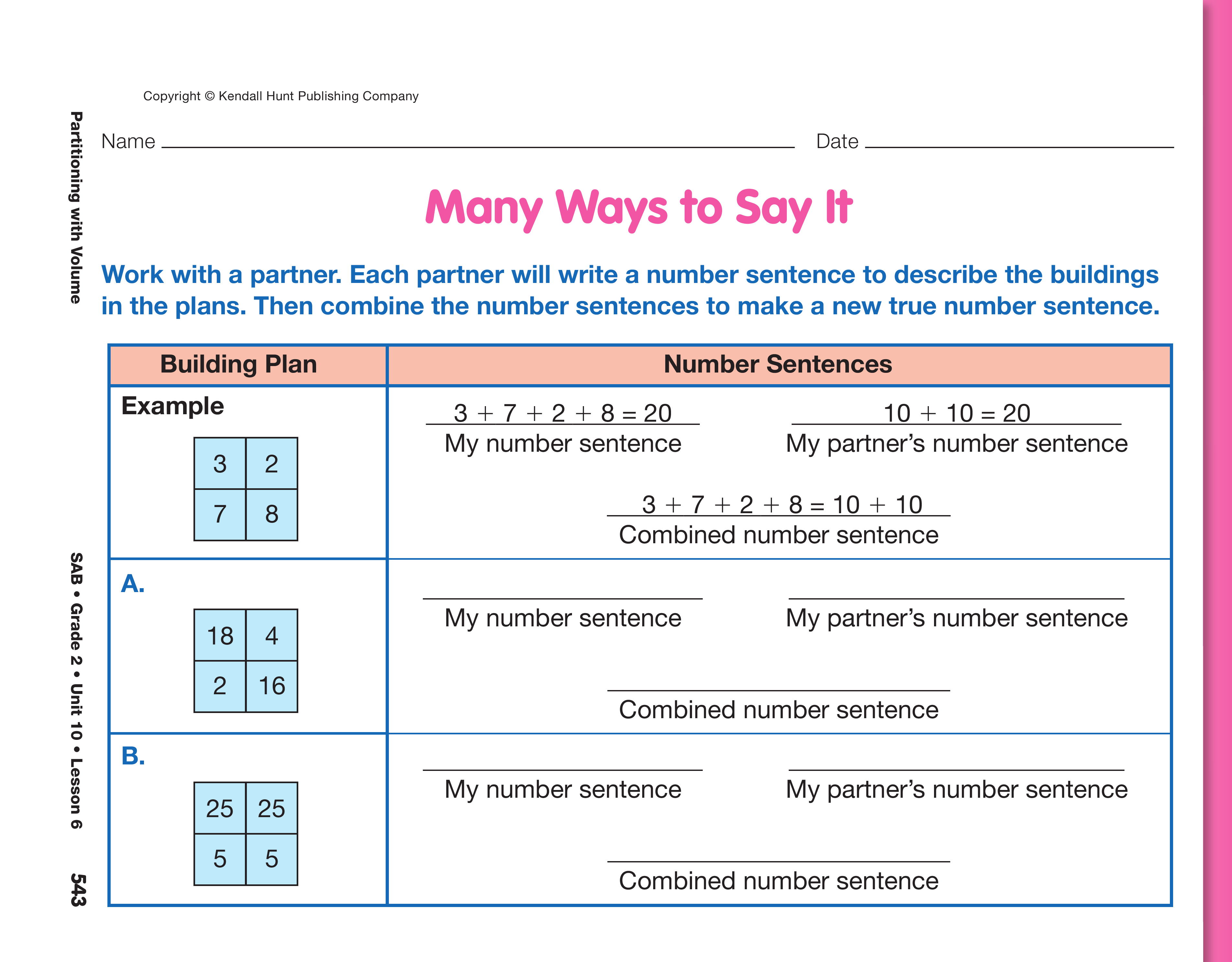
Display and direct students to the Many Ways to Say
It pages in the Student Activity Book. Students will
work in pairs for Questions A–E. For each question,
students will look at the building plan. They will
each write a different number sentence to describe
the building. Then they will combine the two number
sentences to make a true statement with more
than one addend on either side of the equal sign.
Students may refer to their desk number lines and
the 200 Chart in the Student Activity Book Reference
section. Before students begin working, discuss the
example on the page.

The equal sign (=) is one of the most important signs in
mathematics, yet many students struggle with it
conceptually. It is vital that students understand that the
equal sign does not mean, "the answer is coming up next,"
but instead means, "is the same as." When you are working
on these equations with the students, make an effort to use
the language "is the same as" when reading the equal sign.
When students have completed Questions A–E, ask:
- How did you group and add the numbers in
Question A? (Possible response: 18 + 2 = 20 and
14 + 6 = 20. 20 + 20 = 40.)
- Did anyone group and add the numbers differently?
Did you get the same answer? (yes)
- Look at Question B. Do you see an easy addition
problem? (Possible responses: 25 + 5 = 30.
30 two times is 60. Or, 25 + 25 = 50 and
5 + 5 = 10. 50 + 10 = 60.)
- Show us your building from the building plan in
Question E.
- What two number sentences describe your building?
Show how the numbers in the sentence
match with the cubes in your building.
Write the number sentences on the board. Combine
the two number sentences to make one new true
statement. Display the combined number sentence.
- Is this a true number sentence? How do you
know? (Yes, it is true. I know because you can
see that one side of the equal sign shows [number]
cubes and so does the number sentence on
the other side.)
- Show how you group and add the numbers.
- Does it matter how many addends there are on
each side of the equal sign? (No; You can break a
number down any way you like.)
True or False Statements. Assign the True or False
page in the Student Activity Book to give
students more practice looking at different partitions
of a number connected by an equal sign.
- How did you decide if a statement was true or
false? (Possible response: I added the numbers
on each side to see if they made the same total.)
- How did you group and add the numbers in
Question [B]?
- Why is Question D true? (You can add the numbers
in any order. 6 + 14 is the same as 14 + 6.)
- Why isn't Question E true? (Adding 6 + 4 is not
the same as subtracting 4 − 6.)
- In Question G, does 50 + 30 + 2 = 2 + 30 + 50?
Does it matter in what order you add the numbers?
Show us. (Yes, this is a true number sentence.
The order in which you add the numbers doesn't
matter. 50 + 30 + 2 equals 82 and 2 + 30 + 50
also equals 82.)
- What strategies did you use to figure out the missing
number in Question 2A, 6 + 7 = 7 + ? (Possible response: I know both sides of the
equal sign have to show the same amount. I
already had 7 on each side, so I needed a 6 on
both sides.)