Ask students to read the instructions on the Building
Detective pages in the Student Activity Book. It is
important that each student knows what is being
asked in order to construct Romesh's building.
Display the Math Practices page from the Student
Activity Book Reference section. Direct students'
attention to MPE1, Know the problem.
- Did you read the question carefully? Do you
know what to do in order to complete Questions 1
and 2?
Students need to recognize that they have to interpret
Romesh's number sentence so that they can draw a
building plan for his building, construct his building,
construct their own building with the same volume,
make a plan for their building, and write number
sentences.
To complete the task, students need to know what is
being asked and expected of them:
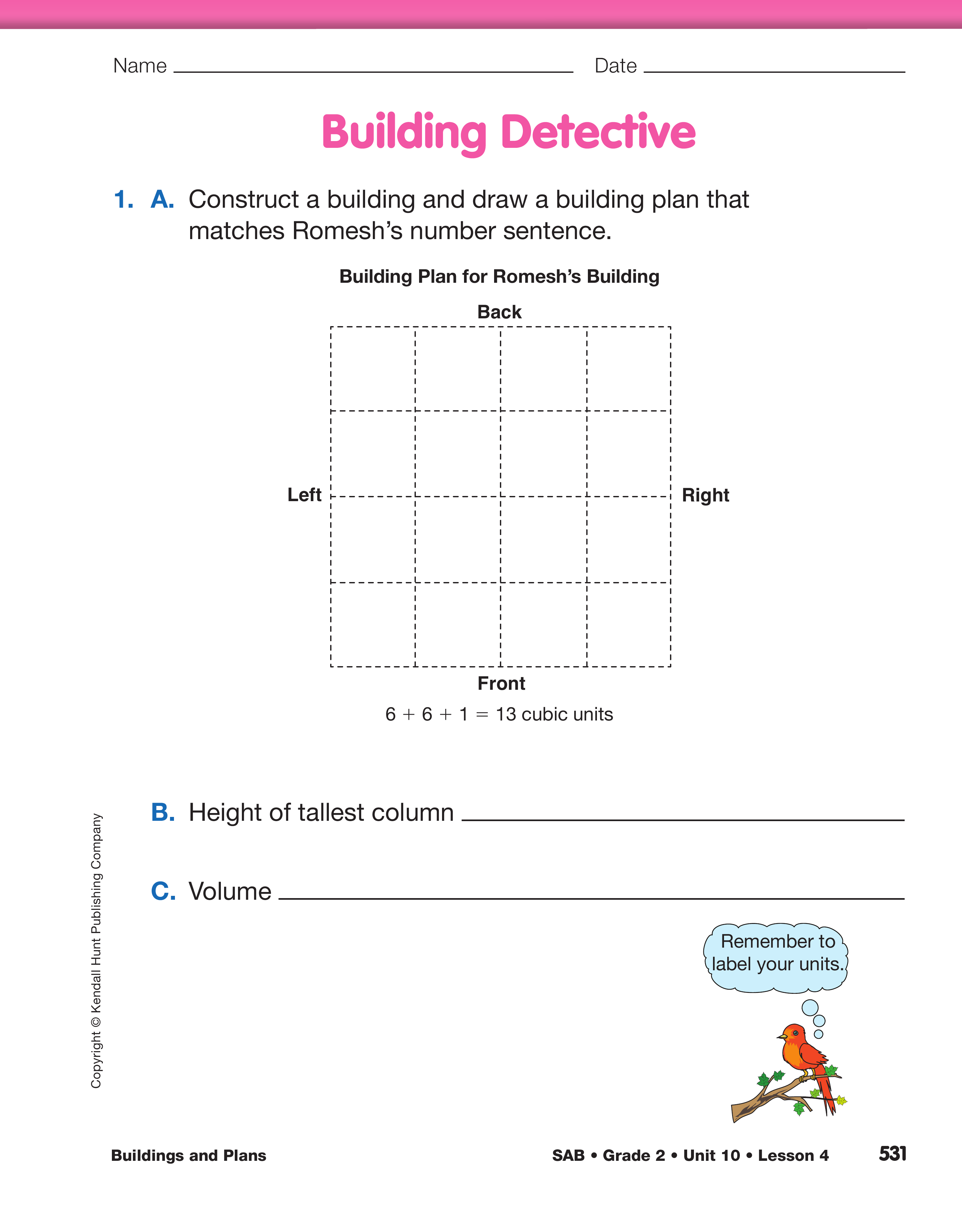
- The number sentence that Romesh gave for his
building is 6 + 6 + 1 = 13 cubic units.
- Draw a building plan of Romesh's building.
- Construct Romesh's building.
- Construct a different building with the same volume
as Romesh's building.
- Make a building plan of the new building.
- Write a number sentence that shows a way to
find the volume for the new building.
Next, focus students' attention on MPE5, Show my
work, and MPE6, Use labels.
- How can you show or tell how you solved the
problem so someone can see why your strategy
makes sense? (Someone else should be able to
point out the cubes in the building I built for
Romesh that match the building plan and the
numbers in Romesh's number sentence. Another
person should be able to match the cubes in my
building to my building plan and number sentence.)
- What labels should you include to show what the
numbers mean? (volume in cubic units and
height in units)
Students should work in groups of two to four to
solve the problem. Work can be displayed around the
room so that comparisons can be made between each
group's constructions.
Some points to consider are:
- How many different ways was Romesh's building
constructed? How are they the same? How are
they different?
- How many different buildings with a volume of
13 cubic units were constructed? How are they the
same? How are they different?
- Can different shapes have the same volume? How
do you know? (Yes, we have lots of different
buildings and they all have a volume of 13 cubic
units.)

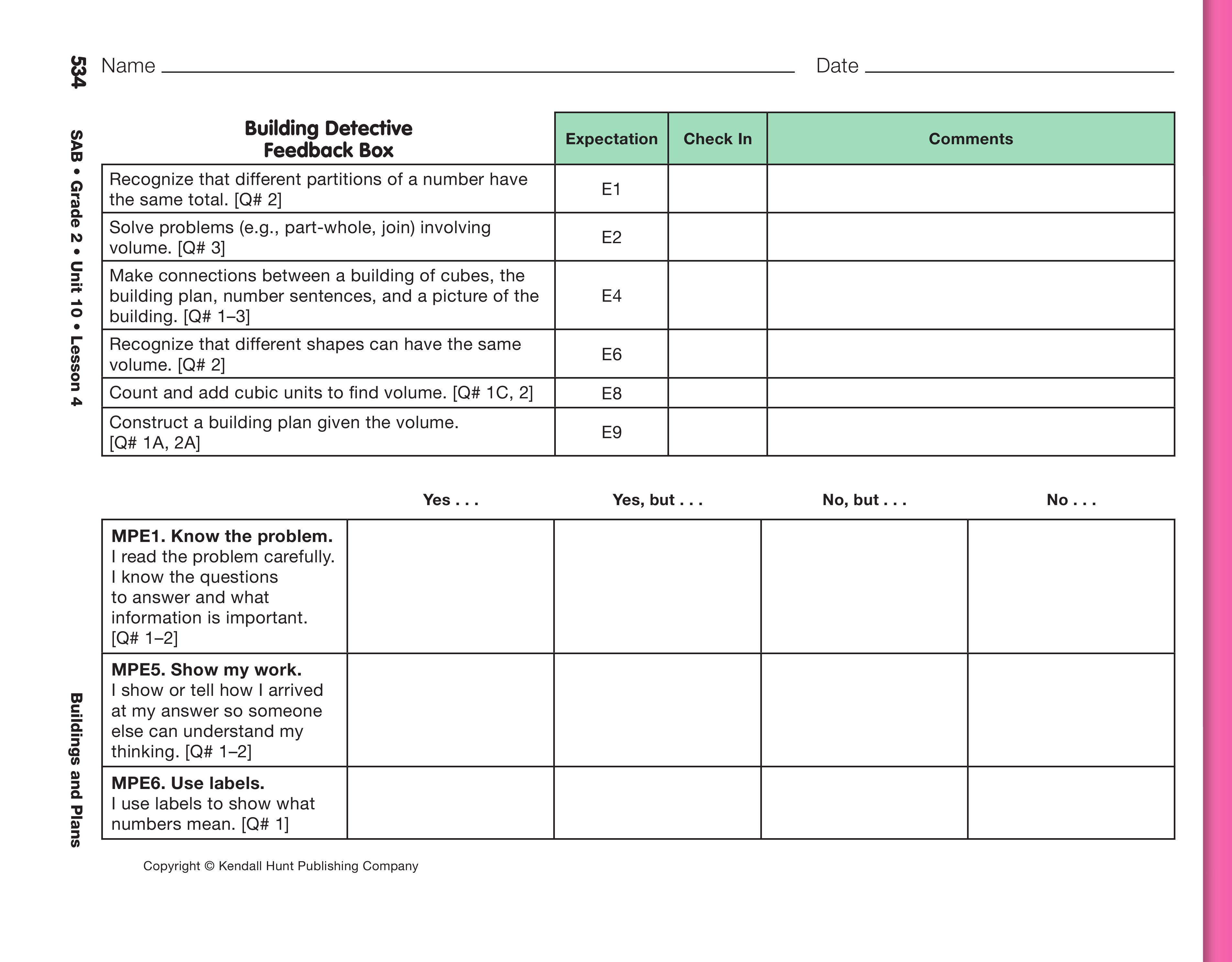
Use the Building Detective pages with the Feedback Box in
the Student Activity Book to assess students' abilities to
recognize that different partitions of a number have the same
total [E1]; solve problems involving volume [E2]; make
connections between a building of cubes, the building plan, a
picture of the building, and number sentences [E4];
recognize that different shapes can have the same volume
[E6]; count and add cubic units to find volume [E8];
construct a building plan given the volume [E9]; know the
problem [MPE1]; show work [MPE5]; and use labels [MPE6].
Place the Building Plan Two Ways Master and connecting
cubes in a center. Challenge students to build a tower or
building and find at least two different ways to partition and
represent volume.