Lesson 3

Architects in Cubeland

Est. Class Sessions: 1–2
X

Mathematical Standards

2.NBT.A
Understand place value. (2.NBT.A.2)
2.NBT.B
Use place value understanding and properties of operations to add and subtract. (2.NBT.B.5, 2.NBT.B.7, 2.NBT.B.9)
2.G.A
Reason with shapes and their attributes. (2.G.A.1, 2.G.A.2)
2.OA.A
Represent and solve problems involving addition and subtraction. (2.OA.A.1)
2.OA.C
Work with equal groups of objects to gain foundations for multiplication. (2.OA.C.4)

Standards for Mathematical Practice

MP1.
Make sense of problems and persevere in solving them.
MP2.
Reason quantitatively.
MP4.
Model with mathematics.
MP5.
Use appropriate tools strategically.
MP6.
Attend to precision.
MP7.
Look for and make use of structure.
MP8.
Look for and express regularity in repeated reasoning.

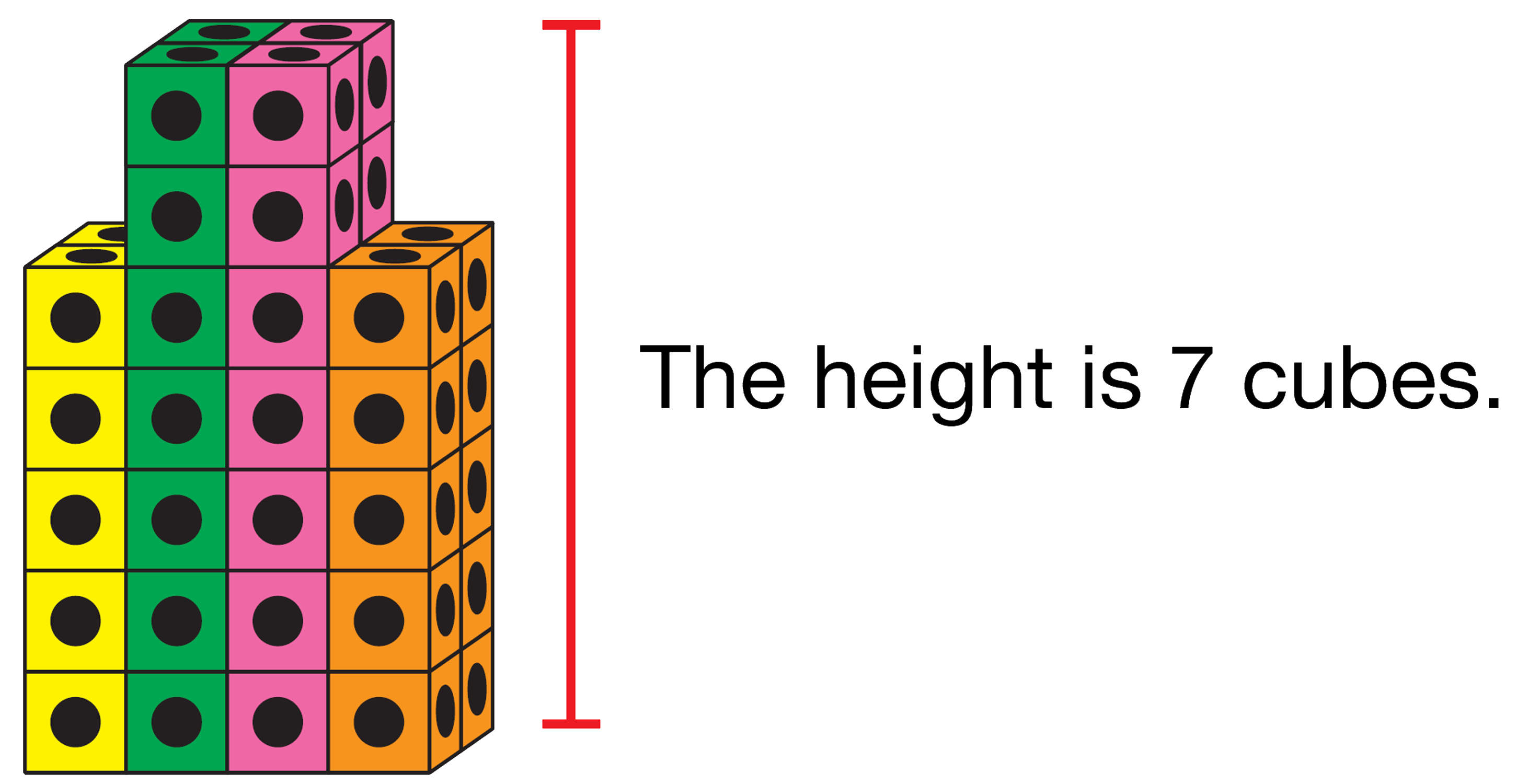
Students pretend to be teams of architects who work in Cubeland. Each team designs and constructs a building, records the design on a building plan, and writes number sentences to fit their building plan. Architect teams exchange plans and construct copies of one another's buildings.

Content in this Lesson

  • Constructing a building plan given the volume [E9].
  • Making connections between a building of cubes, the building plan, and number sentences [E4].
  • Measuring the dimensions (height, length, width) of a building [E7].
  • Counting and adding cubic units to find volume [E8].
  • Applying the properties of addition (e.g., commutative, associative) to write number sentences that represent the volume of a building [E3].
  • Solving problems (e.g., part-whole, join) involving volume [E2].
  • Recognizing that different shapes can have the same volume [E1, E6].
  • Showing work so that others can understand the thinking [MPE5].
  • Using labels to show what numbers mean [MPE6].

Daily Practice and Problems G–H

G. Time

H. Subtraction

X

Materials for Students

Daily Practice and Problems Lesson Homework Assessment

Student Books

 Student Activity Book

Teacher Resources

 Teacher Guide - digital

Supplies for Student Pairs

about 60 connecting cubes

Materials for the Teacher

Display of Rules for Building Plans Master from Lesson 2 (Teacher Guide)
Display of Memo in Architects in Cubeland pages (Student Activity Book) Page 521
Display of Architects in Cubeland Student-to-Student Checklist page (Student Activity Book) Page 523
Display of Missing Columns Master (Teacher Guide)
Unit 10 Assessment Record
3 sample cube buildings for Rules for Building Plans from Lesson 2
connecting cubes, optional

Materials Preparation

Prepare a Learning Center for Optional Targeted Practice. Make copies of the Building Plan section of the Architects in Cubeland pages from the Student Activity Book. Place them in a learning center with connecting cubes. Challenge students to find different ways to represent the volume of the building.

Assessment in this Lesson

Assessment Expectation Assessed Math Practices Expectation Assessed
Architects in Cubeland
with Feedback Box
Student Activity Book
Pages 519–522
and
Architects in Cubeland Student-to-Student Checklist
Student Activity Book
Page 523
E4. 
Make connections between a building of cubes, the building plan, and number sentences.
E7. 
Identify and measure the dimensions (floor plan, height) of a building.
E8. 
Count and add cubic units to find volume.
E9. 
Construct a building plan given the volume (number of cubes), floor plan, and height.
MPE5. 
Show my work. I show or tell how I arrived at my answer so someone else can understand my thinking.
MPE6. 
Use labels. I use labels to show what numbers mean.
What Is the Volume
with Feedback Box
Student Activity Book
Pages 525–527
E1. 
Recognize that different partitions of a number have the same total.
E2. 
Solve problems (e.g., part-whole, join) involving volume.
E3. 
Apply the properties of addition (e.g., commutative, associative) to write number sentences that represent the volume of a building.
E6. 
Recognize that different shapes can have the same volume.
E8. 
Count and add cubic units to find volume.
MPE5. 
Show my work. I show or tell how I arrived at my answer so someone else can understand my thinking.