Make Building Plans. Introduce students to the
imaginary world of Cubeland—a place where all the
buildings are made of cubes. Help students "see" the
buildings from an aerial perspective. Tell them to
pretend they are flying above Cubeland.
- What will the buildings look like when you look
down at them? (lots of squares)
Guide students to visualize that from this bird's-eye
view, each cube looks like a square. Show students
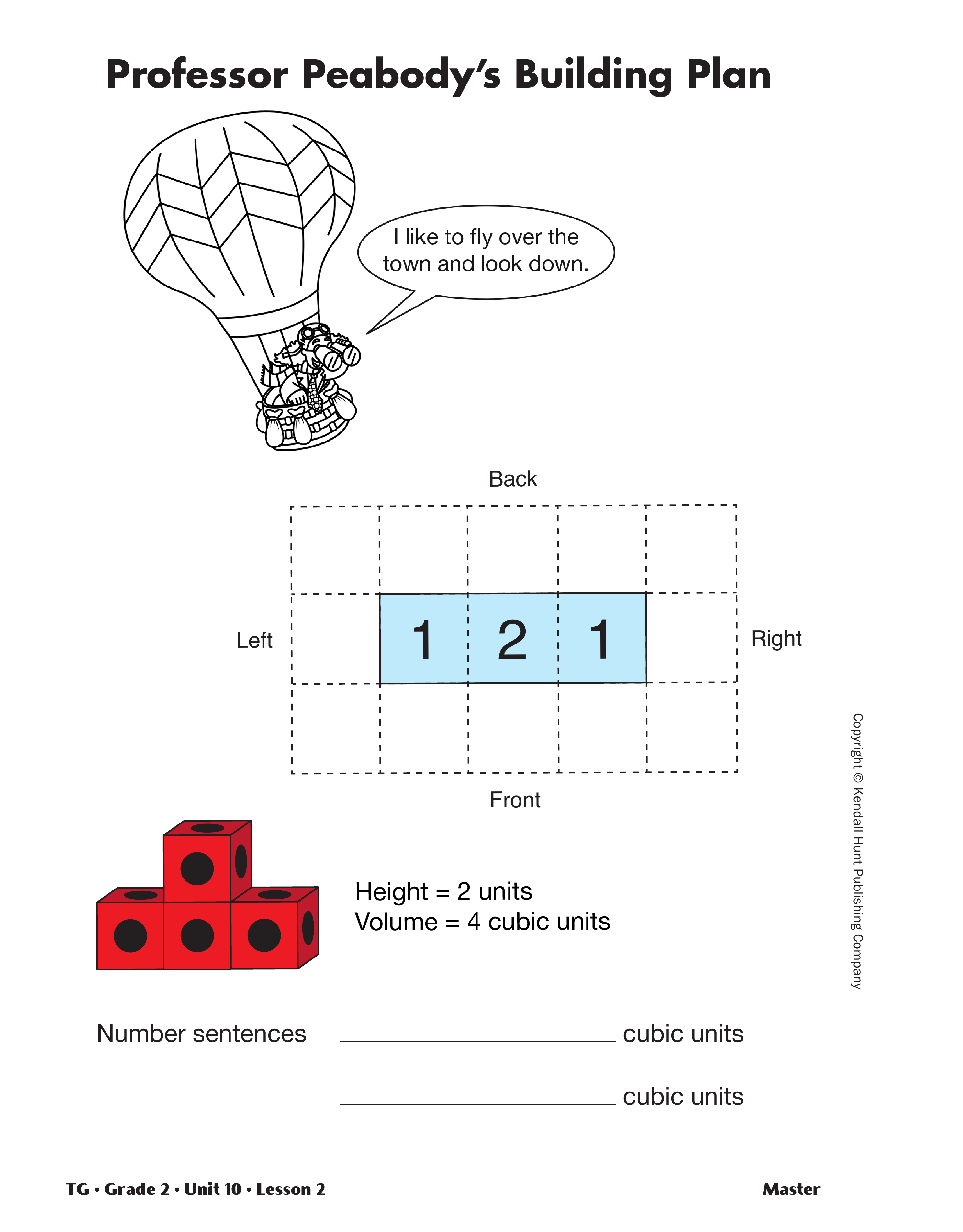
the Professor Peabody's Building Plan Master. Tell
the following story:
- Professor Peabody flew over Cubeland and made
a map of a building he saw. He called the map a
building plan. He recorded the number of cubes
used in each column of a three-column building.
Notice that the middle column is two cubes high
while each of the side columns is one cube high.
Build the building Professor Peabody saw.
- What number sentences could describe the building
Professor Peabody saw? Be sure to explain
how the numbers in your sentence match the
cubes. (If I count by columns, 1 + 2 + 1 = 4. If I
count by rows, 3 + 1 = 4.)
- Look at the measurements of the building. What is
the height? (2 units)
- How are the units for the height, a length, different
from the units for the volume? (The unit for
height is just units and the unit for volume is
cubic units.)
Remind students that volume is the amount of space
something takes up. Volume is measured in cubic
units. Height is a length and is measured with linear
units.
Use Professor Peabody's building plan to introduce
the method that students will use to create and
record the buildings they make.
Encourage students to discuss the fact that architects,
construction workers, and builders work from a drawing
or a blueprint. Students will, like Professor
Peabody, use a special kind of blueprint we call a
building plan.
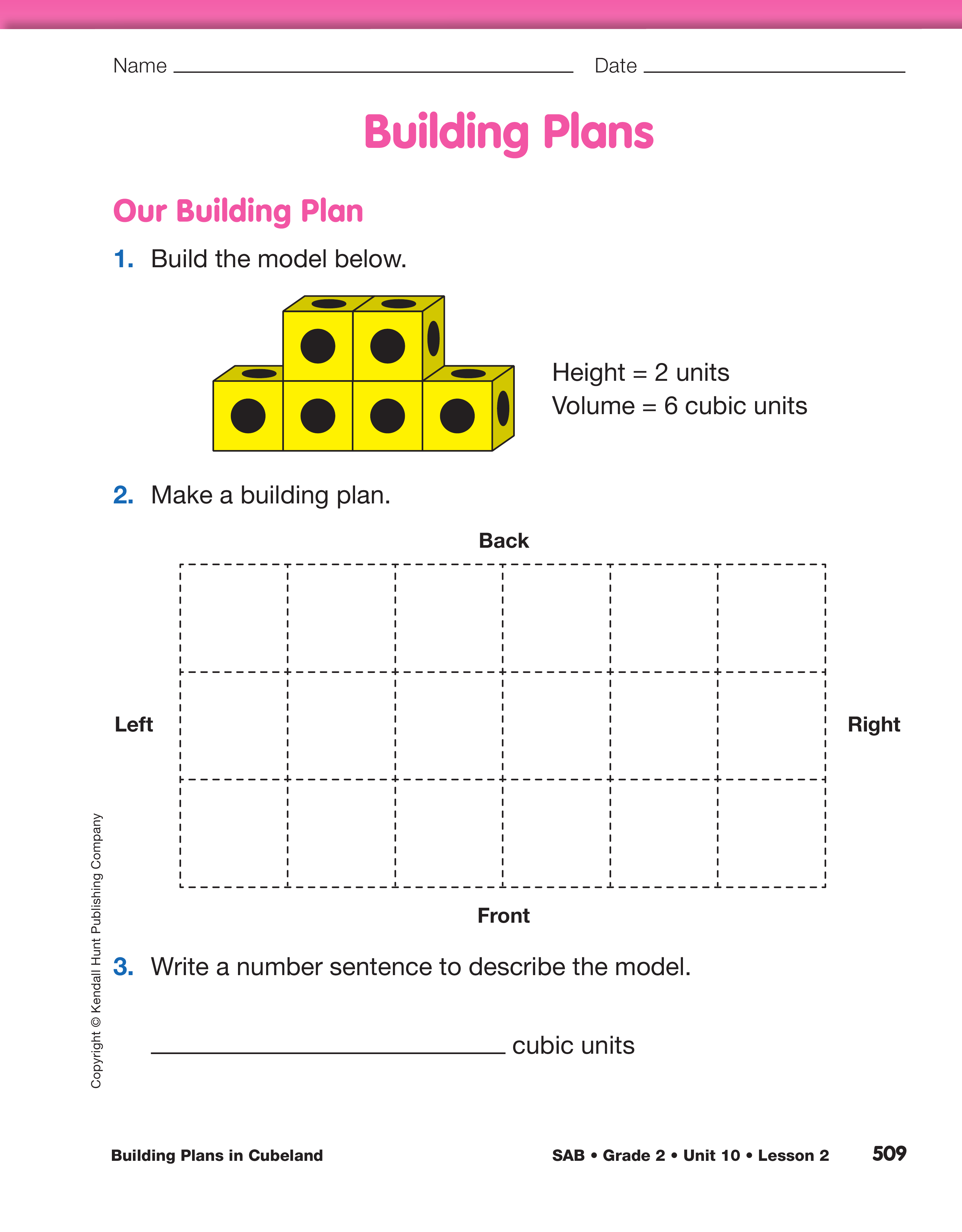
Display the Our Building Plan section of the Building
Plans pages in the Student Activity Book. Ask students
to look at their page and make the building shown in
Question 1. Place the building you prepared from
Figure 1 on the grid and encourage students to imagine
they are looking down at the structure from above. For
Question 2, demonstrate how students can trace the
bottom outline of their buildings onto the grid. Ask
student volunteers to count the number of cubes in
each column and then tell you what the numbers on
the plan should be. Students should then record the
height of each column on their plans. See Figure 5.
- What number sentences describe this building
(Question 3)? (One possible response: I looked at
each row: 4 + 2 = 6.)
- How do the numbers in the number sentence match
with the cubes in the model? (There is one row on
the bottom of 4 cubes and one row of 2 cubes on
the top. There are 6 cubes total.)
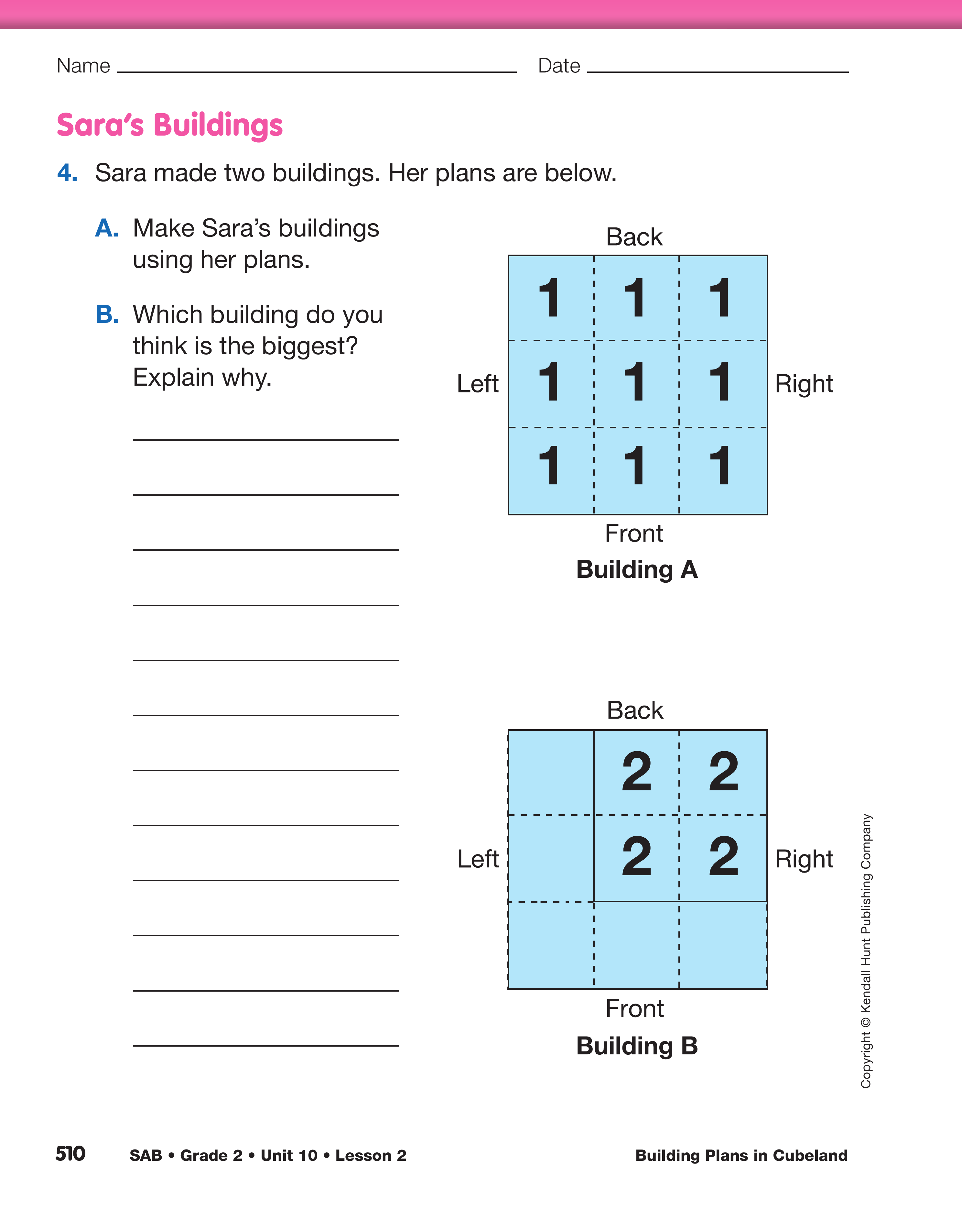
Decide which Building Is Bigger. Students are now
prepared to construct their own buildings. Ask them
to make the two buildings on the Sara's Building
section of the Building Plans pages. Question 4B
may elicit several different answers. Point out that
biggest can mean several different things. See the
Sample Dialog.

The following is a dialog discussing the volume of Sara's
building.
Teacher: How many thought Building B was the biggest?
Can you tell me why, Shannon?
Shannon: Its height is two.
Teacher: Its height is two units, so that makes it bigger.
Because she thinks bigger is taller.
Luis: So do I. I agree. Because it is two, but A has more. But A
is thinner, but B is less, but it is thicker.
Teacher: So you think when maybe we talk about something
being bigger, we say it is either taller, or wider, or it
has more … volume?
Jacob: I don't agree with Luis. He's only thinking of taller, he's
not thinking of wider or anything else.
Teacher: But how do you know what bigger means? If I
asked you what is the biggest building in downtown
Chicago, what would you say to me?
Jacob: The Willis Tower.
Teacher: You're telling me what building is the tallest building.
So how do you know it is bigger? So do you think
maybe Luis has a point? Or, maybe bigger could be
tallest.
Jacob: Remember what we did with the marshmallows and
that lab we did? Luis's not thinking about how wide it is.
Luis: Yes I am.
Teacher: So instead of saying biggest, Jacob, what word
should we use to describe a building?
Jacob: Volume.
Teacher: So lets talk about the most volume. Then we'll talk
about how tall it is. All right. We are not going to use
biggest anymore. We are going to use words that
clearly describe what we are talking about.
- Which building is the tallest? (Building B, 2 units
tall)
- Which building is the widest? (Building A,
3 units wide)
- Which building takes up the most space? (Building A)
Discuss Volume. Show students the two models of
Sara's buildings you constructed with 8 cubes
and 9 cubes prior to the lesson. See Materials
Preparation.
- What do you notice about each of these shapes? (Possible responses: The shapes are made out of
connecting cubes; each shape looks different; one
is taller and one is shorter; the sizes are different.)
- How can you measure the amount of space occupied
by each shape? (Possible response: You can
count the cubes in each shape.)
- What do you call the amount of space each object
takes up? (volume)
- Which building takes up the most space? Which
building has the most volume? How do you know? (Building A, because it uses 9 cubes. Building B
uses only 8 cubes.)
Measure Volume. Refer students back to the
Marshmallows and Containers Lab in Unit 5.
- How did you compare the volume of the containers?
How did you find out how much each container
could hold? (I counted the number of
marshmallows that I could put in them.)
- How did you compare the volume of the buildings? (I counted the cubes in each building.)
- What if the cubes were different sizes? What
would happen if you constructed a building with
different-sized cubes? (I would have to be careful
comparing the volume of one building to another.
Two buildings that have the same number of
cubes might be different sizes because the cubes
were different sizes.)

Volume. Volume can be defined as the amount of space an
object takes up or as the number of cubic units it takes to fill
it. Students need to become familiar with the mathematical
terms and also be able to connect them with their own
language. Over the course of this unit, identify and define the
correct mathematical terms (face, cube, cubic unit, volume)
for the students. During discussions, refer to the
mathematical terms but also use them interchangeably with
language volunteered by the students, e.g., side, corner, etc.
You may find that it is difficult for students to cooperate
when building a model. Suggest that they each build a model
and compare them to see if they have the same result.
Students can also trade roles where one student builds and
the other checks each model.
Explain that when they construct buildings with connecting
cubes, one cube occupies one cubic unit of
space. So when they report the volume of Building A
and say it is "9 cubic units," other people will know
how much space the building takes up.
Refer students to the Find Volume pages in the
Student Activity Book. Remind students that they can
find the volume by answering the question, "How
many cubes does the model have?" They should
report the volume using cubic units. Students' strategies
for determining the volume may vary.
Before students begin the assignment, direct their
attention to Questions 2–3. After replicating Emily's
building, students will need to use those same cubes to
create a second building that is a different shape. They
will record their model on a building plan.
Display the Rules for Building Plans Master as you
explain these building restrictions:
- Cubes must always be properly connected.
- No balconies or arches allowed.
Show students examples of the buildings you prepared
prior to the lesson that don't follow these rules. See
Materials Preparation.
- Why are these rules needed for building plans to
make sense? How would you show a balcony or an
arch on a building plan? (You can't tell from looking
down if there are arches. It's hard to tell how
many columns there are when cubes are not
attached to one another.)
Have students complete the pages individually. Note
that Question 2B asks students to compare their model
of Emily's building with the one you made prior to the
lesson. See Materials Preparation and the building in
Figure 6.
Use Check-In: Questions 2–3 and the Feedback Box from the
Find Volume pages in the Student Activity Book to assess
students' abilities to apply the properties of addition (e.g.,
commutative, associative) to write number sentences that
represent the volume of a building [E3]; make connections
between a building of cubes, the building plan, and number
sentences [E4]; recognize that different shapes can have the
same volume [E6]; count and add cubic units to find volume
[E8]; show work [MPE5]; and use labels to show what
numbers mean [MPE6].
Share Strategies for Finding Volume. Upon completion,
direct students' attention to Question 2D on the
Find Volume pages. Discuss students' strategies for
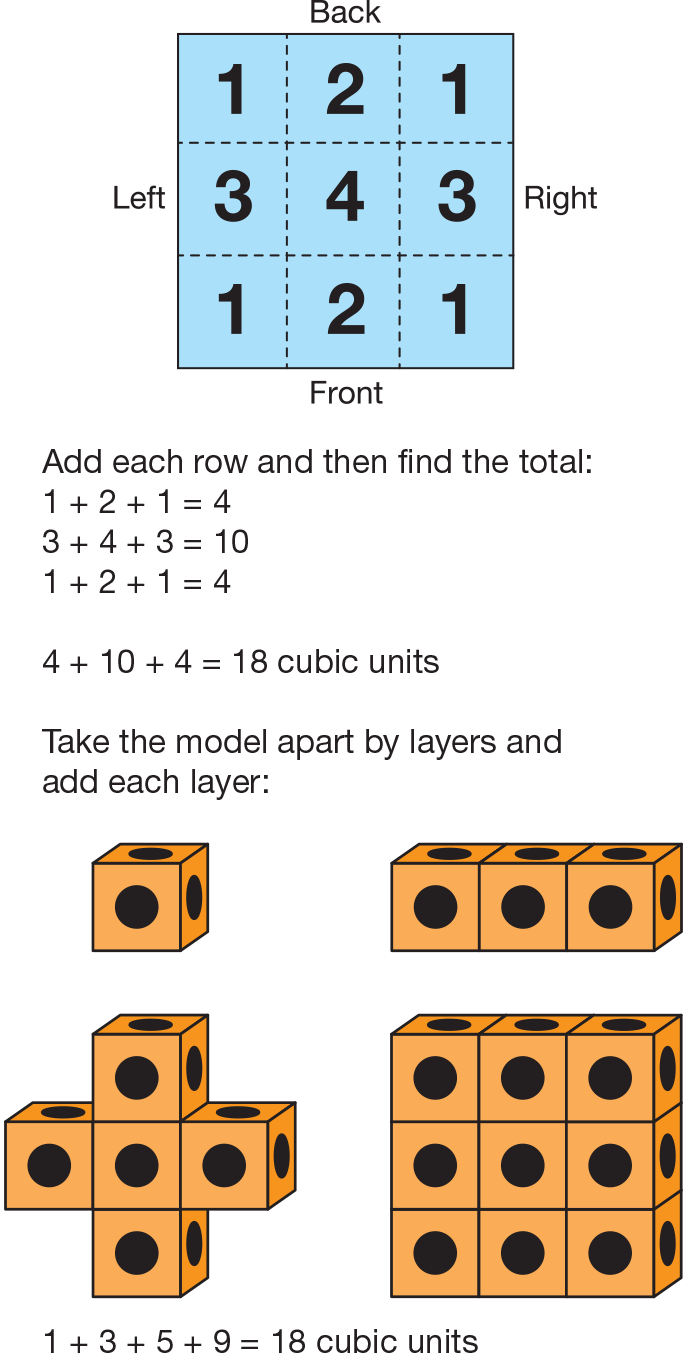
finding the volume of Emily's building.
- How did you find the volume of Emily's building?
Encourage students to brainstorm as many approaches
as they can. For example, some students may have
counted the individual cubes while others may have
counted by rows, columns, or layers and then added.
See Figure 6. Invite students to share their number
sentences describing the volume. Have students point
out what each number in their number sentences corresponds
to on the plans.
As students share their strategies and number sentences,
discuss two properties of addition. The commutative
property of addition states that numbers
(from the building plan for example) can be added in
any order. The associative property of addition states
that numbers can be grouped and added any way and
the sum will not be affected. Students will apply these
properties when they choose how to add the numbers
together to find the volume.