Properties of Addition

Students use the context of finding the volume of buildings to explore and apply the properties of addition. The cubes can be grouped and organized in different ways to encourage students to represent the quantity of cubes in a variety of ways. Students then apply these properties to solve riddles and find missing information about the buildings.

Students have been applying these properties, but this context allows students to develop strategies for adding more than two or three addends in more than one way. It is important that students apply these addition properties to larger numbers and in other contexts. This understanding and flexibility is the basis of students' mental math strategies and computational fluency.

Volume

Children develop ideas about space through action (Piaget and Inhelder, 1967). The more experiences students have exploring space, the better is their spatial visualization and imagery.

This unit develops students' visualization skills while exploring the concept of volume through the construction of models (buildings) with cubes. See Figure 1.

Students measure the volume of the buildings in cubic units. One of the ways is by counting the connecting cubes that make up the building. The volume is the amount of space that is occupied by the building. Students can relate this idea to their experiences counting the number of marshmallows that filled containers to compare the volumes (the space inside) of the containers.

Emphasis in this unit is placed on the difference between length and volume. Students measured length in centimeters when they measured the distance cars rolled in Unit 4. Here, students measure the length of the three dimensions of the buildings—front to back, left to right, and height. When measuring these distances, students can think of it as measuring on a number line. The answer is in units where the unit is the length of an edge of a cube.

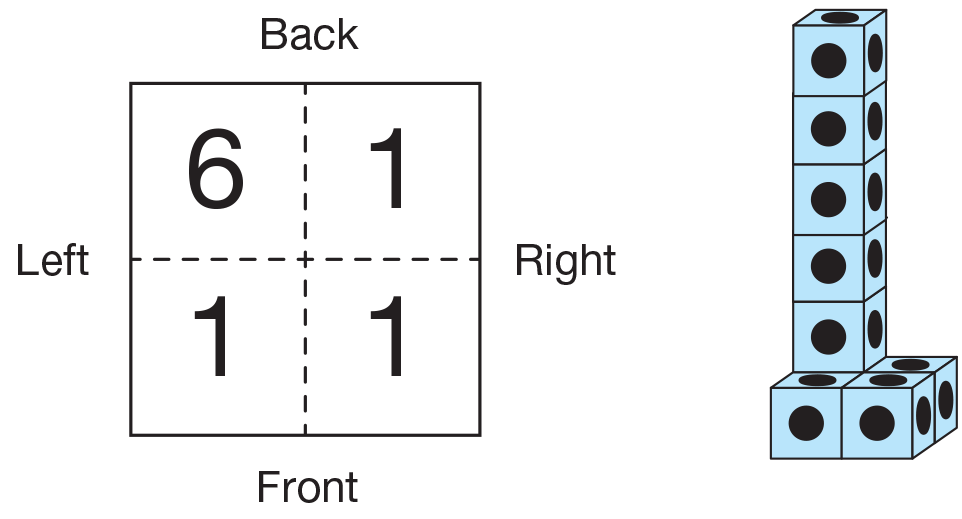
Figure 1: Building plan and building model

We are often asked to represent 3-dimensional objects in different ways. Architects, for example, create blueprints of individual floor plans, and builders make perspective drawings depicting how a structure will appear when viewed from different sides. Each method of representation has advantages and disadvantages. For example, Figure 2 shows two drawings of a structure built with cubes. The first drawing shows the front view of the structure. This view does not reveal what the other side of the structure looks like. The second drawing shows the rear view of the structure.

Figure 2: Front and rear views of a structure

When students build with connecting cubes and represent their structures on paper, they confront the same problems and challenges an architect encounters. In this unit, students construct buildings with connecting cubes and explore ways of recording and communicating the structure of their buildings to others. Buildings can be recorded on paper in a building plan that functions as a simple blueprint.

A building plan consists of numbers written on a square grid. The number in each square tells the number of cubes stacked over that square as shown in Figure 1. Building plans can describe only buildings that can be built by stacking cubes on a flat surface. They cannot describe a building with "balconies" or with "arches."

Subtraction Facts

Daily Practice and Problems items in this unit can be used to assess students' fluency with the subtraction facts related to the addition facts in Group B (3 − 0, 4 − 0, 5 − 1, 5 − 4, 6 − 1, 6 − 5, 7 − 1, 7 − 2, 7 − 5, 7 − 6, 8 − 1, 8 − 2, 8 − 3, 8 − 5, 8 − 6, 8 − 7, 9 − 1, 9 − 8). Counting-on, counting-up, and counting-back strategies are most commonly used to solve these facts.

Resources

• Battista, M.T. "The Importance of Spatial Structuring in Geometric Reasoning." In Teaching Children Mathematics. pp. 170–177. National Council of Teachers of Mathematics, Reston, VA., November, 1999.
• Clements, D.H. "Geometric and Spatial Thinking in Young Children." Opinion Paper for the National Science Foundation, Arlington, VA, 1998.
• National Research Council. "Developing Mathematical Proficiency Beyond Number." In Adding It Up: Helping Children Learn Mathematics, pp. 181–229. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
• Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
• Piaget, J., and B. Inhelder. The Child's Conception of Space. W.W. Norton, New York, 1967.