Connect Base-Ten Pieces, Hoppers, and Number
Sentences. Review with students what a base-ten
hopper can and cannot do on a number line:
- The base-ten hopper can only jump by ones, tens,
and hundreds.
- The base-ten hopper can move forward and
backwards.
- The base-ten hopper can start and stop at any
number on the number line.
- The number above each hop tells how far the
base-ten hopper moved.
- If the hop has a plus (+) sign, the base-ten hopper
moved forward.
- If the hop has a minus (−) sign, the base-ten
hopper moved backward.
Use the display of the Open Number Lines Master
and base-ten pieces to ask students how they would
represent the number 1111 on the number line.
Display the pack, flat, skinny, and bit and ask:
- What number am I showing? (1111)
- How would you write 1111 using digits? (1111)
- How is a hop of 1000 different from a hop of 100? (Possible response: It's a larger jump.)
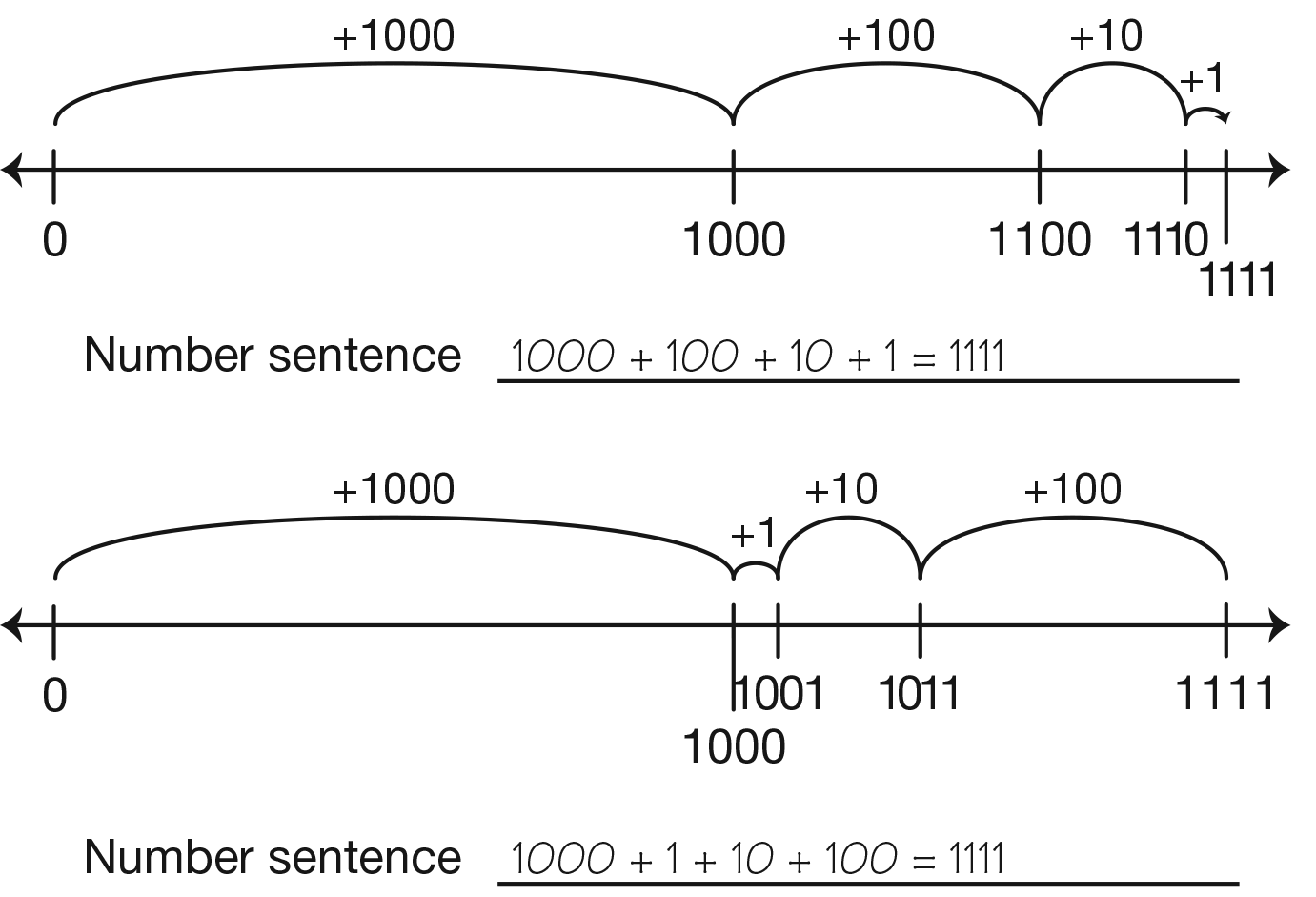
- Show how the base-ten hopper can hop on the
number line to reach this number. (See Figure 3.)
- What is a number sentence that represents the
hops on the number line? (Possible response:
1000 + 100 + 10 + 1 = 1111)
- How can you show 1111 with base-ten shorthand? (See Figure 4.)
Some second-grade students have difficulty with the concept
of writing numbers into the hundreds and thousands. They
may write 1000269 for 1269 and 30064 for 364. Help
students understand the value of each of the base-ten pieces
and how to write the expanded form of numbers. Place value
activities and games such as Take Your Places Please in Unit
6 will help students gain experience in writing numbers
correctly.
Students may draw the hops starting with different
base-ten pieces. For example, a student may draw
hops starting with the pack and then move to the flat,
skinny, and bit (1000 to 1100, to 1110, to 1111), and
another could start with the bit and move to the
skinny, flat, and pack. See Figure 3 for representations
of ways to show 1111 on the number line using
base-ten hoppers.
Next, ask students how they would represent the
number 1324 with base-ten pieces using the Fewest
Pieces Rule and on the number line.
- How did you represent 1324 with base-ten pieces? (1 pack, 3 flats, 2 skinnies, 4 bits)
- Is this using the Fewest Pieces Rule? How do you
know? (Yes; I know because I can't make any
trades.)
- How can you show 1324 with base-ten shorthand? (See Figure 5.)
- How can you show the number 1324 on the number
line? (1 hop of 1000, 3 hops of 100, 2 hops of
10, 4 hops of 1)
- What is a number sentence for the base-ten hops? (1000 + 100 + 100 + 100 + 10 + 10 + 1 + 1 + 1
+ 1)
- How can you write a number sentence using
expanded form to represent the hops on the number
line? (Possible response: I can combine the
hops that are the same size: 1 hop of 1000 =
1000, 3 hops of 100 = 300, 2 hops of 10 = 20,
and 4 hops of 4 = 4. The number sentence is
1000 + 300 + 20 + 4 = 1324.)
Show students a few more collections of base-ten
pieces (up to 1200) and ask students to show the
number on the number line with hops of the base-ten
hopper, to write the number using base-ten
shorthand, and to write a number sentence using the
expanded form.
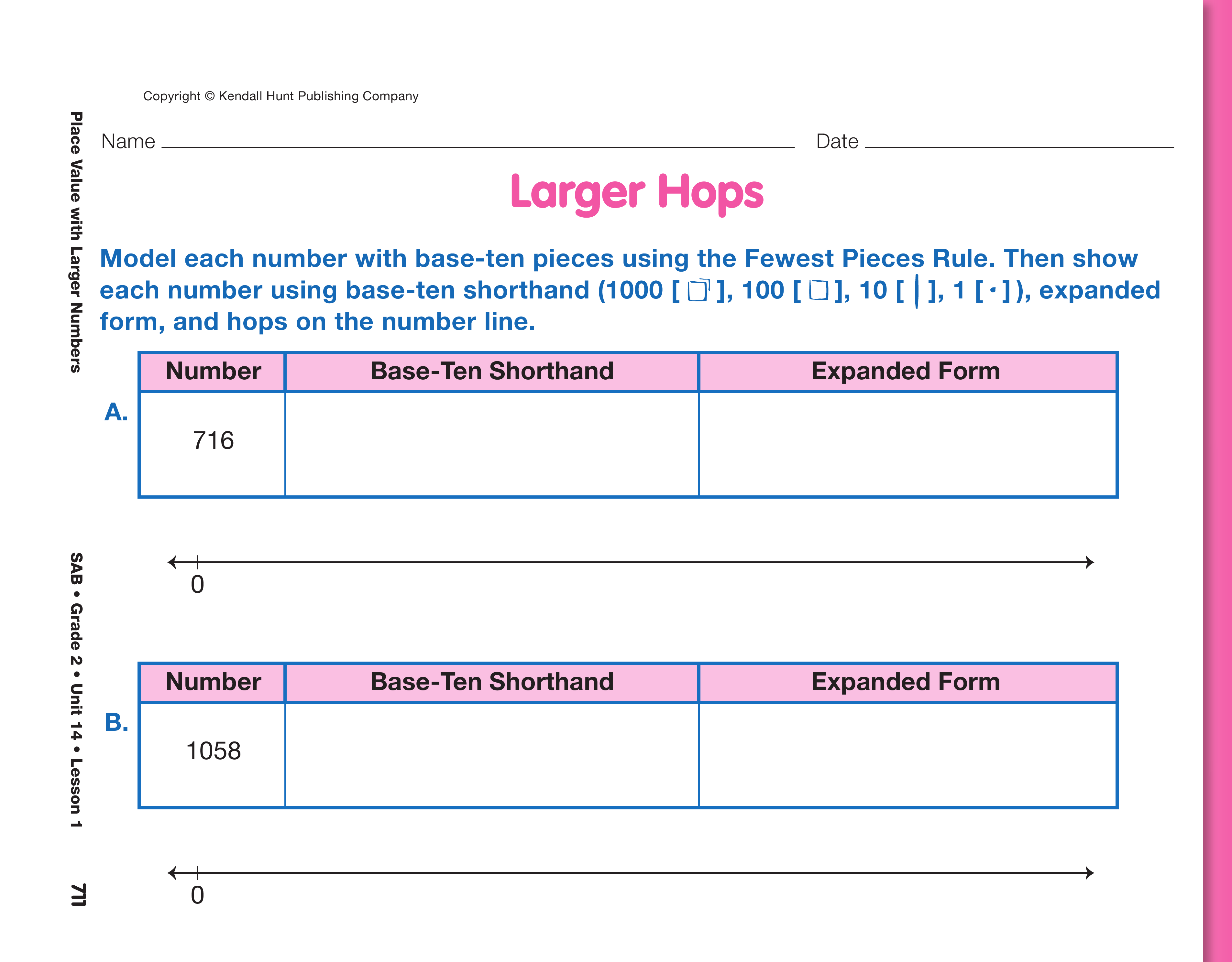
Have student pairs work on the Larger Hops pages
in the Student Activity Book. Students worked on a
similar activity in Unit 6 with numbers into the hundreds.
This activity includes numbers into the thousands.
Ask students to model each number with
base-ten pieces using the Fewest Pieces Rule, represent
each number on the number line with base-ten
hops, and write a number sentence using the
expanded form. Remind students to make their hops
of 1000 larger than their hops of 100.
As students work in pairs, ask questions such as the
following:
- Does your model of the number use the Fewest
Pieces Rule?
- How can you show the difference between a hop
of 1000 and a hop of 100? (Make it larger.)
- How does the number sentence using the
expanded form match the base-ten hops on the
number line? (Possible response for 568: I made
5 hops of 100 which is equal to 500, 6 hops of
ten which is equal to 60, and 8 hops of one which
is equal to 8. My number sentence is
500 + 60 + 8 = 568.)
- How are base-ten pieces, the hops on the number
line, and the expanded form alike or different? (Possible response: They all show the same number.
The 1000 is like the pack, the 100 is like the
flat, the 10 is like the skinny, and the 1 is like the
bit. For the expanded form, you combine all the
hops of 1000, the hops of 100, the hops of 10,
and the hops of 1 to write the number sentence.)
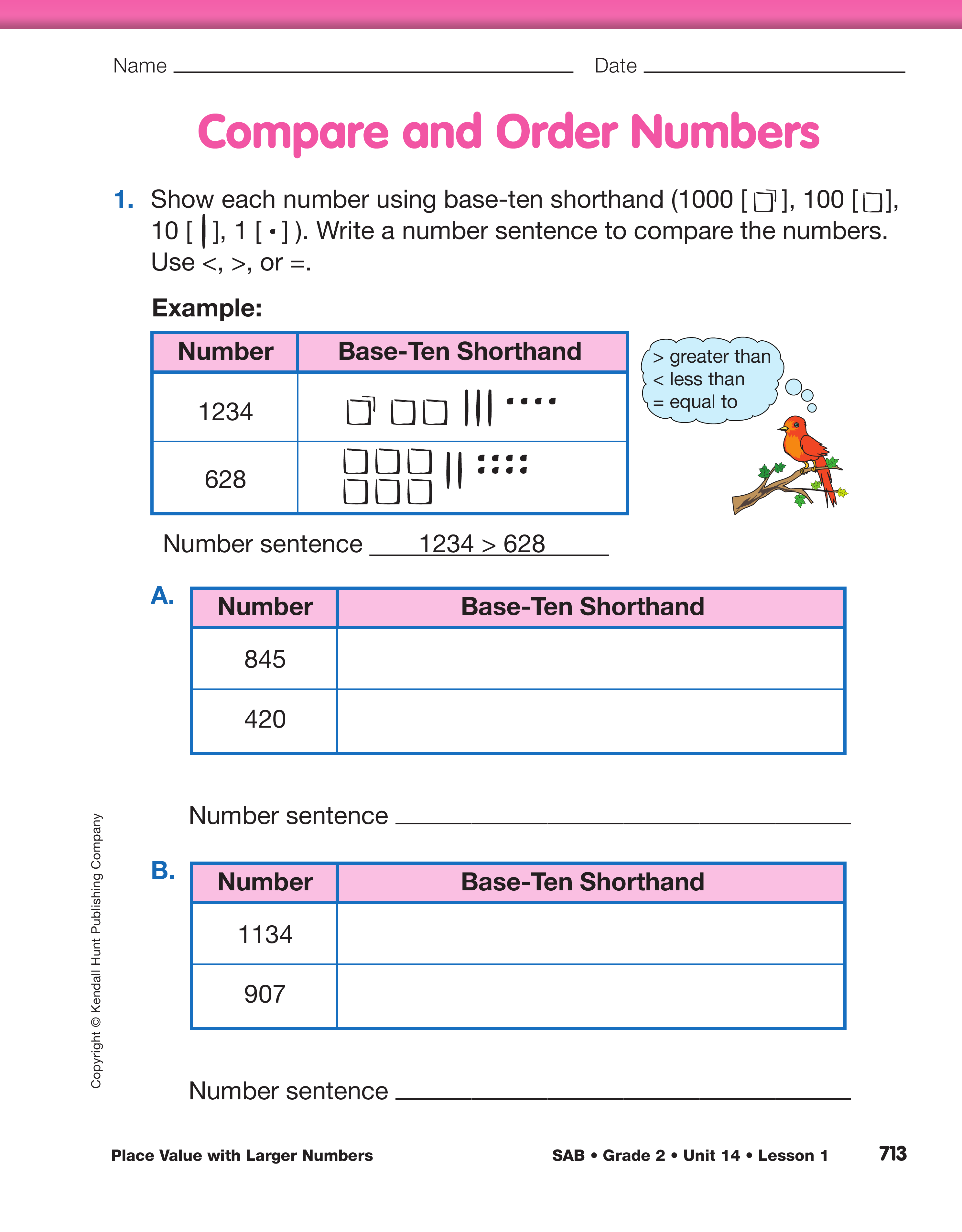
Compare and Order Multidigit Numbers. Ask
students to work with a partner to display 1 pack,
2 flats, 8 skinnies, and 2 bits in one group and
1 pack, 2 skinnies, and 3 bits in another group. See
Figure 6.
- What number is represented by each group of
base-ten pieces? (1282 and 1023)
- Which number is larger? (1282)
- How can you tell? (Possible response: They both
have a pack, but 1282 has 2 flats and 1023 has
0 flats.)
- If you didn't have base-ten pieces, how could you
tell which number is larger? (Possible response:
Since they both have thousands, I would look at
the thousands column first to see which number
has more thousands. If these digits are the same,
I would go to the hundreds column and see
which number has more hundreds, and so on.)
- How would you represent these numbers using
expanded form? (1000 + 0 + 20 + 3 = 1023 or
1000 + 20 + 3 = 1023 and 1000 + 200 + 80 + 2 =
1282)
- What number sentence could you write to compare
these two numbers? (1023 < 1282;
1282 > 1023)

In Unit 6, a Content Note addressed discussion points about
comparing three-digit numbers. The same points can be
applied to four-digit numbers:
- Each representation uses the Fewest Pieces Rule.
- The total number of base-ten pieces does not determine
which number is greater.
- Use the names of the pieces and the place value of the
digits interchangeably. For example, for the numbers
1214 and 1402, a student may say, "I see that there is
1 pack in both numbers. One number has 2 flats and the
other number has 4, so I know the one with 4 flats is
larger." You can respond, "So you know that the
thousands are the same and that 4 hundreds is more
than 2 hundreds."
- When comparing numbers, encourage students to think
of the size of the pieces that represent the numbers so
that they create visual images of the numbers.
- If in two 4-digit numbers, one number has more packs
than the other number, the one with more packs is the
greater number.
- If in two 4-digit numbers, the number of packs is the
same, the one that has more flats will be the greater
number.
- If in two 4-digit numbers, the number of packs and flats
is the same, the one with more skinnies will be the
greater number.
- If in two 4-digit numbers, the number of packs, flats,
and skinnies is the same, the one with more bits will be
the greater number.
Next have student pairs display 8 flats, 7 skinnies,
and 2 bits in one group and one pack, 2 flats,
1 skinny, and 6 bits in another group. See Figure 7.
- What number is represented by each group of
base-ten pieces? (872 and 1216)
- Which number is larger? (1216)
- How can you tell? (Possible response: The number 1216 has digits into the thousands place and
the number 872 only has digits to the hundreds
place.)
- How would you represent these numbers using
the expanded form? (800 + 70 + 2 = 872 and
1000 + 200 + 10 + 6 = 1216)
- What number sentence could you write to compare
these two numbers? (872 < 1216;
1216 > 872)
For each of the following pairs of multidigit numbers,
ask students to represent the numbers with
base-ten pieces using the Fewest Pieces Rule. Then
ask them to decide which number is larger and to
write a number sentence using < or > to compare the
numbers. See the Sample Dialog.
- 345 and 369
- 476 and 468
- 1214 and 1402
- 1323 and 1268

Use this Sample Dialog to guide your discussion of
comparing numbers to a thousand.
Teacher: When you compare two numbers like 1323 and
1268, how can you tell which is larger?
Mark: I use base-ten pieces to represent the numbers. For
1323, I used one pack, 3 flats, 2 skinnies, and 3 bits.
For 1268, I used one pack, 2 flats, 6 skinnies, and
8 bits. I counted all the pieces for each number. For
1323, I used 9 pieces and for 1268, I used 17 pieces, so
1268 is larger.
Teacher: What do you think of Mark's strategy?
Michael: I don't think that's right. You're not supposed to
count the number of pieces. You have to think of the
size of each of the base-ten pieces. A pack is the same
as a thousand bits. The number 1000 is larger than 29
even though 29 has more pieces.
Chloe: That's right. It's like when you're counting money. You
have to think of the value of each coin. A dime is not the
same as a penny and a ten is not the same as a one.
Teacher: Does anyone else have any ideas?
Karly: I write the numbers in expanded form: 1323 is 1000 +
300 + 20 + 3 and 1268 is 1000 + 200 + 60 + 8. That
helps me to think of the value of each digit. If I think of
the one in the thousands place as 1000, the 3 in the
hundreds place as 300, the 2 in the tens place as 20,
and the 3 in the ones place as 3, I can add them and I
get 1323.
Teacher: What else do you have to think about when you
compare numbers?
Lauren: When I use base-ten pieces to compare numbers I
make sure I use the Fewest Pieces Rule. That helps me
to compare thousands to thousands, hundreds to
hundreds, and so on.
Teacher: That's a good point. After you make all the trades
you can make, what do you do next?
Connor: I start with the packs. If they have a different
number of packs, the number with more packs is larger.
If both numbers have the same number of packs, I go to
the flats. If they both have the same number of flats, I
keep going to the skinnies and bits. If they have a
different number of flats, I see which one has more and
that's the larger number.
Teacher: That's a great strategy. What can you do if you
don't have base-ten pieces?
Brandon: I just looked at 1323 and 1268. Since both
numbers have thousands, I looked at the rest of the
numbers. I know that 323 is larger than 268, so 1323 is
larger than 1268.
Teacher: Great thinking, class! You showed me that you
have a good understanding of place value.
Ask students to display 1 pack, 3 flats, 8 skinnies,
and 4 bits in one group and 1 pack, 2 flats, 18 skinnies,
and 4 bits in another group. See Figure 8.
Have
students work with a partner to answer the following
questions:
- Which set of base-ten pieces represents the larger
number? How do you know? (Possible response:
They are both the same number. When I used the
Fewest Pieces Rule, I traded 10 of the 18 skinnies
for a flat and I got the same answer.)
- What number do both sets represent? (1384)
- What number sentence can you write to represent
each number? (1000 + 300 + 80 + 4 and
1000 + 200 + 180 + 4)
Using the Fewest Pieces Rule, have a student
demonstrate how to trade 10 of the 18 skinnies for a
flat so that students can see that the two sets of
pieces represent the same number.
- Is this a true statement: 1000 + 300 + 80 + 4 =
1000 + 200 + 180 + 4? Explain how you know. (Possible response: Yes; after we made all the
trades we could make, we had the same number.
If you add the numbers, you'll get the same
answer.)
Ask students to display 1216, 527, and 1024 with
base-ten pieces using the Fewest Pieces Rule. Then
have students display them in order from smallest to
greatest.
- How do you know which number is the greatest?
How do you know which number is the smallest?
How do the base-ten pieces help you determine
the order of the numbers? (Possible response:
The pack is the largest piece, so if a number has
packs it's larger than a number that doesn't have
any packs. I know 1216 and 1024 are larger than
527. Since 1216 and 1024 both have packs, I
look at the flats next and 1216 has two flats and
1024 has no flats. The order is 527, 1024, and
1216.)
- When you compare numbers and place them in
order, do you count the number of pieces to find
out which number is greater or smaller? (No, the
packs, flats, skinnies, and bits all have a different
value. A pack is not the same as a flat—the pack
has 1000 bits and the flat has 100.)
Have a student demonstrate how to place the three
numbers on the display of the Open Number Lines
Master.
- What number is the smallest? (527)
- Should we place that number on the left or the
right on the number line? (left)
- What number comes next? (1024)
- What is the last number? (1216)
- Should 1024 be closer to 1216 or 527? How do you
know? (Possible response: It should be closer to
1216 because 527 is about 500 away from 1000
and 1216 is about 200 away from 1000.)
Assign the Compare and Order Numbers pages in
the Student Activity Book. Upon completion, use a
display of the page to ask students to explain how
they determined the order of some of the numbers.
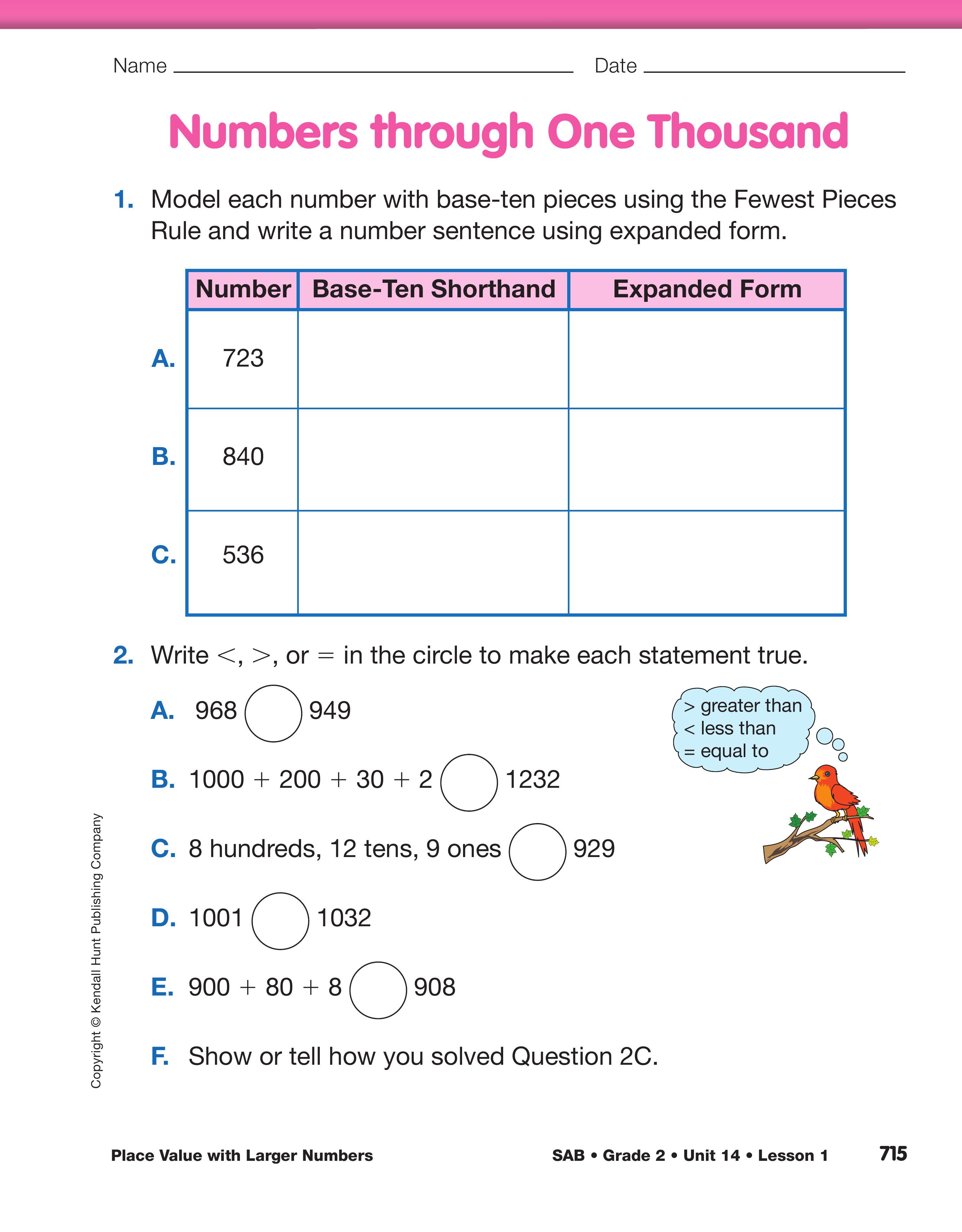
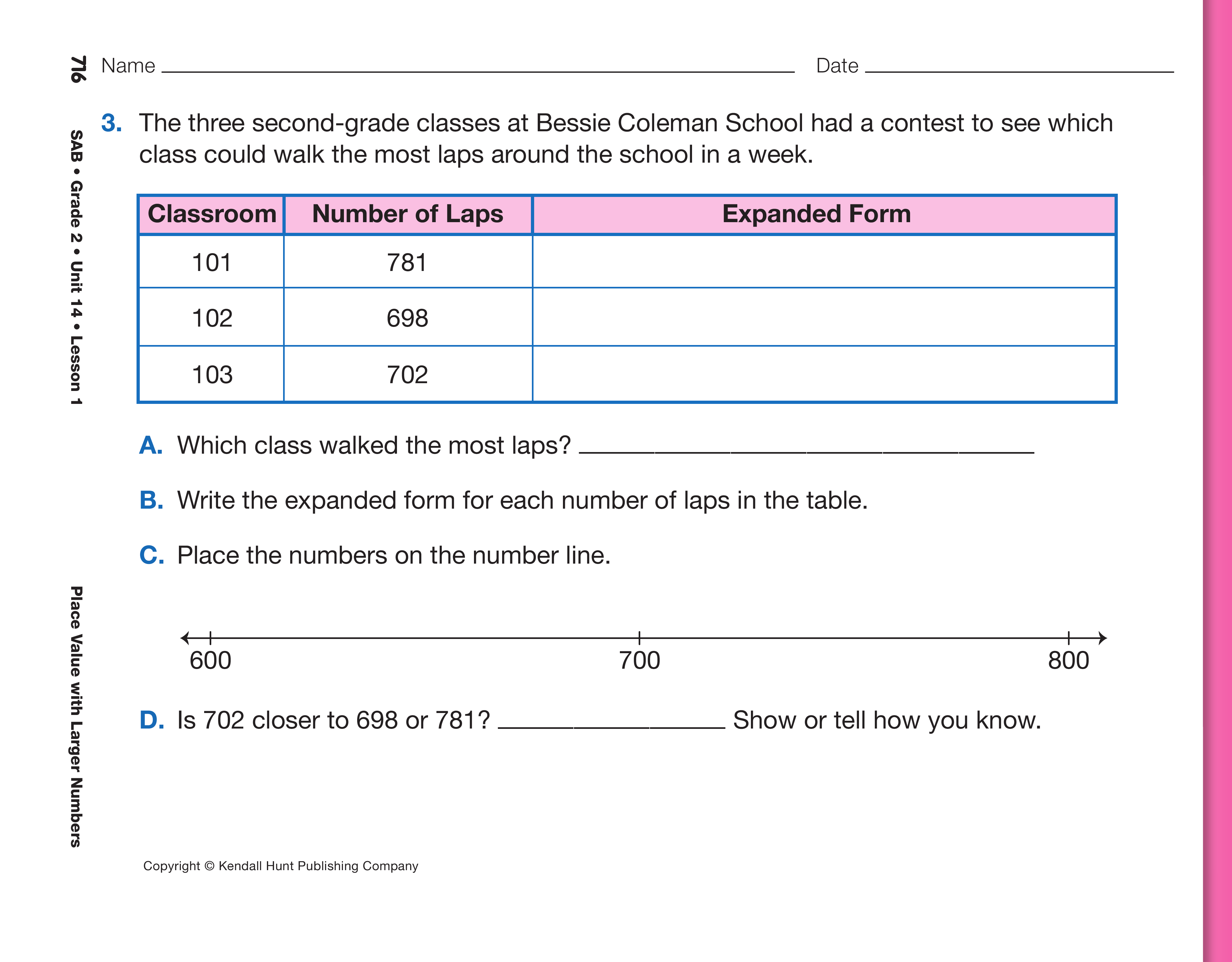
Assign the Numbers through One Thousand pages
in the Student Activity Book to assess students'
understanding of place value to a thousand. Have
base-ten pieces readily available.
Assign the Numbers through One Thousand pages with the
Feedback Box in the Student Activity Book to assess
students' abilities to use and apply place value concepts to
make connections among representations of multidigit
numbers [E1]; compose and decompose numbers using
ones, tens, hundreds, and thousands [E2]; show and
recognize different partitions of multidigit numbers using
different representations [E3]; and compare and order
multidigit numbers [E4].