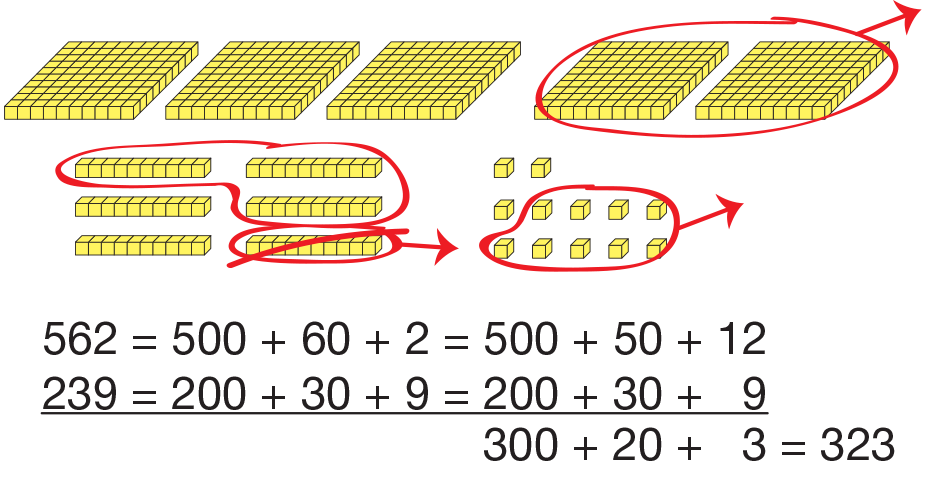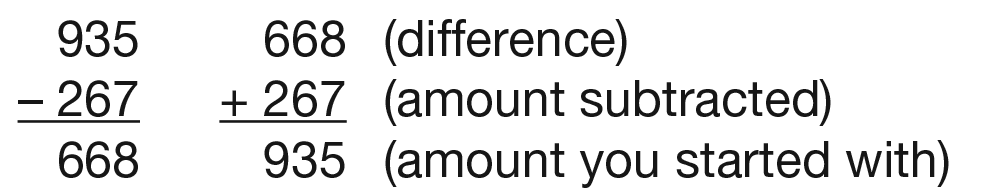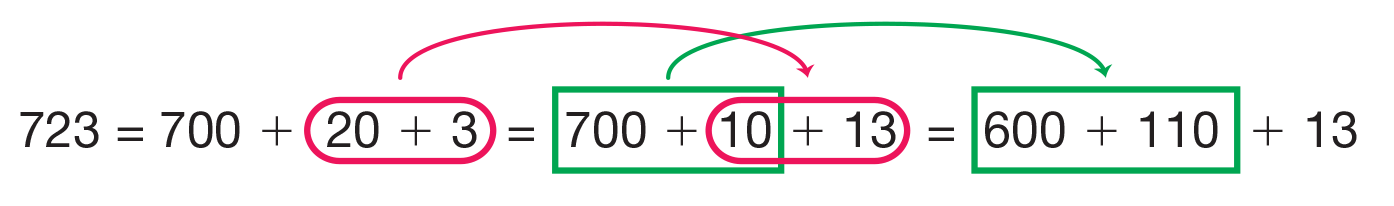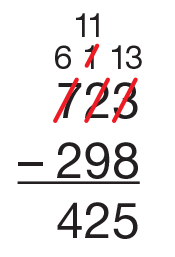Subtracting Multidigit Numbers

Est. Class Sessions: 3

Developing the Lesson

Part 1: Making Connections between Strategies

Use Base-Ten Pieces. Distribute base-ten pieces to students to solve the problem 562 − 239. When modeling subtraction, ask students to place the first number in the problem, the minuend, 562. They will show the subtraction by taking away pieces that represent the second number, the subtrahend, 239. As students work with the base-ten pieces, be sure they do not begin the problem by laying out the pieces for both numbers.

Ask questions similar to the following that make connections between the base-ten pieces and the symbols in the numbers:

How did you model 562? (5 flats, 6 skinnies, and 2 bits)
If you had a group of 562 things, could you take 239 things away? (yes)
If you had a group of 239 things, could you take 562 things away? (no)
Which number is greater, 562 or 239? (562)
How do you know? (Possible response: 562 has 5 flats or 5 hundreds and 239 has only 2 flats or 2 hundreds so 562 is greater than 239.)
Which of your pieces represents 60? How do you know? (the 6 skinnies; each skinny is a ten so 10, 20, 30, 40, 50, 60)
Which digit has a value of 500? How do you know? (the 5, because it is in the hundreds place)
How did you represent 500? (5 flats) And 2? (2 bits)
Think about the numbers 562 and 239 and the base-ten pieces that represent the numbers. Is there a big difference between the two numbers? A little difference? Why do you think so?
What strategies can you use to estimate the difference? (Possible response: If I just look at the hundreds, 500 − 200 is 300.)
Is there another way to estimate the difference? Explain your strategy.

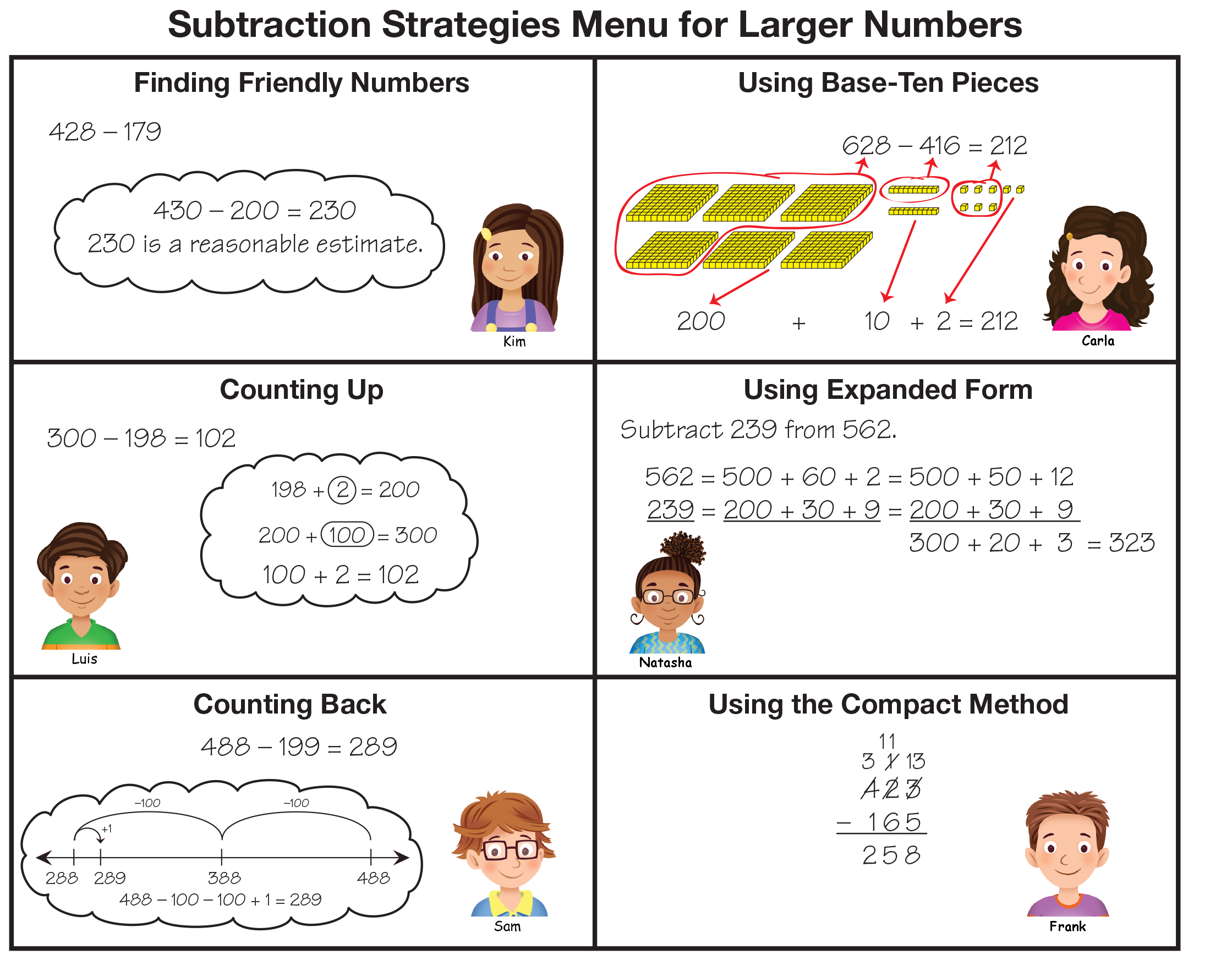
Remind students that in Lesson 4 they used some of the following strategies to estimate differences:

Using Friendly Numbers (changing only one number, usually the number to be subtracted)
Using Friendly Numbers (nearest hundred)
Using Friendly Numbers (nearest ten)
Subtracting Hundreds
Counting Back on the Number Line
Thinking Base-Ten Pieces

Regroup Using Expanded Form. Display and direct students' attention to the Subtraction Strategies Menu for Larger Numbers page in the Student Activity Book Reference section. See Figure 1. Continue to discuss the same problem, 562 − 239, asking students to relate the base-ten pieces to the problem written in expanded form on the menu. See Figure 2.

Remind students that this is a subtraction problem. The plus signs in the problem written this way simply refer to the different ways of partitioning the numbers. This doesn't change it from a subtraction problem. See the Content Note. Draw students' attention to the way the columns are aligned in this notation so that hundreds are subtracted from hundreds, tens are subtracted from tens, and ones are subtracted from ones.

We intentionally left the subtraction sign out of the expanded form solution to the problem. Including it only on the left would make a mathematically incorrect sentence. A correct sentence would be − 623 = −(600 + 20 + 3), but students haven't worked with parentheses yet, so this would be confusing. If students become confused by the presence of the plus signs in a subtraction problem, try writing the expanded form like this:

864 = 800 and 60 and 4
623 = 600 and 20 and 3
200 and 40 and 1 = 241

With each student still modeling 562 with base-ten pieces, ask:

How does the problem written this way relate to the base-ten pieces? How is the 500 + 60 + 2 shown in your base-ten pieces? (That is what I am starting with: 5 flats, 6 skinnies, and 2 bits.)
What does the 200 + 30 + 9 in the example on the menu stand for? (That is what I need to take away, 239.)
Can you start subtracting right away? Can you take 9 bits from 2 bits? (No, I need to make a trade.)
What will you trade? (1 skinny for 10 bits or 1 ten for 10 ones)
Trade 1 skinny for 10 bits. How many skinnies do you have now? (5 skinnies) How many bits? (12 bits)
How is trading one skinny (1 ten) for ten bits (10 ones) shown in the expanded form example on the menu? (Natasha rewrites 60 + 2 as 50 + 12.)
Does 500 + 60 + 2 equal 500 + 50 + 12? Do you still have 562 base-ten pieces? (yes) [See Content Note.]
Now can you subtract? Can you take 9 from 12? (yes)

Students frequently do not understand that when they make trades (or regroup) in order to subtract they are just partitioning the top number in a different way. It is important for them to realize that the new representation should have the same value.

For example: 500 + 60 + 2 = 500 + 50 + 12.

Finish working through the example problem. Compare the difference on the menu, 323, to the number of base-ten pieces students show in their answers.

Ask:

How does your answer compare with your estimates? Does this difference seem reasonable?

Display another problem such as 325 − 146, which requires two trades. Have the class first estimate the difference. Then ask students to place 325 pieces. They will use base-ten pieces to solve the problem, step-by-step, as a volunteer demonstrates the trading with display base-ten pieces. You will record the expanded form notation steps.

Ask:

How can I write 325 in expanded form? (300 + 20 + 5)
How can I write 146 in expanded form? (100 + 40 + 6)

Display the notation:

325 = 300 + 20 + 5
146 = 100 + 40 + 6

Ask:

How does 300 + 20 + 5 match with your base-ten pieces? (It is like the 3 flats, 2 skinnies, and 5 bits we are starting with.)
Can you begin subtracting right away? Can you take 6 bits from 5 bits or 4 skinnies from 2 skinnies? (no)
What can you do? (I can trade 1 skinny for 10 bits.)

Tell students to make the first trade with their base-ten pieces.

How many skinnies do you have now after the trade? (1 skinny) How many bits? (15 bits)

Extend the notation by writing:

325 = 300 + 20 + 5 = 300 + 10 + 15
146 = 100 + 40 + 6 = 100 + 40 + 6

Ask:

How did I show in expanded form that you traded 1 skinny for 10 bits? (You rewrote 300 + 20 + 5 to read 300 + 10 + 15.)
What do you notice about this problem? Are you ready to start subtracting? Can you subtract 6 from 15? (I can subtract 6 from 15, but I can't subtract 40 from 10.)
What should you do with your base-ten pieces? (Trade a flat for 10 skinnies.)

Tell students to demonstrate the trade with their base-ten pieces.

Ask:

How many flats do you have left after the trade? (2 flats)
How many hundreds is that? (2 hundreds)
How many skinnies do you have now? (11 skinnies)
How many tens is that? Count by tens. (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110)
Do you still have 15 bits? (yes)
How should I show these trades in expanded form? [See below.]

Continue writing the problem in expanded form as you make connections between the notation and the base-ten pieces. Write:

325 = 300 + 20 + 5 = 300 + 10 + 15 = 200 + 110 + 15
146 = 100 + 40 + 6 = 100 + 40 + 6 = 100 + 40 + 6

Show the subtraction steps as you remind students to subtract hundreds from hundreds, tens from tens, and ones from ones. 200 minus 100 is 100, 110 minus 40 is 70, and 15 minus 6 is 9. Complete the problem by adding 100 + 70 + 9:

325 = 300 + 20 + 5 = 300 + 10 + 15 = 200 + 110 + 15
146 = 100 + 40 + 6 = 100 + 40 + 6 = 100 + 40 + 6
100 + 70 + 9 = 179

Compare Subtraction Menus. Display the Subtraction Strategies Menu in the Student Activity Book Reference section as you direct students to the new version of the menu, the Subtraction Strategies Menu for Larger Numbers in the Student Activity Book Reference section.

Ask:

How are these two subtraction menus the same? (The paper-and-pencil strategies and mental math strategies are the same.)
How are they different? (Possible responses: On the new menu, the numbers in the examples are bigger. They are all 3-digit numbers minus 3-digit numbers. You can't use the 200 Chart to count up or count back because the numbers are too big. The examples show a lot of trades.)
Are you familiar with all of the strategies on the new Subtraction Strategies Menu for Larger Numbers?
How could this menu be helpful to you? (I can use it when I am solving subtraction problems with larger numbers.)

Use a Variety of Strategies. Explain that students are going to use the Subtraction Strategies Menu for Larger Numbers to solve the same problem in many different ways so that comparisons can be made. Tell students to first estimate the difference for 935 − 267. Then ask student pairs to choose a way to solve the problem. This problem involves two trades. Guide students toward picking a strategy they feel confident using.

Ask:

Who can solve 935 − 267 using base-ten pieces or shorthand? a number line? a different mental math strategy? expanded form? the compact method? another way?

Give student pairs a piece of chart paper on which to display their solution strategies. Make sure all of the strategies are represented. After they solve the problem, ask students to display their solution strategies. See Figure 3.

Ask questions that make connections between the strategies such as:

How did [student names] show 900? 30? 5?
How did [student names] show 200? 60? 7?
How did [student names] show 267 in expanded form? (200 + 60 + 7)
On the number line? (2 hops of 100, 6 hops of 10, and 7 hops of 1)
Did [student names] make any trades with base ten pieces? (They traded 1 skinny for 10 bits and then 1 flat for 10 skinnies.)
[Student names] used the compact method. How did they show trades? (When they needed to trade a skinny for 10 bits, they crossed the number of skinnies out and wrote one less to show that one was traded. They wrote the new number of bits to show they added 10 bits to the number of bits that were there in the beginning. They did the same sort of thing when they traded a flat for 10 skinnies.)
[Student names] solved the problem using expanded form. Did they need to make any trades in order to subtract 267 from 935 or could they start subtracting right away? (They needed to make some trades.)
How did [student names] show trades when they used expanded form? (They kept writing different partitions for 935.)
What were some of the different number sentences [student names] used to show 935? (Possible responses: 900 + 30 + 5, 900 + 20 + 15, and 800 + 120 + 15)
Do all of these number sentences represent 935? (yes)
Did everyone get the same answer? (yes, 668)
How do the answers compare to your estimate? Does the answer seem reasonable?
Does one way seem more efficient than another when you are subtracting larger numbers? Why? (Possible responses: I don't always have base-ten pieces, so that's not always an efficient strategy. There were a lot of numbers to keep straight so the paper-and-pencil methods seem more efficient. There was less writing with the compact method than with expanded form.)

Check Subtraction with Addition. Remind students that there are many ways to check answers. Comparing an answer to an estimate is one way to see if the answer is reasonable. Another way to check the answer to a problem is to solve the problem another way. Students demonstrated that by solving the problem in a variety of ways. Students can also use addition to check their subtraction calculations. Review how to add the difference (668) to what was subtracted, the subtrahend (267), to see if they get the starting amount, the minuend (935). See Figure 4. Ask students to use addition to check their subtraction calculations.

Then ask:

When you added your answer to the number you subtracted, did you get the number you started with, 935?
Does this make sense? Why or why not? (Possible response: Yes, it makes sense because subtraction and addition are like opposites. If you start with an amount and take some away, you should be able to add that amount back and have the same amount.)

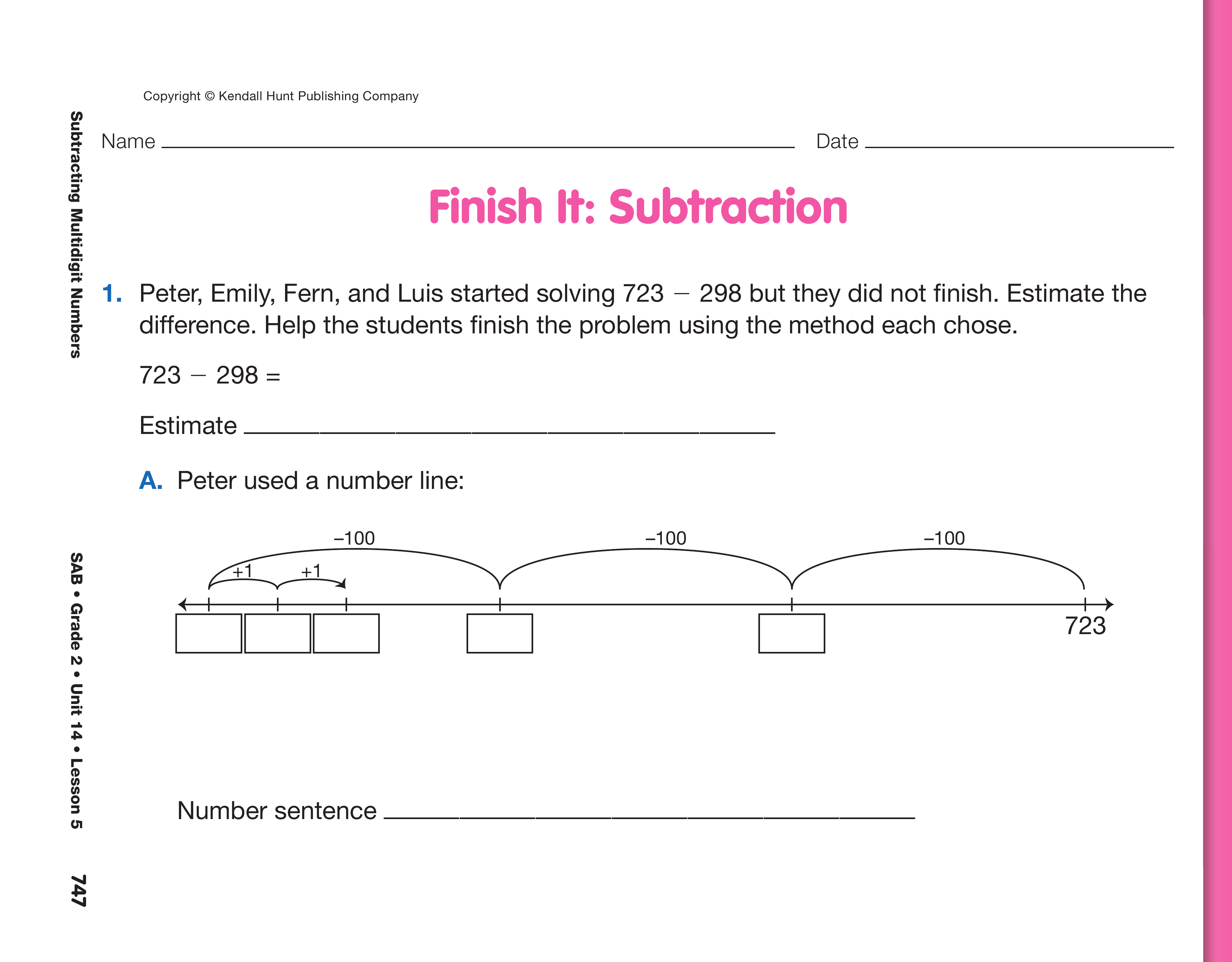
Finish It. Assign the Finish It: Subtraction pages in the Student Activity Book. Students will practice using a variety of methods to solve 3-digit subtraction problems and make connections among the strategies. They will use addition to check their subtraction.

Use Check-In: Questions 2–3 and the Feedback Box on the Finish It: Subtraction pages in the Student Activity Book to assess students' abilities to use and apply place value concepts to make connections among representations of multidigit numbers [E1]; subtract multidigit numbers using paper-and-pencil methods [E7]; check for reasonableness [MPE3]; and check calculations [MPE4].

Upon completion, use the following prompts to discuss students' work:

How did you estimate the difference for 723 − 298? (Possible response: I used friendly numbers. 700 − 300 is 400.)
Model the problem with base-ten pieces and solve it. What is your answer? (425)
How does this answer compare to your estimate? Is your answer reasonable?
Show how to check the problem using addition. (425 + 298 = 723)
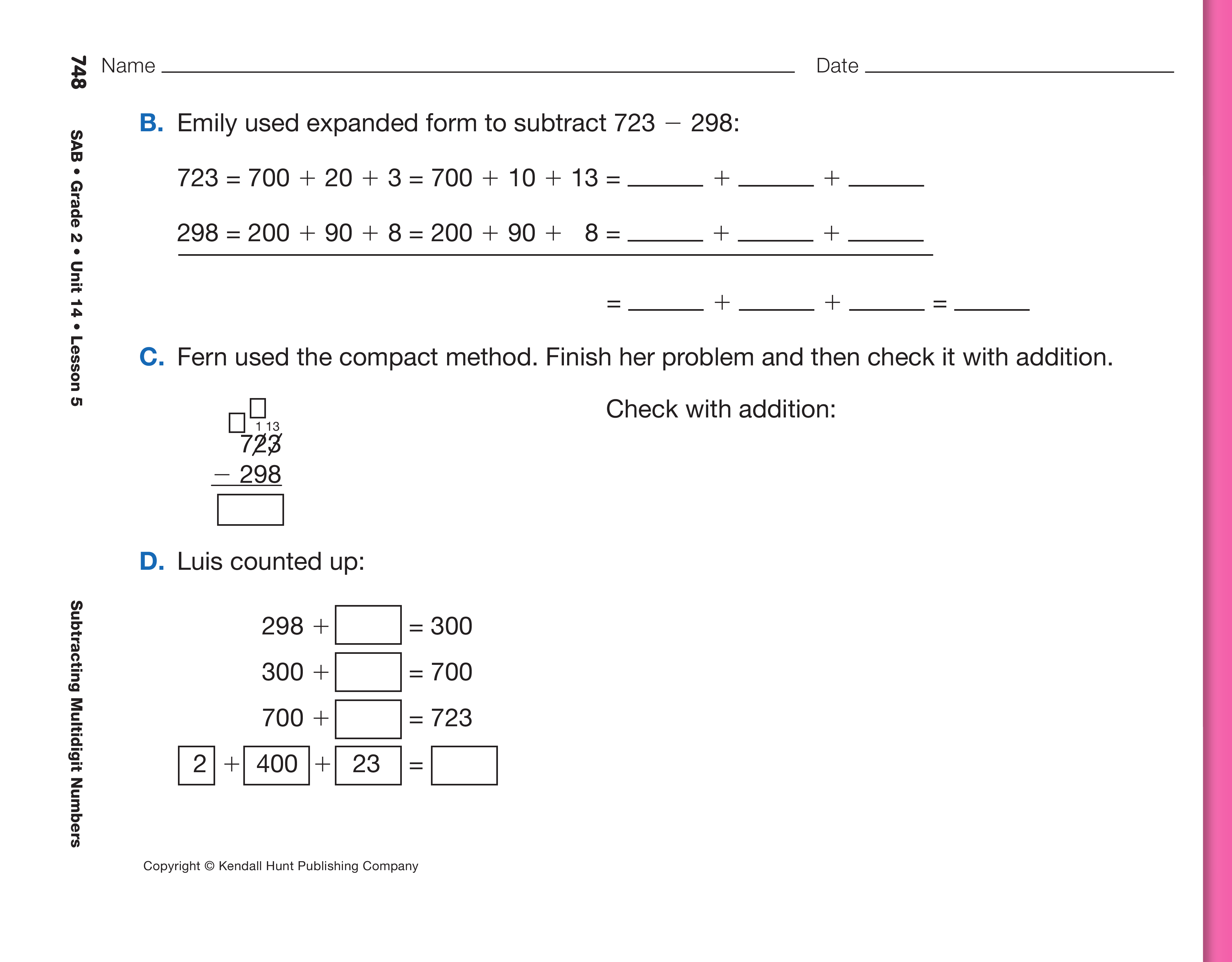
Look at Emily's work with expanded form in Question 1B. Explain the trades that were made. [See Figure 5.] (Two trades were made. She could not take 8 from 3. She needed to take 10 from the 20 to give the 3 ten more ones. 9 tens could not be taken from 1 ten, so 1 hundred was traded for 10 tens.)
Look at Fern's work with the compact method in Question 1C. Explain the trades that were made. [See Figure 6.] (The 2 is crossed out to show that 1 ten was taken from the 20 and 10 was left after the trade. A little 13 in the ones column shows that there were 13 ones after the trade. The 7 is crossed out to show that 1 hundred was taken from the 700 and the 6 shows that 600 was left after the trade. A little 11 in the tens column shows that there were 11 tens after the trade.)
Which strategy did you like the best? Why?