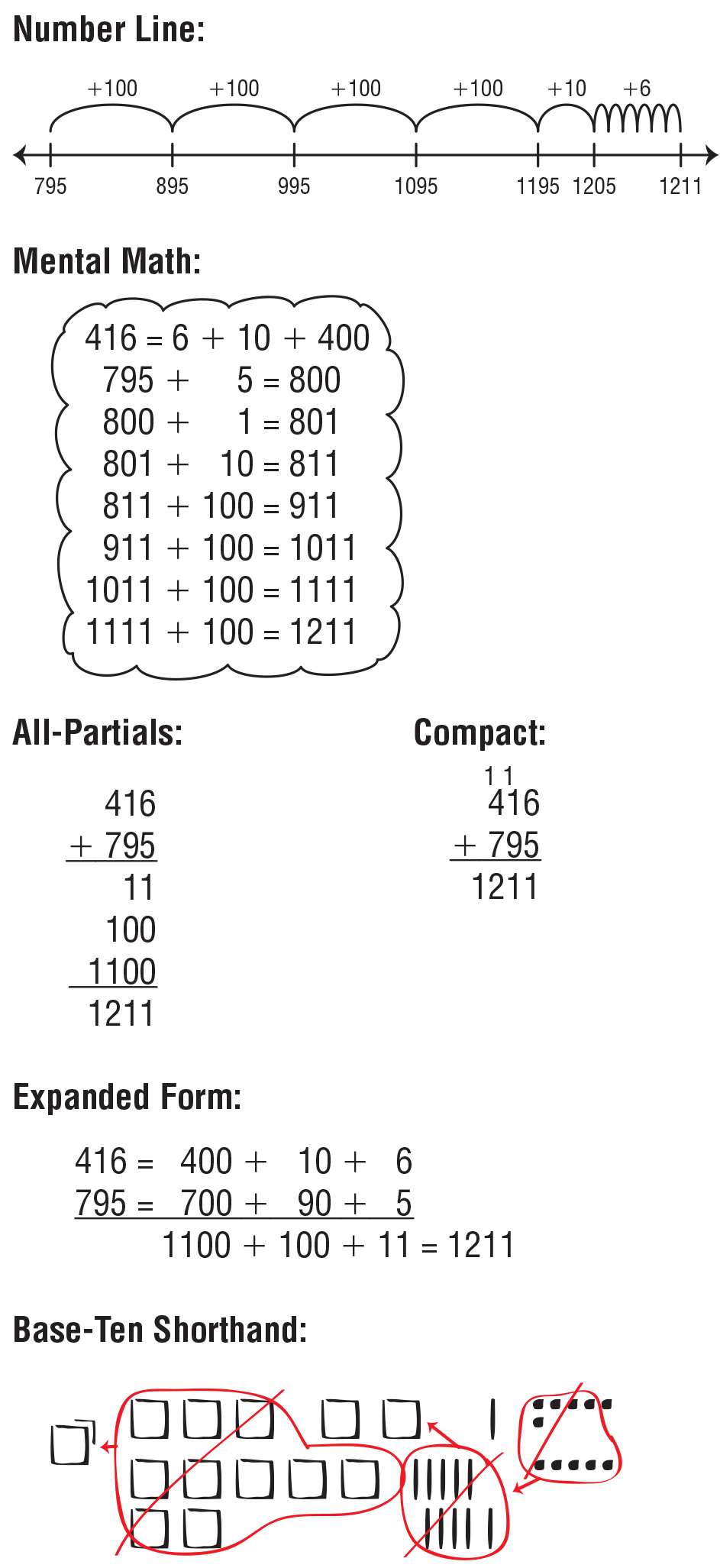Use Base-Ten Pieces. Distribute base-ten pieces to
students. Display the problem 768 + 325. Use a display
set of base-ten pieces to model the two numbers
in the addition problem using flats, skinnies, and bits
as students do the same.
Ask questions similar to the
following that make connections between the base-ten
pieces and the digits in the numbers:
- How did you model 768? (7 flats, 6 skinnies, and
8 bits)
- What is the value of the 7 in 768? (Possible
responses: 700, 7 flats, 70 tens)
- What is the value of the 6 in 768? (Possible
responses: 60, 60 bits, 60 ones)
- How did you model 325? (3 flats, 2 skinnies, and
5 bits)
- Which of your pieces represent 20? How do you
know? (the 2 skinnies; each skinny is a ten so 10,
20)
- How did you represent 300? (3 flats)
- Which strategies can you use to estimate the
sum? (Possible response: I look at the base-ten
pieces. Altogether, I have 10 flats and some
skinnies and bits so I know the sum is going to
be more than 1000.)
- Which base-ten piece represents 1000? Show me. (a pack)
- Is there another way to estimate the sum? Explain
your strategy.
Remind students that in Lesson 2 they used some of
the following strategies to estimate sums:
- Adding tens and hundreds
- Counting on by tens and hundreds
- Using friendly numbers
- Using dollars and coins
- Thinking about base-ten pieces
- Composing and decomposing numbers
- Use your base-ten pieces to find the sum of
768 + 325. Remember the Fewest Pieces Rule.
Can you make any trades? (Yes, I can trade
10 bits for 1 skinny. I can trade 10 flats for 1
pack.)
- What is the sum? (1093) [See Figure 1.]
- How does this compare with your estimates? Does
this sum seem reasonable?
- Why is there a zero in 1093? (0 hundreds; After I
trade 10 flats for 1 pack, or 10 hundreds for
1 thousand, there are no hundreds.)
- What does the 1 in 1093 represent? (one thousand)
- Is solving 768 + 325 a little different or a lot different
from solving problems like 48 + 55? What is
different? What is the same? (Possible response:
It is only a little different. The numbers I am
adding are bigger. The sum is in the thousands. I
have to make two trades. I can still use base-ten
pieces to solve it.)
- Could you still use the strategies on your Addition
Strategies Menu to solve this problem? (yes)
Use a Variety of Strategies. Explain that students
are going to solve the same problem in many different
ways so that comparisons can be made. Display
the Addition Strategies Menu from the Student
Activity Book Reference section. Tell students to first
estimate the sum of 416 + 795. Then ask student
pairs to choose a way to solve the problem. Guide
students toward picking a strategy they feel confident
using. See Content Note.
- Who can solve 416 + 795 using base-ten pieces or
shorthand? a number line? a different mental math
strategy? the all-partials method? expanded form?
the compact method? another way?
- Is using the 200 Chart to solve this problem helpful?
Why or why not? (No, the numbers are too
big.)
A Variety of Strategies. This lesson encourages the use of a
variety of strategies. The end goal is not to guide all students
toward using the compact method. The goal is to expose
students to many different strategies so they can choose
strategies that make sense to them and enable them to find a
correct answer.
Give student pairs a piece of chart paper on which to
display their solution strategies. Make sure all of the
strategies are represented. After they solve the problem,
ask students to display their solution strategies.
See Figure 2.
Ask questions that make connections
between the strategies such as:
- How did [student names] show 400? 10? 6?
- How did [student names] show 700? 90? 5?
- How did [student names] show 416 in expanded
form? (400 + 10 + 6)
- On the number line? (4 hops of 100, 1 hop of 10,
and 6 hops of 1)
- Did [student names] make any trades with base
ten pieces? (They traded 10 bits for 1 skinny and
10 flats for 1 pack.)
- What does the pack represent? (1000)
- [Student names] used the compact method. What
do the little 1s above the columns mean? (The little
1s show the trades.)
- How did [student names] show that they were
adding the numbers together?
- Did everyone get the same answer? (yes, 1211)
- Look at the sum, 1211. What is the value of this
1 [thousands column]? (1000) The value of the
1 in this [tens] column? (10) (10) The 2? (200) This
1 [ones column]? (1)
- Does 1000 + 200 + 10 + 1 = 1211? (yes)
- Why does the digit 1 represent one thousand, ten,
and one in 1211? (The value of the digit depends
on where it is placed within the number.)
- How do the answers compare to your estimate?
- Does one way seem more efficient than another
when you are adding larger numbers? Why? (Possible responses: I don't always have base-ten
pieces, so that's not always an efficient strategy.
The paper-and-pencil methods seem more efficient.
The compact method takes less writing
than expanded form and all-partials because
some of the trading steps are kept "in my head"
and not written down, but I have to be careful
because I have to make trades in the middle
instead of waiting until the end. It's not efficient
if I get the wrong answer.)
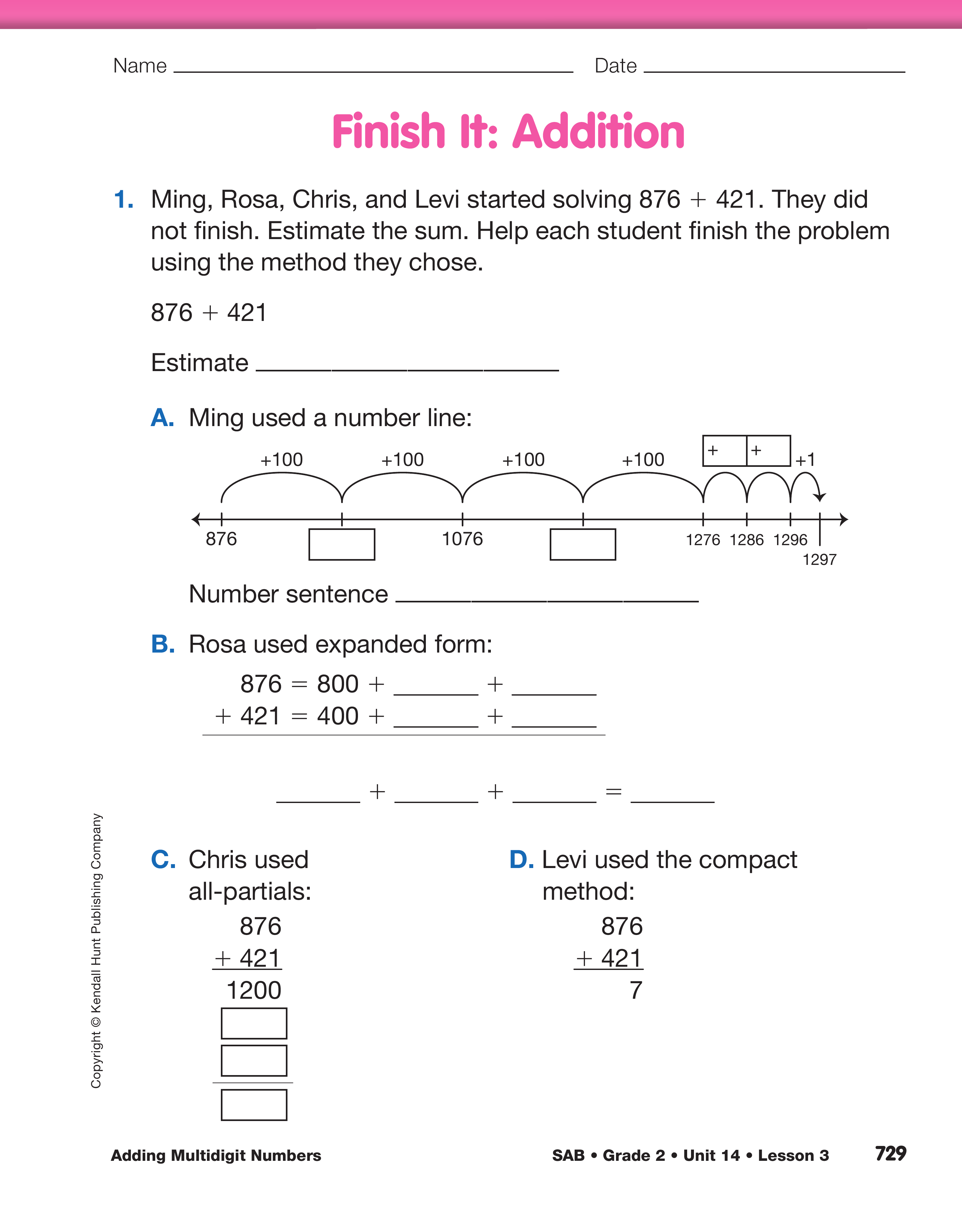
Finish It. Assign the Finish It: Addition pages in the
Student Activity Book. Students will practice using a
variety of methods to solve 3-digit addition problems
and make connections among the strategies.
Upon completion, use the following prompts to discuss
students' work:
- How did you estimate the sum of 876 + 421? (Possible response: I thought about money. 876 is
about $8.75 and 421 is about $4.25. I put 4 quarters
together to make $1.00. I added $1.00 to
$8.00 and $4.00 to get $13.00, so I estimated the
sum to be about 1300.)
- Model the problem with base-ten pieces and solve
it. (1297) [See Figure 3.]
- How does this answer compare to your estimate?
Is your answer reasonable?
- What is 7 tens plus 2 tens? (9 tens)
- How many hundreds did you add together? (8 hundreds plus 4 hundreds)
- How many flats make one pack? (10 flats)
- How many hundreds are in one thousand? (10 hundreds)
- Did you make any trades? (Yes. I had 12 flats so I
traded 10 flats for 1 pack and had 2 flats left
over.)
- Look at the number 1297. Which base-ten pieces
represent the 2? (2 flats) How many hundreds is
that? (2 hundreds)
- Which base-ten pieces represent the 9? (9 skinnies) How many tens is that? (9 tens) What is
another way of saying 9 tens? (90)
- Which base-ten pieces represent the 7? (7 bits) The 1? (1 pack)
- How many bits are in one pack? (1000)

Use Check-In: Questions 2–6 and the Feedback Box on the
Finish It: Addition pages in the Student Activity Book to
assess students' abilities to use and apply place value
concepts to make connections among representations of
multidigit numbers [E1]; add multidigit numbers using
mental math strategies [E6]; add multidigit numbers using
paper-and-pencil methods [E7]; check for reasonableness
[MPE3]; and check calculations [MPE4].