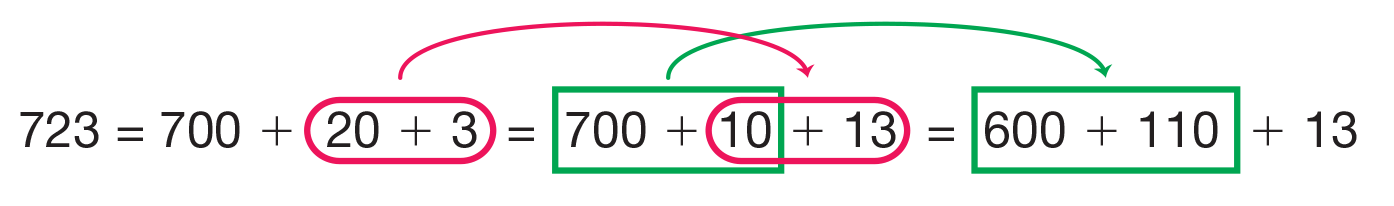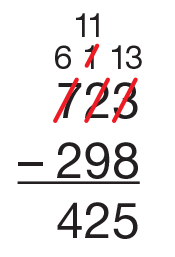Workshop: Multidigit Addition and Subtraction

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Multidigit Addition Strategies

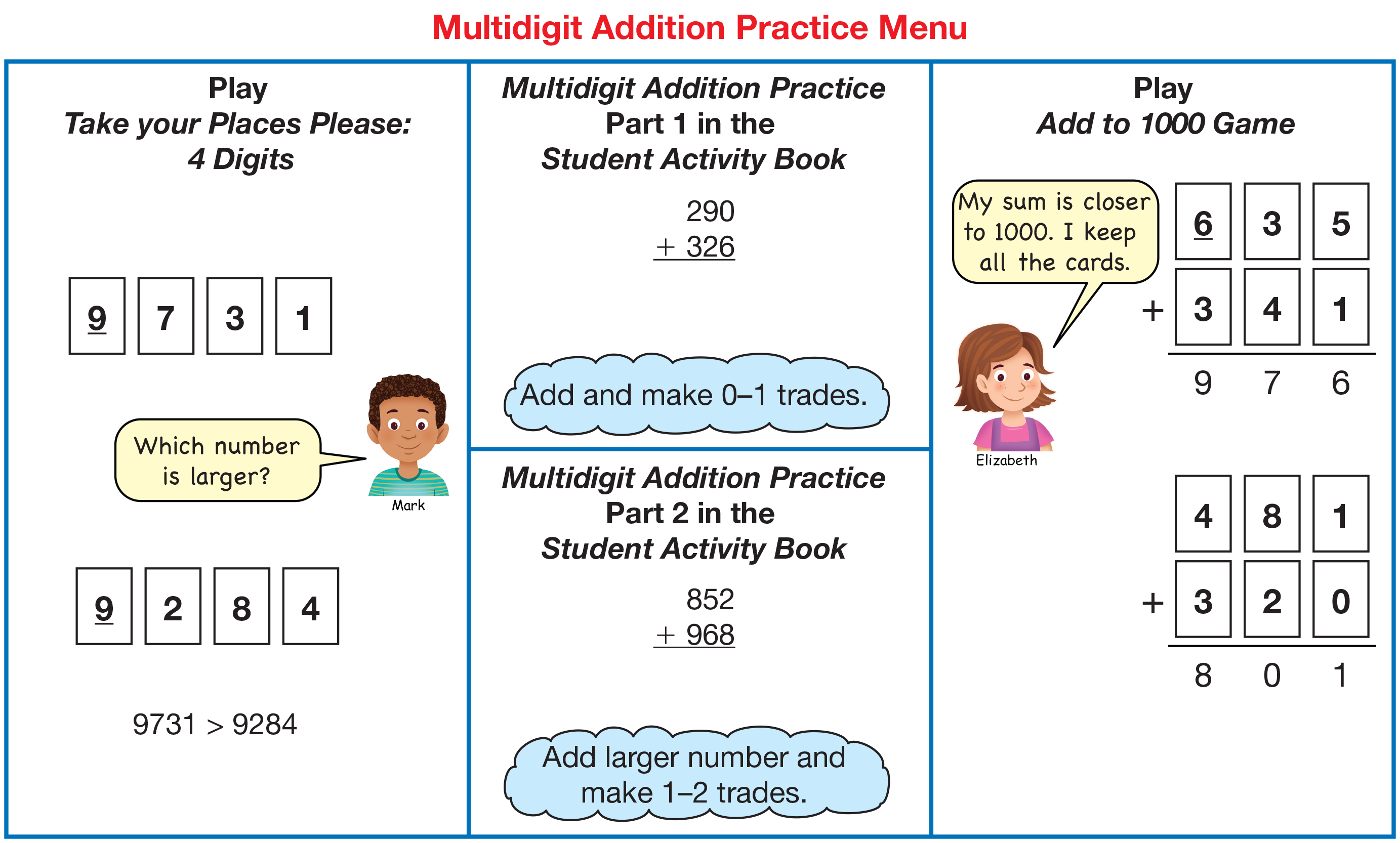
Introduce Addition Practice Menu. Display and direct students' attention to the Multidigit Addition Practice Menu page in the Student Activity Book. See Figure 1. Tell students to tear out the menu as it will help guide them to appropriate practice. Students will do one activity from each column of the menu. Briefly introduce the selections in each column.

A Workshop Menu is a flexible way for students to find the practice and support they need. Monitor and guide students' choices. If students find a particular activity too easy or too difficult, they can simply choose a different activity. Students should work on the activities in this Workshop with another student or with a group of students. Keep these student groups flexible as well.

Introduce and Play Take Your Places Please. The game Take Your Places Please: 4 Digits is offered in the first column. Everyone will play this game. Students played Take Your Places Please in Unit 6. In this game only, each student will use only one set of digit cards. Guide the students as they pull the ten cards with digits 0–9 out of their larger decks as you do the same. Have them set the remaining cards aside for later.

Display and review the directions for the new version of the game on the Take Your Places Please: 4 Digits pages in the Student Activity Book. Introduce the game by explaining that for each round, a player's goal is to make a larger (or smaller) 4-digit number than his or her partner's number.

Next, display the Take Your Places Please 4-Digit Mat. Demonstrate how the leader will draw a digit card. Both players will place the card with that digit in any one of the boxes on their own digit mat. Once they place a digit, it cannot be moved; however, players may choose to discard one card during each round.

As you demonstrate the game, ask:

What is the value of this digit in the number? (Example response: If the number 8 was drawn and placed in the thousands place it means 8000.)
Why did we decide to discard this number? (Possible response: It is a low digit and we were trying to make the largest number.)

Players repeat this process until they have made a 4-digit number.

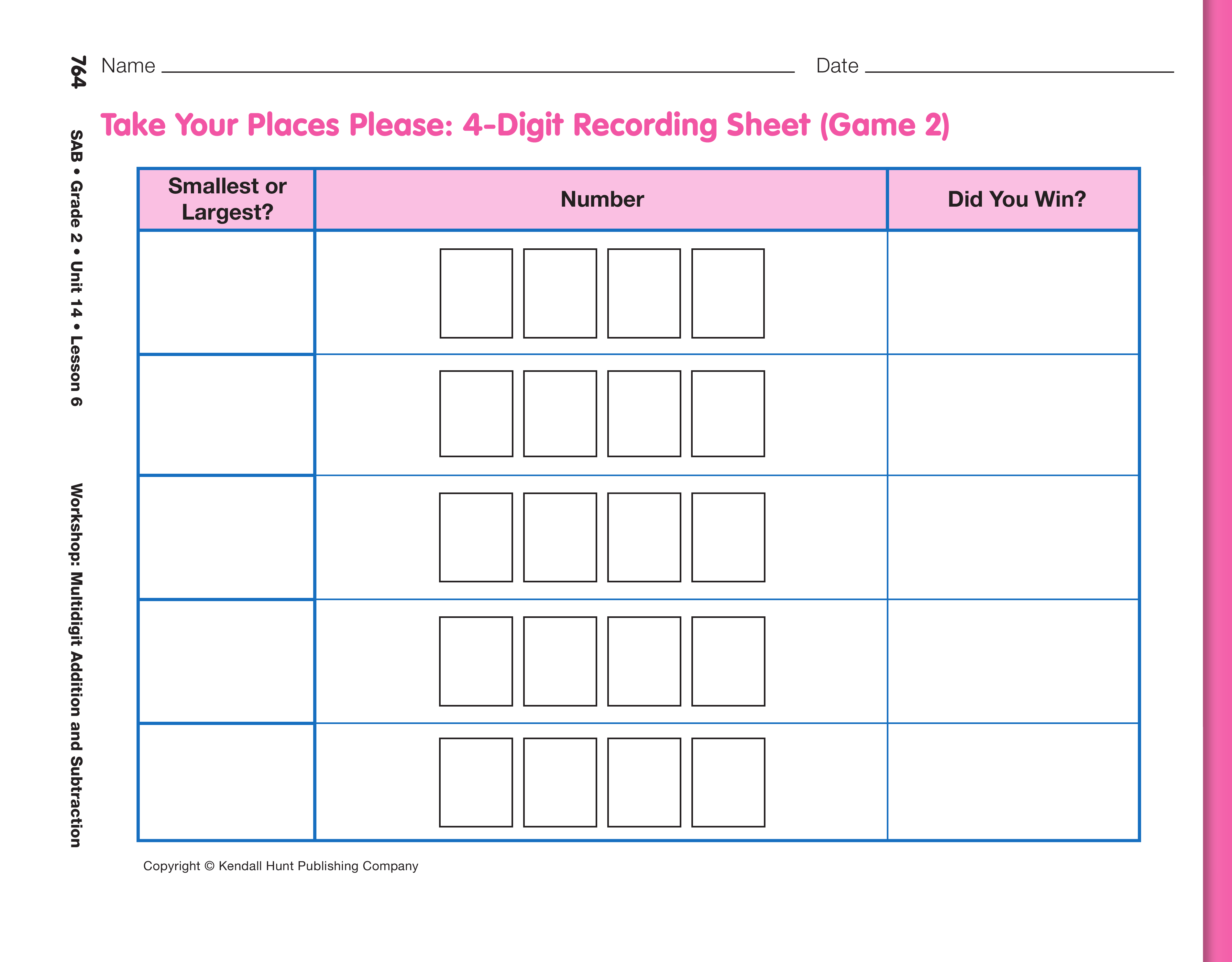
Display the Take Your Places Please: 4-Digit Recording Sheet and show how to record the round. Players compare the numbers to complete the round.

Ask:

Do you think this is a large number?
If you could rearrange the digits, could you make a number larger than this number? (Possible response for the number 8243: yes, 8432)

Organize students into pairs to play the game. The game lasts 5 rounds. Recording Sheets for two games are provided if some student pairs are able to go on to a second game in the time allotted. Ask students to store the digit cards with the rest of the deck in an envelope for future games.

For Take Your Places Please: 4 Digits game, adjust the set of digit cards students use or the number of students who play together based on students' need.

Students could potentially create numbers as large as 9876. Base-ten pieces and base-ten shorthand are available to support students with trading and comparing numbers. A few students may still be depending on actual base-ten pieces for creating their representations. For these students it may be beneficial to work with smaller numbers. Replace each set of 0–9 digit cards with two sets of 0–4 digit cards. The largest number students can create with the 0–4 digit cards is 4433.
This game becomes more challenging if students play with more players. For students ready for a little more challenge, organize them into groups of 3 or 4 students.

After students have had the opportunity to play at least 5 rounds, reconvene as a group and ask:

Let's say you drew a 9 and wanted to make a large number. How did you decide where to place the 9? (Possible response: I wanted to make a big number. I knew if I put the 9 in the thousands place it would be 9000. If I put it in the ones place, it would only be 9.)
Let's say you drew a 2. Where would be the best place to place it and why? (Possible response: I would put it in the ones place to be 2 or the tens place to be 20. Since it is a little number, I would not put it in the thousands place. I would put a bigger number in the thousands place.)
How would this strategy change if you were trying to make the smallest number? (Possible response: I would try to put the smallest number, like a 1 or 2, in the thousands place.)
How does where you place a number change its value? (Possible response: For example, if I put a 7 in the tens place, it is 7 tens. If I put the 7 in the hundreds place, it is 700.)
How did you compare numbers? (Possible response: I looked at the digits in the thousands place first. Whichever number had the most thousands was the larger number. If the numbers in the thousands place matched, I compared the numbers in the hundreds place.)

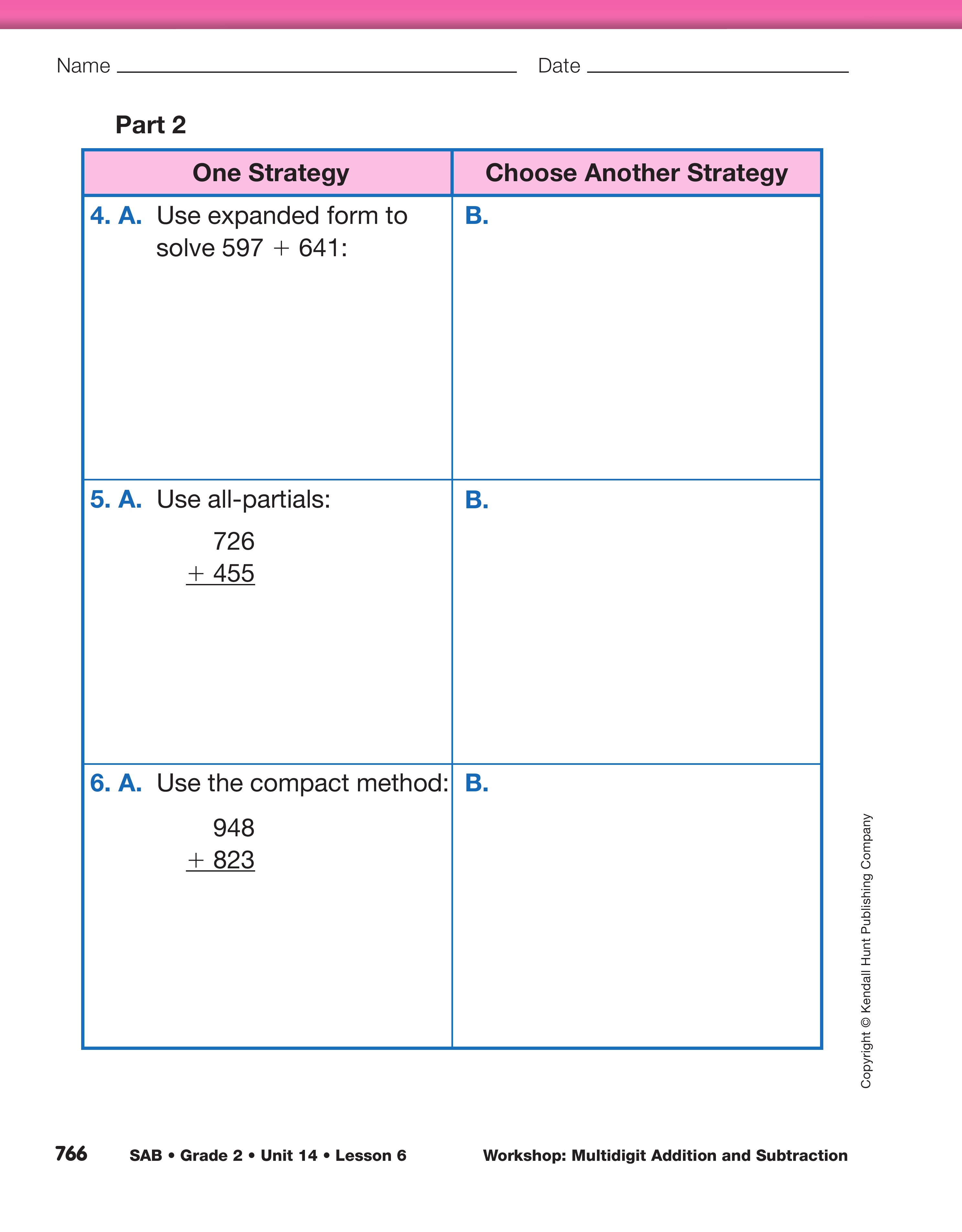
Choose Multidigit Addition Practice. Display the following two problems and ask students to first estimate the sums for each one:

290 852
+ 326+ 968

Direct students' attention back to the Multidigit Addition Practice Menu. These problems are listed in the second column on the menu. Ask students to solve them any way they choose. See Figures 2 and 3 for possible solution strategies. Students may refer to the Addition Strategies Menu in the Student Activity Book Reference section. Have base-ten pieces available.

After they have completed the problems, ask questions such as the following:

Compare your estimate to your answer. Does your sum seem reasonable?
Who used a mental math strategy? For which problem? [See Content Note.]
Did anyone use a number line? Base-ten pieces or shorthand? Show us how.
Who used a paper-and-pencil strategy? For which problem?
Who used expanded form? All-partials? Compact method? Show us how.

Mental Math. Students should have opportunities to develop strategies that make sense to them. Mental math strategies are not necessarily strategies completely done in your head or without support from a tool (e.g., number line, base-ten shorthand, etc.) With practice, students will be able to recall a mental image of these tools to support their thinking. Mental math strategies are those that ask students to think about the numbers they are using and find partitions that can be worked with easily.

For example:402 + 568 = 400 + 2 + 568
= 400 + 570
= 970

The problems in Part 1 of the Multidigit Addition Practice pages in the Student Activity Book provide problems with 0–1 trades, such as 290 + 326 and have a little more scaffolding. Those in Part 2 provide problems similar to 852 + 968 with 1–2 trades and involve larger numbers.

Ask the following questions to help students choose their practice:

How confident are you in your answers?
Did you need any tools to help you?
Did you solve both problems easily?
Which set of problems do you think you should choose for practice?

Tell students to circle one activity, Multidigit Addition Practice Part 1 or Part 2, from the second column of the Multidigit Addition Practice Menu.

Students use the Multidigit Addition Practice Menu to self-assess their abilities to add multidigit numbers using mental math strategies [E6] and paper-and-pencil methods (e.g., expanded form, all-partials, compact) [E7].

Introduce Add to 1000 Game. The third column on the Multidigit Addition Practice Menu lists the Add to 1000 Game. Everyone will play this game. Students played Add to 100 in Unit 7. Introduce the new version of the game by displaying the Add to 1000 Game page from the Student Activity Book. You will need the display deck of digit cards that you prepared prior to the lesson. Read the directions to the game aloud. Shuffle the cards and ask a student to volunteer to play a demonstration game with you. Each player uses 6 cards to make an addition problem. The player whose answer is closest to 1000 takes all the cards. Explain to students that sums can be more than or less than 1000 and that they will need to determine which player's sum is closest to 1000. The player with the most cards at the end of the game wins.

Practice Multidigit Addition and Play Add to 1000 Game. When students are ready with their tasks, ask them to begin working. Remind students that they can refer to the Addition Strategies Menu in the Student Activity Book Reference section as they work on problems and play the game. Have tools such as base-ten pieces readily available. As students complete the problems on the Multidigit Addition Practice pages, they can find a partner and play the Add to 1000 Game. Alternatively, you may assign partners and decide to have the entire class move on to the game when most students have completed the Multidigit Addition Practice pages.

Unfinished problems in either Part 1 or Part 2 of the Multidigit Addition Practice pages in the Student Activity Book may be assigned as homework. Have students store the digit cards in an envelope for use in Part 2 of the Workshop.

The Addition Strategies Menu and the Subtraction Strategies Menu for Larger Numbers are designed to help students choose different, appropriate, and efficient strategies. They also allow you to help students focus on certain strategies and not others, if you choose. For students struggling with addition, have them focus on the all-partials method or using expanded form. For students struggling with subtraction, expanded form is a more transparent strategy that can help them better understand regrouping. For students who are confident with addition and subtraction, ask them to try using some mental math strategies and to focus on finding efficient strategies for each problem.

Adventure Book: