Subtract with Mental Math

Est. Class Sessions: 2

Developing the Lesson

Part 1: Using Estimation Strategies

Review Estimation Strategies for Addition Chart. Use the Estimation Strategies for Addition chart to review the strategies students developed for estimating sums in Lesson 2 of this unit:

Using Friendly Numbers (Closest 100)
Using Friendly Numbers (Closest 10)
Thinking about Base-Ten Pieces
Counting On by Hundreds and Tens
Adding Hundreds
Composing and Decomposing Numbers

Explain to students that they will be using similar strategies for estimating differences.

Ask:

Will these strategies also work for subtraction problems? (Possible response: Probably, but we have to change some strategies because we're subtracting.)
What strategies could we change? (Possible response: We have to change "Adding Hundreds" to "Subtracting Hundreds." We could add "Counting Back by Hundreds and Tens.")

Modify the estimation strategies and write them on the new Estimation Strategies for Subtraction chart you prepared prior to the lesson. See Materials Preparation.

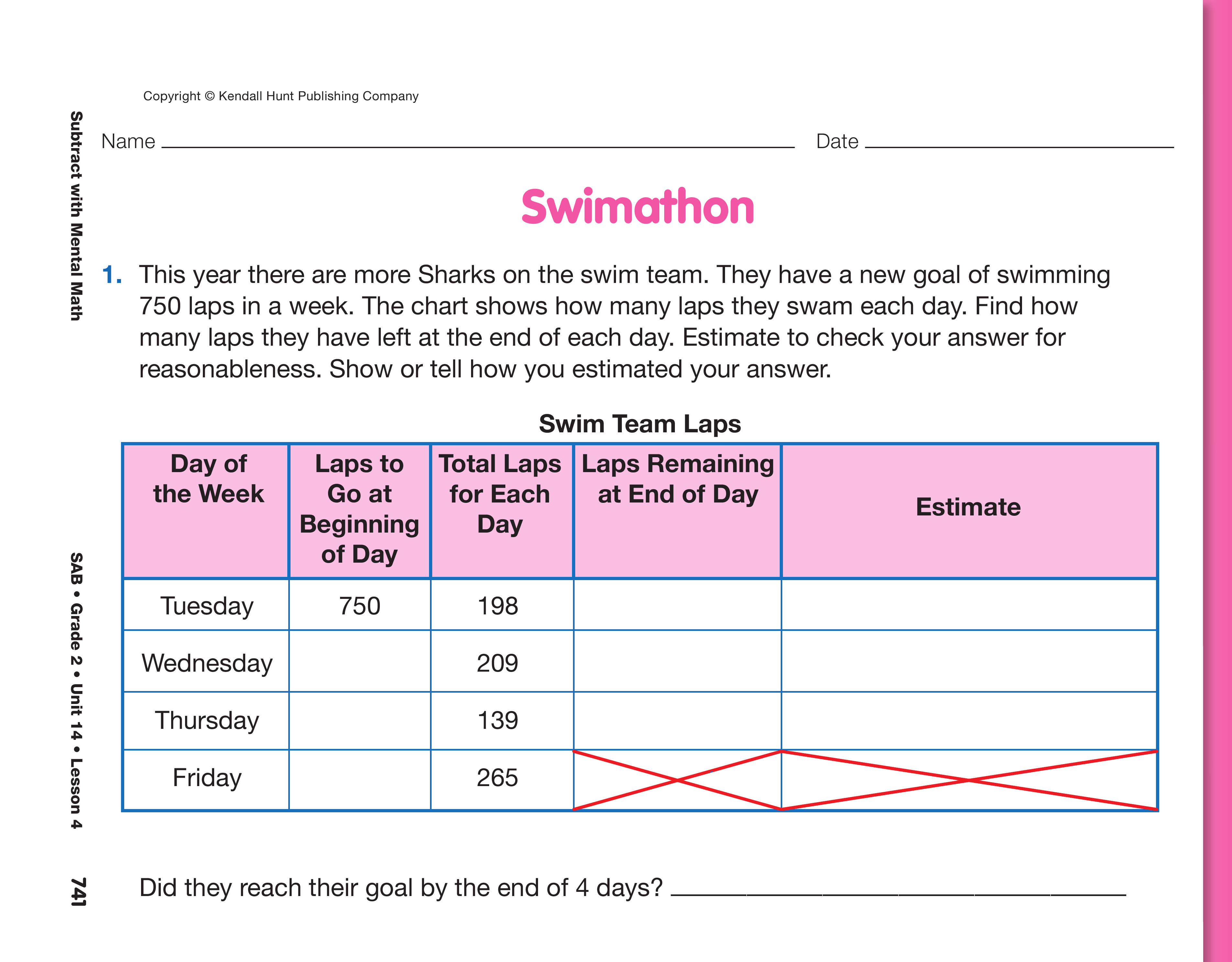
Read Shark Swimathon. Use the book Shark Swimathon to review estimating differences for two-digit numbers. Shark Swimathon is a story about a group of sharks that have to swim 75 laps by the end of the week. Each day, they subtract the total number of laps they swam from the total number remaining. As you read the story, have students estimate the reasonableness of each difference.

Ask questions such as the following:

The sharks had to swim 75 laps. After the first day they swam 14 laps. Flap said they had 61 left to swim. Is that a reasonable answer? (Possible response: Yes, because 14 is close to 15 and 75 − 15 = 60. Sixty is close to 61.)
On Wednesday, they had 61 laps left to go and they swam 17. About how many laps did they have left? (Possible response: They had about 45 laps left. I found friendly numbers for 61 and 17: 60 − 15. Sixty minus 10 is 50 and 5 more is 45. My estimate is 45.)

Show students the actual answer is 44.

On Thursday, Coach Blue subtracted 19 from 44. How can you tell quickly that 25 is a reasonable answer? (Possible response: If I subtract 20 from 44, the answer is 24, so 19 from 44 should be 25.)
On Friday, they had 25 laps left to swim but Gill had an accident. There were 5 sharks left and 25 laps to go. How many laps would each shark have to swim to reach 25? How do you know? (5; Possible response: I knew 2 laps for each shark would only be 10 laps and 10 laps for each shark would be 10, 20, 30, 40, 50—too many. So I tried 5. If each shark swam 5 laps, that would be 5, 10, 15, 20, 25 laps.)

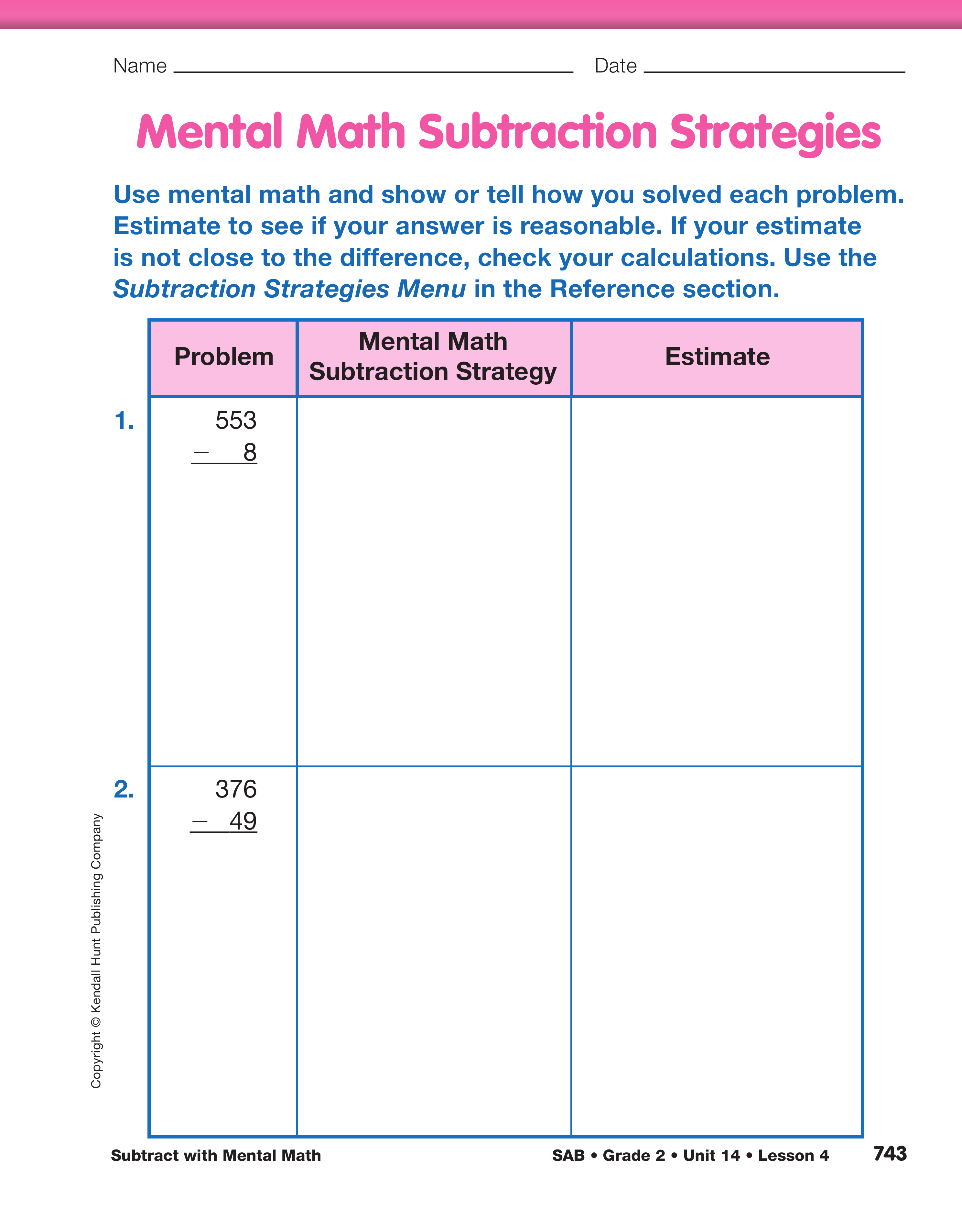
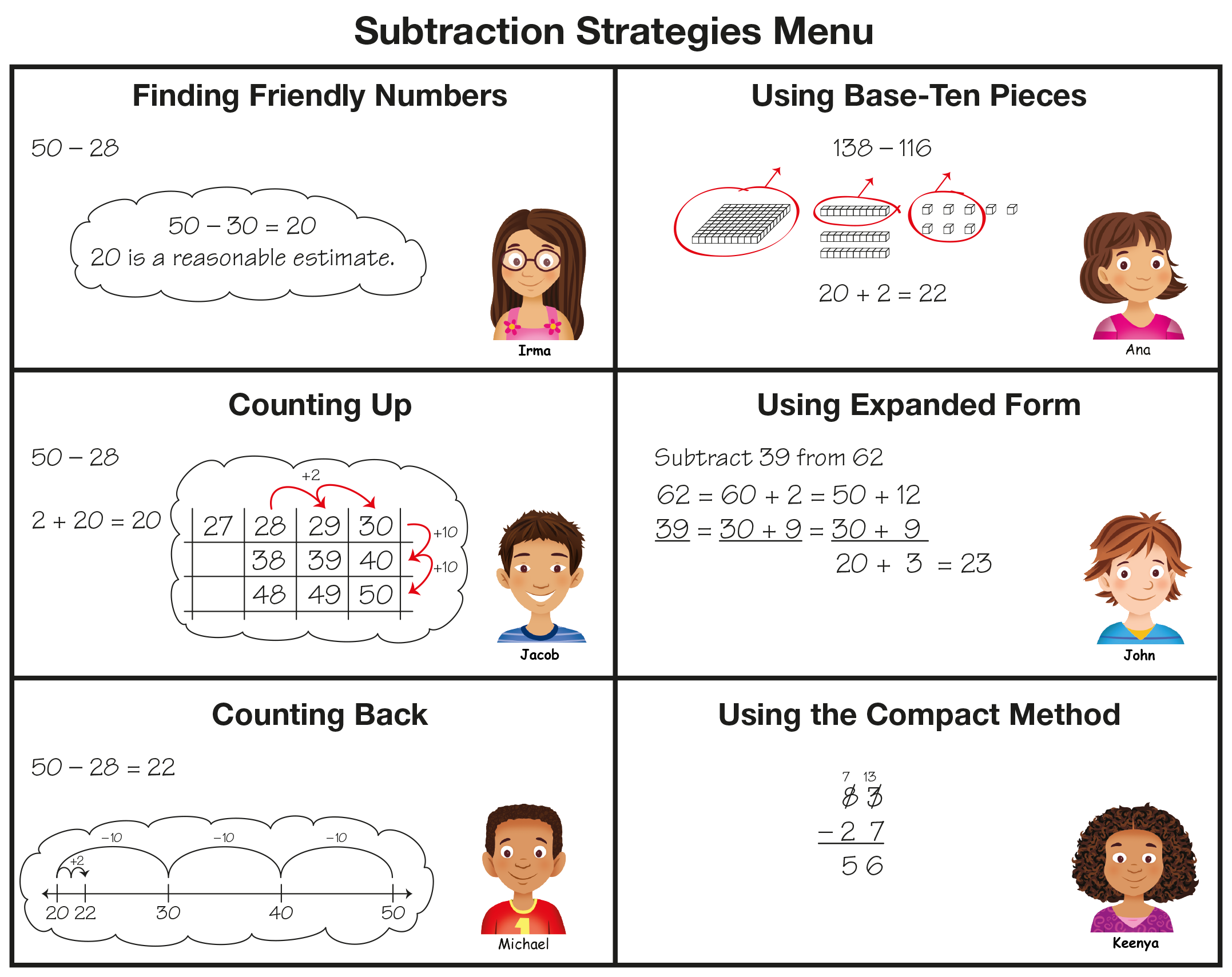
Find Differences and Estimate for Reasonableness. Use the display of the Swimathon page in the Student Activity Book to introduce the activity. For Question 1, ask student pairs to find how many laps the sharks had left to swim at the end of each day and to check their answers for reasonableness by estimating the differences. Encourage students to refer to the Subtraction Strategies Menu in the Student Activity Book Reference section and to use what they know about subtracting two-digit numbers to solve the subtraction problems with three-digit numbers on the chart. See the Content Note. Have the Estimation Strategies for Subtraction chart, the Subtraction Strategies Menu, open number lines, and base-ten pieces readily available.

Learning Progression. In the next lesson of this unit, students will make connections between various paper-and-pencil methods and mental math strategies for subtracting three-digit numbers. For the Swimathon page, allow students to build on what they know about subtracting two-digit numbers and develop different ways of subtracting multidigit numbers that make sense to them. This will help students develop a deeper understanding of various paper-and-pencil methods before they are formally introduced.

Circulate around the room and observe students as they develop strategies for finding the difference and estimating for reasonableness. Look for interesting strategies that students can demonstrate to the class.

Upon completion, have student pairs share their strategies.

Ask:

How did you find how many laps the sharks had at the end of each day?

See Figure 1 for possible strategies for finding the differences on the Swimathon page.

If they only had 204 laps to go on Friday morning, how many did they swim over their goal? (61 laps)
How did you know? (Possible response: I started at 204 and counted up by tens: 214, 224, 234, 244, 254, 264. That's 6 tens or 60 and 1 more makes 265. The answer is 61 laps over the goal.)

Use the display of the Swimathon page in the Student Activity Book to fill in the chart and discuss estimation strategies.

What estimation strategies did you use to check your answers to make sure they were reasonable?

See Figure 3 for possible estimation strategies.

Add the estimation strategies students used for the Swimathon page to the Estimation Strategies for Subtraction chart. In Figure 3, some of the strategies used were:

Using Friendly Numbers (nearest hundred)
Using Friendly Numbers (changing only one number, usually the number to be subtracted)
Using Friendly Numbers (nearest ten)
Subtracting Hundreds
Counting Back on the Number Line
Thinking about Base-Ten Pieces

As a class, discuss why students have different estimates.

Ask:

Did everyone get the same estimate? Why or why not? (no; Possible response: Maybe we used different strategies so we didn't get the same answer.)
When you compare your estimates to someone else's estimates, were they close even though the strategies were not the same? (Possible response: They were close.)

After discussing the estimation strategies students used for Question 1 on the Swimathon page in the Student Activity Book, ask student pairs to estimate the answers for Questions 2–4. Have the Estimation Strategies for Subtraction chart, open number lines, and base-ten pieces readily available.

Check for Reasonableness. Encourage students to use estimation strategies that rely on their understanding of place value and that make sense to them. Focus on using mental math to check for reasonableness of a difference. Although finding the closest ten or hundred for a number is one of the strategies mentioned in this lesson, mastery of this concept is not expected at this level.

Adventure Book:

Student Activity Book: 741 742 743

Answers